Презентація "Задачі для усного рахунку. Трапеція"
Про матеріал
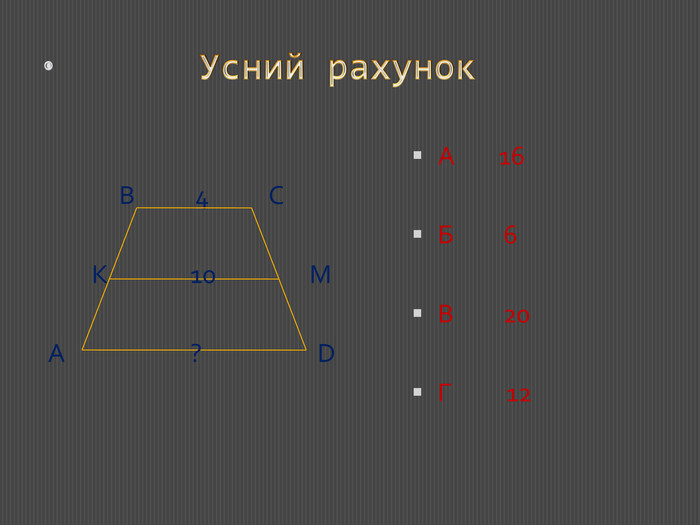
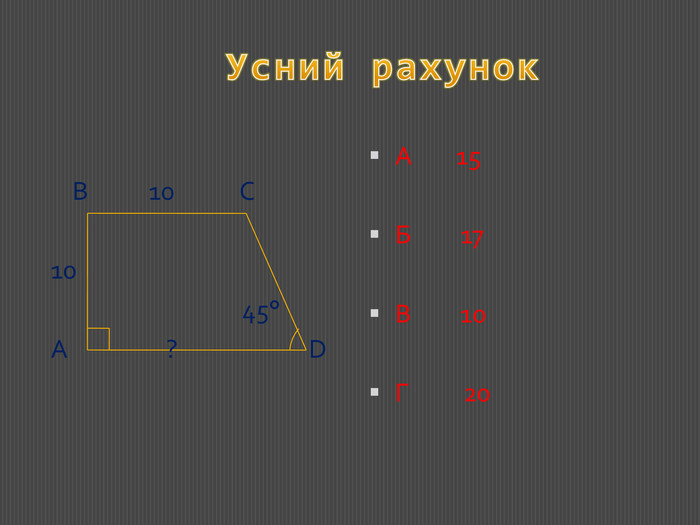
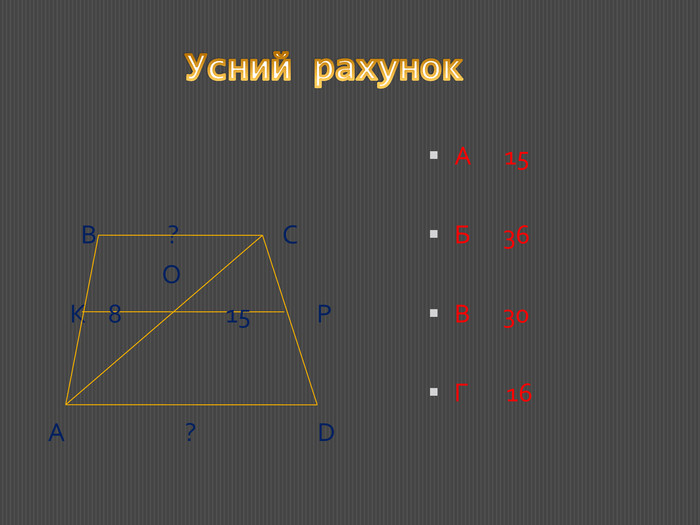
В основному, завдання репродуктивного характеру на 1-2 логічних кроки і представлені у формі тестівз вибором однієї правильної відповіді. Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку