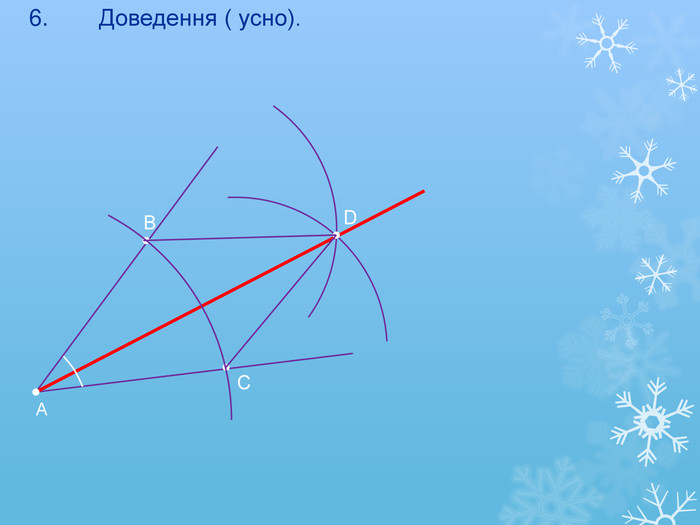
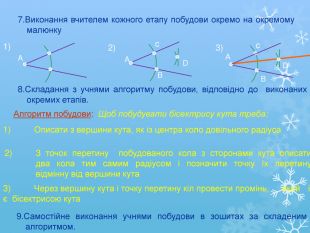
Презентація ,,Задачі на побудову''
Про матеріал
До вашої уваги пропонується короткий виклад змісту дипломної роботи, яка виконана на тему “ : Задачі на побудову в курсі геометрії основної школи та методика їх розв’язування”.
Актуальність теми. Геометричні побудови є істотним чинником математичної освіти; вони являють собою потужне знаряддя геометричних досліджень. Теорія геометричних побудов становить теоретичну основу практичної графіки: багато креслярських методів опираються на розв'язки геометричних задач на побудову.
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку