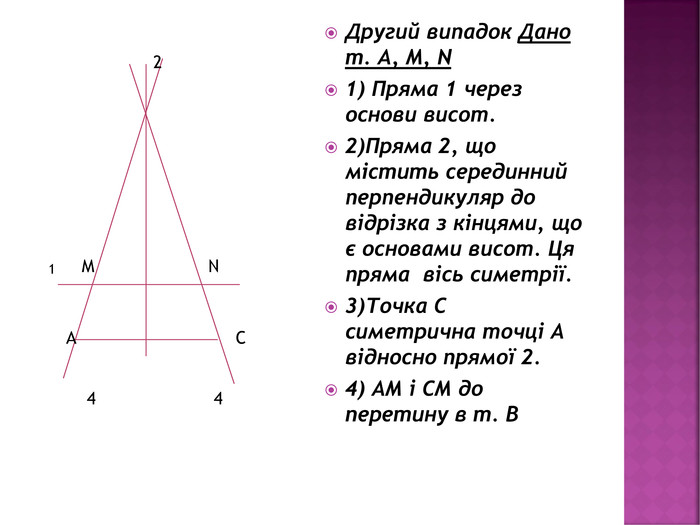
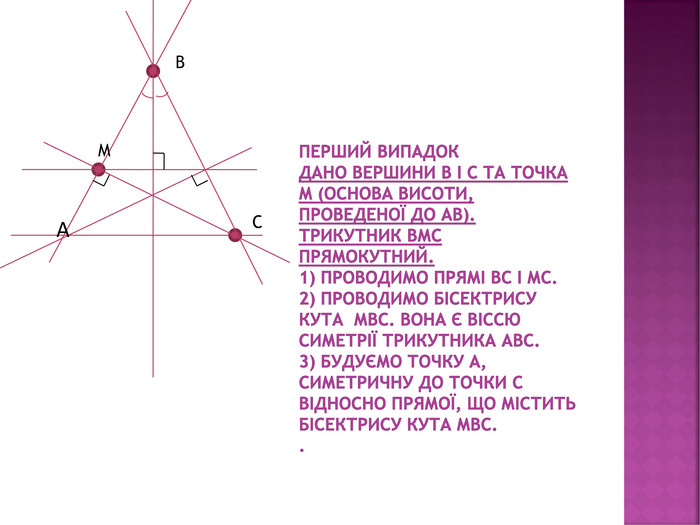
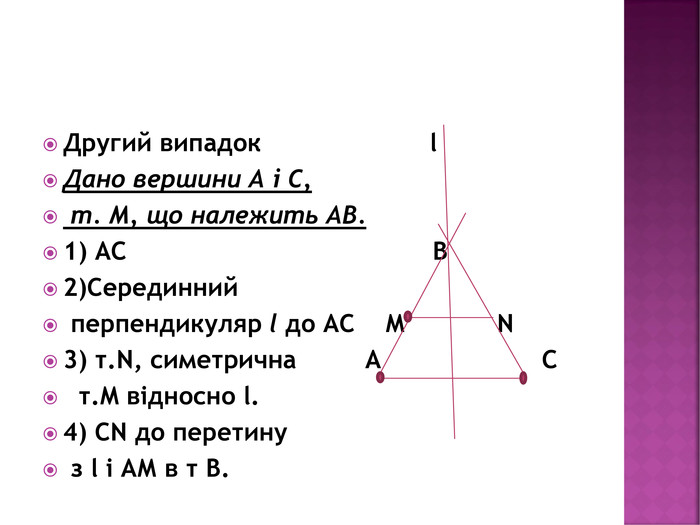
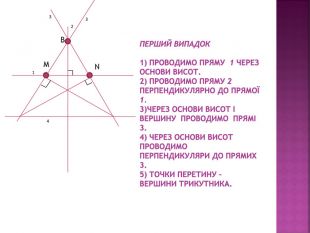
Презентація "Задачі на відновлення фігур"
Про матеріал
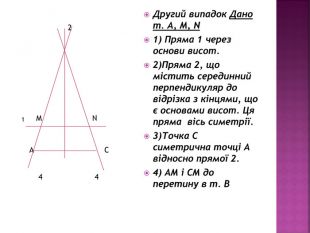
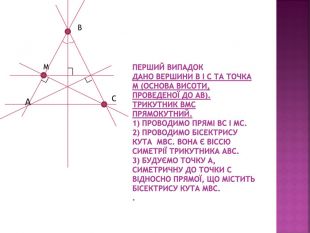
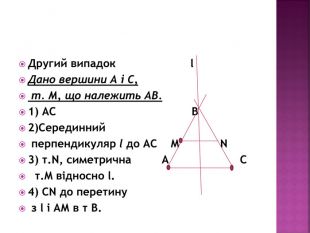
Ще одна презентація до теми "Рухи" у 9 класі. Розглянуто цікаві задачі на відновлення фігур. Презентували ці задачі 9-класники. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку