Урок "Розв'язування трикутників. Прикладні задачі."

Тема уроку: Розв’язування  трикутників. Прикладні задачі.

Мета уроку: узагальнити та систематизувати знання учнів з теми: «Розв’язування трикутників», закріпити вміння та навички розв’язування трикутників; формувати вміння застосовувати набуті знання  до розв’язування прикладних задач; розвивати пізнавальну активність учнів, логічне мислення, уяву; виховувати самостійність, наполегливість, впевненість у собі, інтерес до вивчення геометрії.

Серед рівних розумом – за однакових інших умов – переважає той, хто знає геометрію.

Блез Паскаль

Хід уроку

І.Організаційний момент.

ІІ. Повідомлення теми і мети уроку.   Мотивація навчальної діяльності.

Учитель.

Трикутник. Ця геометрична фігура знайома вам  починаючи з 7 класу, з уроків геометрії. Вона містить в собі чимало цікавого та загадкового, як Бермудський трикутник, в якому безслідно зникають кораблі та літаки. Знайомі вам також геометричні фігури - квадрат, паралелограм, прямокутник, ромб, трапеція. Але якщо провести одну діагональ , то всі вони складаються з трикутників,.

На попередніх уроках ми розглянули  теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників, розглянули основні типи задач на обчислення елементів довільних трикутників.

Сьогодні  перед нами стоїть задача:

• повторити все, що вивчили;
• пригадати те, що забули;
• вміло застосовувати отримані знання до розв’язування геометричних задач.

Але перш, ніж ми почнемо,  я прошу звернути вашу увагу рекомендації до нашого уроку. Якщо ви будете слідувати їм, то я впевнена, що сьогодні на уроці ви обов’язково виконаєте всі завдання тільки на високому рівні.

Рекомендації до уроку:

• Будь уважним.
• Міркуй, шукай, порівнюй, роби висновки, працюй.
• Шукай нові способи розв’язування проблеми.
• Самостійно встановлюй зв’язки відомого з невідомим.
• Будь упевнений у своїх здібностях.

Недостатньо мати добрий розум .

Головне - раціонально застосовувати його.  

Р. Декарт

Математика застосовується абсолютно скрізь. Зараз математика застосовується не тільки в астрономії, механіці, фізиці, хімії і техніці, де вона застосовувалася і раніше, але також – у біології, суспільних науках і навіть у мовознавстві. Математики передбачають погоду, обчислюють орбіти штучних супутників, курси кораблів, перекладають наукові тексти з однієї мови на іншу.

Знання стають міцнішими, якщо вони застосовуються у практичній діяльності.

Тому проведемо урок практичного застосування знань, що ви отримали під час вивчення теми «Розв’язування трикутників» і ви дізнаєтеся як можна застосувати знання даної теми в житті.

Але спочатку давайте повторимо все, що ми вивчили по даній темі.

ІІІ. Актуалізація опорних знань

1.Запитання до класу:     

1. Яку фігуру називають трикутником?
2. Назвіть основні елементи трикутника.
3. Які види трикутників за кутами ви знаєте?
4. Які види трикутників за сторонами ви знаєте?
5. Як називається сторони в рівнобедреному трикутнику?
6. Що називається синусом кута (косинусом)?
7. Що означає розв’язати трикутник?
8. Сформулювати теорему косинусів.
9. Теорема синусів.
10.                    Наслідок з теореми синусів. (радіус кола, описаного навколо тр-ка =  половині відношення сторони до синуса протилежного кута)

2. Усні вправи (learning)

В геометрії для розв’язування задач ми використовуємо багато формул, які доводяться за допомогою теореми синуса, або косинуса. Нагадайте мені формули для знаходження площі трикутника.

Задача 1.

Вивести формулу Герона для площі трикутника.

Розв’язання.

Як відомо:   a²   = b²    + c²  - 2bc cos α;     S=

Отже:                           

Підставимо знайдені вирази в формулу sin²α + cos²α = 1

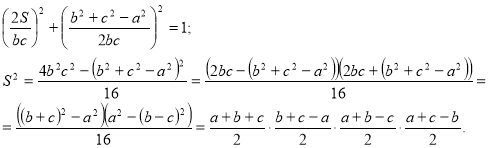
Оскільки:

Маємо: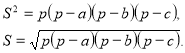  

Що і треба було довести.

Розв’язування трикутників широко застосовується на практиці, зокрема під час проведення вимірювань на місцевості. Вміти розв’язувати трикутники потрібно для того, щоб визначити відстані, не вимірюючи їх безпосередньо. Кути на місцевості вимірюють спеціальними приладами. (Слайд)

Перша задача, яку ми розглянемо

Задача 1. Знайдіть відстань від пункту А до недоступного пункту В.

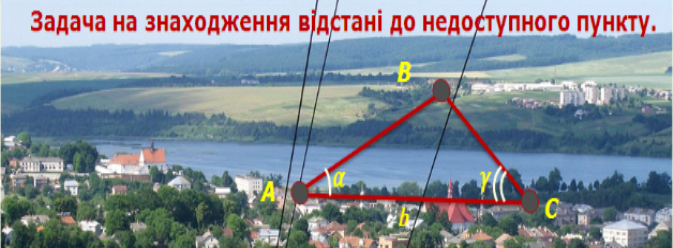
 Розв’язок даної  задачі демонструється поетапно на екрані, вчитель пояснює  учням кожен крок розв’язання, при цьому, використовує елементи бесіди.

 Розв’язання. Обираємо на місцевості таку точку С, щоб з неї було видно пункт В і можна було виміряти відстань АС. Вимірюємо АС. Потім за допомогою спеціальних приладів для вимірювання кутів на місцевості визначаємо градусні міри кутів ∠BАС і ∠ BСA. Отже, нехай АС =b,  ∠BАС=