Приклади розв"язування задач з астрономії

Приклади розв’язання задач з астрономії

§ 1. Зоря Вега розташована на відстані 26,4 св. року від Землі. Скільки років летіла б до неї ракета з постійною швидкістю 30 км/с?

Швидкість ракети в 10 0 0 0 разів менша, ніж швидкість світла, тому космонавти будуть летіти до Беги у 10000 разів довше.

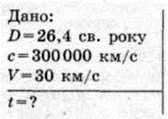
Розв’язання:

§ 2. Опівдні ваша тінь у два рази менша, ніж ваш зріст. Визначте висоту Сонця над горизонтом.

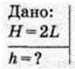
Розв’язання:

Висота Сонця h вимірюється кутом між площиною горизонту та напрямком на світило. З прямокутного трикутника, де катетами є L (довжина тіні) та Н (ваш зріст), знаходимо

§ 3. На скільки відрізняється місцевий час у Сімферополі від київського часу?

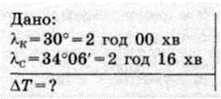
Розв’язання:

Взимку 

Тобто взимку місцевий час у Сімферополі випереджає київський час. Весною стрілки всіх годинників у Європі переводять на 1 год вперед, тому київський час випереджає на 44 хв місцевий час у Сімферополі.

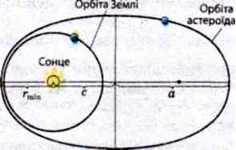
§ 4. Астероїд Амур рухається по еліпсу з ексцентриситетом 0,43. Чи може цей астероїд зіткнутися із Землею, якщо його період обертання навколо Сонця дорівнює 2,66 року?

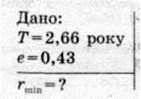
Розв’язання:

Астероїд може зустрітися із Землею, якщо він перетнеться з орбітою Землі, тобто якщо відстань у перигелії rmin= < 1 а. o.

За допомогою третього закону Кеплера визначаємо велику піввісь орбіти астероїда:

Де a2- 1 а. o.- велика піввісь орбіти Землі;T2 = 1 рік – період

Обертання Землі :

2.

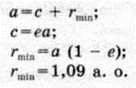
Відповідь.

Астероїд Амур не перетне орбіту Землі, тому не може зіткнутися із Землею.

§ 5. На якій висоті над поверхнею Землі має обертатися геостаціонарний супутник, який висить над однією точкою Землі?

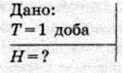
1. За допомогою третього закону Кеплера визначаємо велику піввісь орбіти супутника:

Де а2 = 3 80000 км – велика піввісь орбіти Місяця; 7і, = 1 доба – період обертання супутника навколо Землі; Т”2 = 27,3 доби – період обертання Місяця навколо Землі.

А1 = 41900...

км.

Відповідь. Геостаціонарні супутники обертаються із заходу на схід у площині екватора на висоті 35500 км.

§ 6. Чи можуть космонавти з поверхні Місяця неозброєним оком побачити Чорне море?

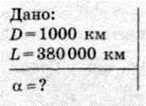
Розв ‘язання :

Визначаємо кут, під яким із Місяця видно Чорне море. З прямокутного трикутника, у якому катетами є відстань до Місяця і діаметр Чорного моря, визначаємо кут:

Відповідь.

Якщо в Україні день, то з Місяця Чорне море можна побачити, бо його кутовий діаметр більший від роздільної здатності ока.

§ 8. На поверхні якої планети земної групи вага космонавтів буде найменшою?

Розв’язання:

P = mg; g=GM/R2,

Де G – гравітаційна стала; М – маса планети, R – радіус планети. Найменша вага буде на поверхні тієї планети, де менше прискорення вільного падіння. З формули g=GM/R визначаємо, що на Меркурії # = 3,78 м/с2 , на Венері # = 8,6 м/с2 , на Марсі # = 3,72 м/с2 , на Землі # = 9,78 м/с2 .

Відповідь.

Вага буде найменшою на Марсі – у 2,6 разу меншою, ніж на Землі.

§ 12. Коли, взимку чи влітку, у вікно вашої квартири опівдні потрапляє більше сонячної енергії? Розгляньте випадки: А. Вікно виходить на південь; Б. Вікно виходить на схід.

Розв’язання:

А. Кількість сонячної енергії, яку отримує одиниця поверхні за одиницю часу, можна обчислити за допомогою такої формули:

E=qcosi

Де q – сонячна стала; і – кут падіння сонячних променів.

Стіна розташована перпендикулярно до горизонту, тому взимку кут падіння сонячних променів буде меншим. Отже, як це не дивно, взимку у вікно вашої квартири від Сонця надходить більше енергії, ніж улітку.

Б. Якщо вікно виходить на схід, то сонячні промені опівдні ніколи не освітлюють вашу кімнату.

§ 13. Визначте радіус зорі Вега, яка випромінює у 55 разів більше енергії, ніж Сонце. Температура поверхні становить 1 1000 К. Який вигляд мала б ця зоря на нашому небі, якби вона світила на місці Сонця?

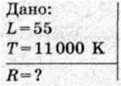
Розв’язання:

Радіус зорі визначають за допомогою формули (13.11):

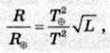
Де Др, = 6 9 5 202 км – радіус Сонця;

– температура поверхні Сонця.

Відповідь.