Проблемне навчання. Обмін досвідом.

Проблемне навчання.

       „Яка радість особливо велика,

коли вдається досягти бажаного”

      Ф. Мілетський

Кожен учитель мріє, щоб його учні зацікавлено працювали, знали і любили його предмет.

Активна розумова діяльність учня – це передумова для формування глибоких та міцних знань і розвитку творчого мислення. Мислення учня активізується, якщо в нього виникає бажання розуміти, вивчати новий матеріал, з’явилась зацікавленість роботою, коли він стає співучасником навчально – пізнавального процесу.

Застосування проблемного навчання дає можливість підняти рівень засвоювання учнями понять, навчити не окремим розумовим операціям в стихійному порядку, а системі розумових дій для розв’язання нестереотипних задач. Активність полягає в тому, що учень аналізуючи, порівнюючи, синтезуючи, узагальнюючи, конкретизуючи фактичний матеріал сам отримує з нього нову інформацію.

Можна виділити такі способи створення проблемних ситуацій:

1) Використання учбових та життєвих ситуацій, які виникають при роботі учнів з практичними завданнями. Проблемні ситуації в цьому випадку виникають при спробі учнів самостійно досягти поставленої мети.

Наприклад у 5 класі при вивченні теми „Додавання десяткових дробів” пропоную виконати усно вправи виду:

а) 0,3+4  б) 0,7+0,1  в) 2,1+3,2

    0,7+2      0,3+0,4               3,4+1,5

    2,3+3      0,6+0,2               0,7+1,2 

Потім виконуємо додавання дробів (із записом на дошці):

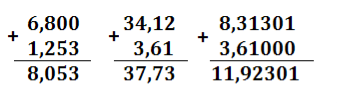
Після виконання дій учні формулюють алгоритм додавання десяткових дробів.

Або у 9 класі при вивчені теми „Довжина кола” пропоную учням дома знайти відношення довжини кола до його діаметра, вимірявши ці величини, використовуючи дно тарілки, чашки, тощо. А на уроці учні роблять висновок про залежність довжини кола до його діаметра, вводиться число . Після цього шукають шляхи розв’язку проблеми і переходять до доведення в загальному вигляді.

У 11 класі при вивчені теми „Логарифм” пропоную учням за допомогою графіка , знайти значення Порівняти значення і , після чого учні роблять висновок, що .

2) Спонукання учнів до теоретичного пояснення явищ, фактів, зовнішньої невідповідності між ними. Це викликає пошукову діяльність учнів.

Алгебра 10 клас тема „Ірраціональні рівняння”. Пропоную учням перевірити чи є х= - 6 коренем рівняння (ні). Далі задаю питання: який спосіб можна застосувати пригадуючи матеріал 8 класу (піднесення двох частин до квадрату). Але це приводить до появи стороннього кореня. Виникає зовнішня невідповідність між фактами, яка приводить до проблемної ситуації.

3) Спонукання учнів до порівняння фактів, явищ, правил, дій внаслідок яких виникає проблемна ситуація.

Наприклад при вивчені в 10 класі теми „Аксіоми стереометрії і способи задання площин” пропоную   такі питання:

а) Як перевірити столяру чи рівні довжини ніжок стільця не використовуючи лінійку?

б) Щоб зачинити двері досить закріпити її в одній точці язичком замка. Чому?

в) Щоб знайти найбільш стійке положення вимірювальних приладів, їх встановлюють на триногах. Чому?

Постає питання: як можна задати площину? Учні самі формулюють проблему і після зіставлення фактів формулюють способи задання площини.

У 8 класі при вивченні теми „Формули коренів квадратного рівняння” даю декілька рівнянь розв’язати шляхом виділення повного квадрата:

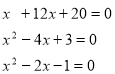
а потім для порівняння розв’язати:

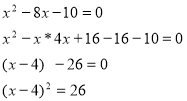
26 – не є квадратом цілого числа і на цьому в учнів виникає проблема. Зрозуміло, що спосіб виділення повного квадрата двочлена універсальний, але громіздкий, тому потрібна формула коренів рівняння.

Значення задач проблемного характеру для досягнення мети навчання математиці переоцінити неможливо. Їх використання забезпечує більш свідоме оволодіння учнями математичної теорії, формує в них навички самостійної роботи й уміння виділяти суттєві властивості математичних об’єктів.

Для створення проблемних ситуацій, задачі повинні бути підібрані так, щоб їх постановка привела до необхідності отримання нових знань, а отримані знання дозволяють розв’язувати не тільки дану, але й інші задачі прикладного характеру.

Наприклад в 9 класі при вивченні теми „Прогресії” можна запропонувати такі задачі:

1) Деякі бактерії, що знаходяться в поживному середовищі, діляться навпіл кожні півгодини. Скільки бактерій утвориться з однієї через 10 годин?

2) Яку суму складатиме банківський вклад 2000грн через 4 роки, якщо він збільшується щороку на 7%?

Учні приходять до висновку, що прогресії застосовуються в різних життєвих ситуаціях.

Постановка перед учнем проблемних ситуацій приводить до того, що він не „пасує” перед проблемами, а намагається їх вирішити.

Проблемні питання містять в собі ще не розкриту проблемну область невідомого, нові знання, для добування яких необхідна якась інтелектуальна дія. Питання вчителя повинно бути складним настільки, щоб примусити учнів замислитись і в той же час посильним для самостійного знаходження відповіді. Тому формування питання логічно повинно бути зв’язаним не тільки з новими, але і з попередніми знаннями.

Наприклад при вивченні теорем стереометрії у 10 класі можна поставити такі проблемні питання

1) Якщо пряма перпендикулярна до двох прямих, які лежать в площині і перетинаються, то вона перпендикулярна до даної площини.

 Проблемні питання:

• Яке слово є ключовим у формулюванні теореми?

•     Змоделюйте ситуацію, що відповідає умові теореми без цього ключового слова. Які варіанти взаємного розміщення прямої та площини можливі при цьому?

2) Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.

При доведенні теореми звертаю увагу учнів на те, що допоміжна пряма , яка проходить у площині через точку є довільною.

Задаю питання:

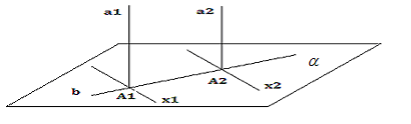
•     Як розміщена допоміжна пряма 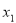відносно прямої 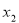? В якій площині вона знаходиться?
•     Чому ?
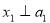•     Чому ?
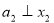•     Чому ?

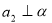Проблемне питання: Чи буде доведення цієї теореми правильним, якщо в ході доведення спочатку провести довільну пряму , а потім ||?

Даний метод являє собою діалог учителя з колективом учнів. Основна його ознака – наявність не просто „питання – відповідь”, а евристичної бесіди.

Учитель сам ставить проблему і розв’язує її за допомогою учнів, так як вони активно приймають участь у постановці проблеми, висувають пропозиції і доведені гіпотези, ми маємо справу з творчою діяльністю особистостей, завжди здатних до пошуку.