Проект на тему «Основи комбінаторики теорія ймовірності та статистики»

  ПРОЕКТ

 На тему:

 

 

«Основи комбінаторики теорія ймовірності та статистики»

 

 

 

 

 

 

                                                                                                   Підготував:

 

                                                                                                   Кременчук Ярослав

 

                                                                             9 клас

 

                                        План до теми:

 

 

 

 

 

1. Математичне моделювання
2. Відсоткові розрахунки
3. Форма складних відсотків
4. Випадкова подія. Ймовірність випадкової події
5. Статистичні дані. Способи подання даних
6. Частота. Середнє значення
7. Приклади розв'язування типових вправ

 

             Математичне моделювання

 

 

 

 

 

Математична модель — опис якого-небудь реального об'єкта або процесу мовою математичних понять, відно­шень, рівнянь тощо.

Схема розв'язування задачі математичним моделюванням

1. Сформулювати задачу мовою математики (побудувати мате­матичну модель задачі).

2. Розв'язати одержану математичну задачу.

3. Записати математичний розв'язок мовою, якою була сфор­мульована дана задача.

Якщо задача, що розв'язується математичним моделюван­ням, записана із використанням нематематичних понять, то таку задачу називають прикладною.

.

 

               Відсоткові розрахунки

 

 

 

Відсо́ток (лат. «pro centum» — сота частка, на сто). Відсотком якого-небудь числа називають соту частину цього числа.

Позначається знаком % і означає соту частку.

{\displaystyle 1\ \%=10^{-2}=0{,}01}.

Відповідно

                                               n%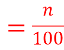

 

Знак відсотка не є скороченням одиниці вимірювання, {\displaystyle n\%\ }n% від певної величини матимуть таку ж одиницю вимірювання, як і ця величина: 5 % від певної відстані буде відстанню, 230 % від певної суми грошей буде сумою грошей, 50 % від безрозмірнісної величини буде безрозмірнісною величиною.

Коли виникає потреба порівняти дві подані у відсотках величини, їх різницю виражають у відсоткових пунктах (в.п.). Наприклад, якщо ставка за депозитом зросла з 10 % до 12 %, то кажуть, що вона зросла на 2 відсоткові пункти (в.п.). Твердження «ставка зросла на 2 %» є неправильним, оскільки 12 є більшим за 10 на 20 %, а не на 2 %.

 

              Формула складних відсотків

 

Зазвичай людина стикається з поняттям складні відсотки вперше в той момент, коли відвідує банк з метою отримати розрахунок по доходу від свого вкладу.

Складний відсоток — це збільшення інвестиційних капіталів, яке відбувається за рахунок отримання прибутку, який в свою чергу реінвестується. Це означає, що ваш дохід приймає участь в отриманні нових доходів за наступний розрахунковий період. Таким чином, за рахунок того, що ви свій капітал постійно реінвестуєте, ви отримуєте прибуток швидше і в більшому розмірі, ніж від простого депозитного вкладу. Банки визначають термін «складний відсоток», як капіталізацію. У народі «складний відсоток» ще називають як відсотки на відсотки.

 

Початковий капітал А0, внесений до банку під p %  річних, через n років стане нарощеним капіталом Аn, розмір якого обчислюється за формулою:

 

Нарахування складних відсотків (річних і не тільки) припускає, що всі отримані від вкладу проценти, ви не будете забирати і виводити з банку, а станете їх додавати до суми основного вкладу. Таке розумне рішення призводить до того, що нарахування відсотків на наступний період інвестування вже відбувається не на розмір основної суми, а на ту кількість коштів, яка вийшла у вас в результаті добавки відсотків за цим вкладом.

Таким чином, утворюється циклічність капіталізації: нарахування відсотків відбувається на відсотки і отримана сума додається до основної.

Звичайна процентна ставка найчастіше трохи вище, ніж при складному відсотку, але якщо порівнювати кінцевий результат, то при нарахуванні саме складного відсотка, ваш капітал ефективніше збільшується.

Випадкова подія. Ймовірність випадкової події

 

Випадкова подія — подія, яка при заданих умовах може як відбутись, так і не відбутись, при чому існує визначена ймовірність p (0 ≤ p ≤ 1) того, що вона відбудеться при заданих умовах. Випадкова подія є підмножиною простору елементарних подій.

Ймовірність — це числова характеристика можливості настання випадкової події за певної умови, яка може бути відтворена необмежену кількість разів. Імовірністю випадкової події називається відношення кількості елементарних подій, які сприяють цій події, до кількості всіх однаково можливих несумісних подій, які утворюють повну групу подій під час певного ви­пробування. Імовірність події знаходять за формулою P дорівнює відношенню чисел m і n, де n— загальна кількість однаково можливих і несумісних подій, які утворюють повну групу; m — число елементарних подій, які сприяють події. 

 

Якщо подія обов'язково відбудеться при багаторазовому випробуванні, то вона називається вірогідною.

Якщо подія не відбудеться при багаторазовому випробуванні, то вона називається неможливою.

Р(А) =  — формула обчислення ймовірності, де Р(А) — ймовірність події А; m — кількість сприятливих випробувань (коли подія А настала); n — кількість усіх випробувань.

Властивості ймовірності будь-якої події

1. 0 ≤ Р(А) ≤ 1. 2. Якщо А — вірогідна подія, то Р(А) = 1. 3. Якщо А — неможлива подія, то Р(А) = 0. 4. Якщо А — випадкова подія, то 0 < Р(А) < 1.

 

                                                        

Статистичні дані. Способи подання даних

Математична статистика — розділ математики, який присвячений методам збору й обробки математичних даних та їх використанню для наукових і практичних спостережень.

Основні поняття математичної статистики

1. Статистичні дані — сукупність чисел, які дають кількісну характеристику ознак певних об'єктів та явищ, що нас цікавлять. 2. Відібрану для спостереження сукупність об'єктів називають вибірковою сукупністю або вибіркою. 3. Кількість об'єктів сукупності називають об'ємом сукупності. 4. Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіантами; послідовність варіант називають варіаційним рядом. 5. Частоти — числа, які показують, скільки разів повторювалось кожне значення ознаки сукупності. 6. Відношення частоти до об'єму вибірки називають відносною частотою.

Для обробки статистичних даних виконують їх зведення, тобто упорядковують, узагальнюють статистичні дані.

Способи зведення статистичних даних:

1) складання статистичного ряду;

2) складання статистичної таблиці розподілу вибірки;

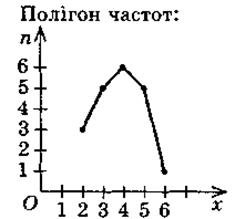
3) складання полігона частот;

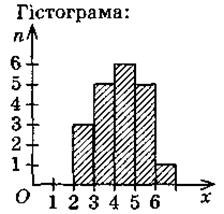
4) складання гістограм.

                                                                                                                              

               Частота. Середнє значення

Частота́ (англ. frequency) — фізична величина, що дорівнює кількості однакових подій за одиницю часу^[1]. Вона є характеристикою будь-яких процесів, які регулярно повторюються (кількість подій за одиницю часу) або величиною, що виражає: кількість рухів, коливань, повторень за одиницю часу тощо.

До регулярних процесів належать періодичні, такі як коливання або обертання, і випадкові процеси, що відбуваються неперіодично, але з певною закономірністю. Частота — одна з основних характеристик багатьох процесів у природі та техніці. Частота звукової хвилі сприймається людським вухом як тон, частота електромагнітної хвилі світлового діапазону сприймається людським оком як колір.

 

Одиницею вимірювання частоти в Міжнародній системі одиниць (SI) є герц (українське позначення: Гц; міжнародне: Hz)^[2], що отримала назву на честь німецького фізика Генріха Герца.

Для характеристики різноманітних процесів на практиці зручно використовувати також інші одиниці, наприклад, частота обертання в механічних пристроях та двигунах часто позначається в кількості обертів за хвилину (позначення: об/хв, 1/хв, хв⁻¹ або міжнародний варіант rpm від англ. revolutions per minute) чи обертів за секунду (позначення: об/с, с⁻¹ або міжнародне r/s)

 

 

   Приклади розв'язування типових вправ

 

1. Задача на тему «Математичне моделювання»:

 

Розв’язати пряму задачу симплексним методом і потім двоїсту по відношенню до неї задачу.

Побудувати математичну модель задачі.

Меблева фабрика виготовляє столи, стільці, тумби і книжкові шафи використовуючи дошки двох видів, причому фабрика має 500 м2дошок першого виду і 1000 м2дошок другого виду. Задані також трудові ресурси в кількості 800 людино-годин. У таблиці наведені нормативи витрат кожного виду ресурсів на виготовлення одного виду і прибуток від реалізації одиниці виробу.

Ресурси	Витрати на один виріб				Запас сировини, м2
	Столи	Стільці	Тумби	Книжкові шафи
Дошки І виду, м2	5	1	9	12	500
Дошки ІІ виду, м2	2	3	4	1	1000
Трудові ресурси, люд.год.	3	2	5	10	800
Прибуток від реалізації одного виробу, грн.од.	12	5	15	10

Визначити асортимент, що максимізує прибуток.

Розв’язок

Складаємо математичну модель задачі. Позначимо через х1кількість виробів 1-ї моделі, що виготовляє фірма за деяким планом, а через х2 кількість виробів 2-ї моделі та через та через х3і х4кількість виробів 3-ї і 4-ї моделі відповідно. Тоді прибуток, отриманий фабрикою від реалізації цих виробів, складає

∫ = 12х1+5х2 + 15х3+ 10х4.

Витрати сировини на виготовлення такої кількості виробів складають відповідно

А =5х1+1х2 + 9х3+ 12х4,

В =2х1+3х2 + 4х3+ 1х4,

С =3х1+2х2 + 5х3+ 10х4,

Оскільки запаси сировини обмежені, то повинні виконуватись нерівності:

5х1+1х2 + 9х3+ 12х4≤ 500

2х1+3х2 + 4х3+ 1х4≤ 1000

3х1+2х2 + 5х3+ 10х4≤ 800

Оскільки, кількість виробів є величина невід'ємна, то додатково повинні виконуватись ще нерівності: х1> 0, х2> 0, х3> 0, х4> 0.

Таким чином, приходимо до математичної моделі (задачі лінійного програмування):

Знайти х1 , х2, х3 та х4 такі, що функція ∫ = 12х1+5х2 + 15х3+ 10х4 досягає максимуму при системі обмежень:

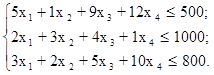
Розв'язуємо задачу лінійного програмування симплексним методом. Введемо балансні змінні х5 ≥ 0, х6≥ 0, х7≥ 0. Їх величина поки що невідома, але така, що перетворює відповідну нерівність у точну рівність. Після цього, задача лінійного програмування набуде вигляду: ∫ = 12х1+5х2 + 15х3+ 10х4 → max при обмеженнях

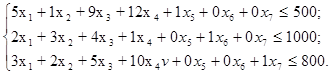
де х1,...,х7>0

Оскільки завдання вирішується на максимум, то ведучий стовпець вибирають по максимальному негативному кількістю та індексного рядку. Всі перетворення проводять до тих пір, поки не вийдуть в індексному рядку позитивні елементи.

Переходимо до основного алгоритму симплекс-методу.

План	Базис	В	x1	x2	x3	x4	x5	x6	x7	min
1	x5	500	5	1	9	12	1	0	0	55.56
x6	1000	2	3	4	1	0	1	0	250
x7	800	3	2	5	10	0	0	1	160
Індексний рядок	F(X1)	0	-12	-5	-15	-10	0	0	0	0

Оскільки, в індексному рядку знаходяться негативні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х3, оскільки значення коефіцієнта за модулем найбільше.

План	Базис	В	x1	x2	x3	x4	x5	x6	x7	min
2	x3	55.56	0.56	0.11	1	1.33	0.11	0	0	100
x6	777.78	-0.22	2.56	0	-4.33	-0.44	1	0	0
x7	522.22	0.22	1.44	0	3.33	-0.56	0	1	2350
Індексний рядок	F(X2)	833.33	-3.67	-3.33	0	10	1.67	0	0	0

Даний план, також не оптимальний, тому будуємо знову нову симплексну таблицю. У якості ведучого виберемо елемент у стовбці х1.

План	Базис	В	x1	x2	x3	x4	x5	x6	x7	min
3	x1	100	1	0.2	1.8	2.4	0.2	0	0	500
x6	800	0	2.6	0.4	-3.8	-0.4	1	0	307.69
x7	500	0	1.4	-0.4	2.8	-0.6	0	1	357.14
Індексний рядок	F(X3)	1200	0	-2.6	6.6	18.8	2.4	0	0	0

Даний план, знову не оптимальний, тому будуємо знову нову симплексну таблицю. У якості ведучого виберемо елемент у стовбці х2.

План	Базис	В	x1	x2	x3	x4	x5	x6	x7	min
4	x1	38.46	1	0	1.77	2.69	0.23	-0.08	0	500
x2	307.69	0	1	0.15	-1.46	-0.15	0.38	0	307.69
x7	69.23	0	0	-0.62	4.85	-0.38	-0.54	1	357.14
Індексний рядок	F(X4)	2000	0	0	7	15	2	1	0	0

Оскільки всі оцінки >0, то знайдено оптимальний план, що забезпечує максимальний прибуток: х1=38.46, х2=307.69, х3=0, х4=0, х5=0, х6=0, х7=69.23. Прибуток, при випуску продукції за цим планом, становить 2000 грн.

Відповідь: 2000 грн.

2. Задача на тему «Відсоткові розрахунки»

 

Знайдіть:

1) 50% від числа 48;   

2) 20% від числа 60;   

3) 150% від числа 20.

1) 50% від числа 48 = 24;

2) 20% від числа 60 = 12;

3) 150% від числа 20 = 30.

Відповідь: 1) 24; 2) 12; 3) 30.

 

3. Задача на тему «Формула складних відсотків»

Вкладник поклав до банку 10000 грн. під 16% річних. Скільки грошей буде на рахунку вкладника через 2 роки? Скільки відсоткових грошей отримає вкладник через 2 роки?

Розв’язання. А₀ = 10000 ; р = 16%; n = 2 . Маємо

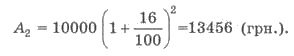
Вкладник отримає таку кількість відсоткових грошей

А₂ – А₀ = 13456 -10000 = 3456 (грн.).

За формулою складних відсотків можна розв’язувати також задачі, не пов’язані з нарощенням капіталу.

 

Відповідь: 3456 грн.

 

4. Задача на тему « Випадкова подія. Ймовірність випадкової події»

На картках записані натуральні числа: від 1 до 15. Навмання вибирають дві з них. Яка ймовірність того, що сума чисел, записаних на цих картках дорівнює 10?

Розв’язання.  Кількість всіх можливих випадків — це кількість способів, якими можна (без врахування порядку) вибрати дві картки з п’ятнадцяти. Отже, n = С²₁₅ = 105. Нас влаштовують такі набори (1;9), (2;8), (3;7), (4;6). Отже, 

 

 

Відповідь:

 

 Задача на тему «Випадкова подія. Ймовірність випадкової події»

Економіст, аналізуючи тарифні розряди працівників одного із цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди: 4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 — вибірка, що піддається обробці.

Статистичний ряд цієї вибірки: 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6; Статистична таблиця розподілу вибірки:
	Тарифний розряд х1	2	3	4	5	6
	Кількість робітників п	3	5	6	5	1