Проєктна робота "Гармонія між математикою та літературою"

Про матеріал

Використання дослідницьких матеріалів поглиблює інтерес до вивчення математики, вказує на її прикладне спрямування. Матеріали даної роботи можуть бути використані на інтегрованих уроках з математики та літератури, на заняттях гуртка. В роботі практично підтверджений зв’язок між математикою та літературою.

Перегляд файлу

Мала академія наук учнівської молоді

Відділення : математика

Секція: прикладна математика

ГАРМОНІЯ МІЖ МАТЕМАТИКОЮ ТА ЛІТЕРАТУРОЮ

АНОТАЦІЯ

Гармонія між математикою та літературою

Життя людини і суспільства постійно вимагає складних рішень, що виходять за рамки будь-якої професії, будь-якого спеціалізованого способу думки. Математика, як би не здавалось це парадоксальним, не така вже й далека від літератури. Відомо, що багато видатних математиків захоплювались літературою, а чимало письменників, поетів з задоволенням займались математикою.

У дослідницькій роботі показано, що взаємозв’язок математичного та літературного пізнання світу тісний.

Проведено пошук математичних задач в літературних творах, в народних приказках та прислів’ях, розв’язано деякі з них.

Для гуманітаріїв показано, що вивчення математики, яку вони переважно розглядають як науку «суху» та нецікаву, перетворюється на захоплюючий пошук математичних закономірностей розв’язування життєвих задач.

Наукова новизна роботи: практично змодельовано залежність рівня води від кількості та об’єму занурюваних у неї предметів.

Значення проробленої роботи полягає в тому, що матеріали даної роботи можуть бути використані на інтегрованих уроках з математики та літератури, на заняттях гуртка. Використання дослідницьких матеріалів поглиблює інтерес до вивчення математики, вказує на її прикладне спрямування.

Висновок: В ході виконання проєкту було знайдено підтвердження того, що зв’язок між математикою та літературою дуже тісний, підтверджено припущення про те, що багато поетів і письменників все-таки є математиками в душі і багатьом математикам властиві поетичні таланти.

Для учнів, які полюбляють гуманітарні науки і для тих, хто в захваті від точних наук доведено, що і математика, і література науки дуже цікаві і тісно пов’язані між собою.

Ключові слова: математика, задача, розв’язання, література, поезія, взаємозв'язок.

ЗМІСТ

ВСТУП……………………………………………………………………………….5

РОЗДІЛ 1 МІСЦЕ МАТЕМАТИКИ І ЛІТЕРАТУРИ В ЖИТТІ СУЧАСНОГО СУСПІЛЬСТВА……………………………………………………………………..6

РОЗДІЛ 2 ВЗАЄМОЗВ’ЯЗОК МАТЕМАТИКИ ТА ЛІТЕРАТУРИ……………..7

2.1. Піфагор – філософ, математик…………………………………………...7

2.1.1 Задача Піфагора……………………………………………………..7

2.1.2 Золоті вірші Піфагора……………………………………………….9

2.2 Задача «Чи багато людині землі треба?……………………………….....10

2.3. Задача про здогадливу ворону…………………………………………..12

2.3.1 Експериментальна частина………………………………………...13

2.3.2 Обчислювальна частина……………………………………………14

2.3.3 Висновки до задачі………………………………………………….16

РОЗДІЛ 3 МАТЕМАТИКА В НАРОДНІЙ ТВОРЧОСТІ………………………..17

3.1 Математика в прислів’ях та приказках…………………………………...17

3.2. Поезії та пісні мовою цифр……………………………………………….18

ВИСНОВКИ………………………………………………………………………….20

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………………………………...........22

ДОДАТКИ……………………………………………………………………………23

ВСТУП

Математика тренує розум для математичних істин, а письменство – для моральних.

Ж. Жубер, французький письменник

«Нематематичні» захоплення видатних математиків та «математичні» захоплення визначних письменників і поетів привертають увагу людей до загальнолюдських цінностей і культури, показують різносторонній розвиток творців науки. Гармонійна людина повинна знати добре і математику, і літературу.

Актуальність теми пов`язана з тим, щоб довести, що література існує не тільки для літераторів, як і математика не тільки для математиків.

Мета роботи: показати тісний зв'язок між математикою та літературою; розкрити та охарактеризувати приклади використання математичних категорій у контексті змісту літературних творів різних жанрів; сформувати систему знань прикладного використання математичних інструментів та моделей в літературі та народній творчості.

Предмет дослідження: математичні задачі в літературних творах, народні прислів’я з математичними величинами.

Об’єкт дослідження: фрагменти творів світової та української літератури, прислів’я та приказки.

Завдання дослідження:

1) знайти математичні задачі в літературі, по можливості розв`язати та пояснити їх;

2) підібрати математичні задачі в художній літературі для дослідження;

3) розширення кругозору;

4) розв’язання поставлених завдань та оцінка отриманих результатів.

Методи дослідження: аналіз науково-популярної та художньої літератури, аналіз та рішення, порівняння результатів із реальною дійсністю.

РОЗДІЛ 1

МІСЦЕ МАТЕМАТИКИ І ЛІТЕРАТУРИ В ЖИТТІ СУЧАСНОГО СУСПІЛЬСТВА

Математика і література займають значне місце в житті сучасного суспільства, а це означає, викликають до себе величезний інтерес.

Що може об'єднувати ці далекі одна від одної області знань? Літературу, з її інтересом до духовного світу людини, і математику, яка віддає перевагу строгому науковому підходу. Літературу ми звикли відносити до гуманітарних наук, а математика вимагає точності і конкретизації фактів.

Здавалося б, немає нічого спільного ... Але математика, так само як і поезія, живопис, театр і мистецтво прагне до пізнання і краси. Що люблять, то знаходять скрізь, і було б дивно не зустрітися з математикою в художній літературі.

Розглядаючи взаємозв’язок математики та літератури можна виділити три напрямки. Перший висвітлюється з точки зору впливу математики на літературу. У даному аспекті математика є основою для вибору тем, сюжетів; математика може бути складовою художнього твору. Автор, знаючи математичні закони, закономірності створює достовірний з наукової точки зору високохудожній твір. Другий напрямок характеризується впливом літератури на математику, де література є постачальником інформації для математики. Третій напрямок полягає у тісному діалозі математики та літератури в творчості письменників.

Математична наука є частиною інтелектуального багатства людства, без якої не може відбутися ні письменник, ні поет. Математика постає для літераторів джерелом інформації, живить знаннями, постачає темами, сюжетами.

Грамотне використання математичних фактів робить художній твір достовірним і реальним.

РОЗДІЛ 2

ВЗАЄМОЗВ’ЯЗОК МАТЕМАТИКИ ТА ЛІТЕРАТУРИ

2.1. Піфагор – філософ, математик

З давніх-давен про славу математики, про її красу, логічність, стислість, бездоганну послідовність, дивовижні її результати писали не тільки великі математики, а й філософи, письменники, політики.

Піфагор Самоський – великий грецький вчений, людина–символ, філософ та пророк. Він організував школу, яку назвали піфагорійською.

Діяльність школи була оточена таємницею. Піфагор вчив, що "число є сутністю всіх речей". Він займався астрономією, геометрією, гармонією (теорією музики) та арифметикою (теорією чисел).

2.1.1 Задача Піфагора

Тиран острова Самос Полікрат одного разу запитав Піфагора, скільки у того учнів.

"Охоче скажу тобі, о Полікрате, - відповідав Піфагор. - половина моїх учнів вивчає прекрасну математику, чверть досліджує таємниці вічної природи, сьома частина мовчки вправляє силу духу, зберігаючи в серці вчення. Додай до них трьох юнаків, з яких Теон перевершує інших здібностями. Стільки учнів веду я до народження вічної істини". Скільки учнів було у Піфагора?

Розв’язання

Нехай x - загальна кількість всіх учнів;

– любителі математики;

- любителі природи;

- мовчуни;

3 – юнаки.

Маємо рівняння:

Розв’яжемо його:

14x + 7x + 4x + 84 = 28x;

28x – 25x = 84;

3x = 84;

х = 28.

Отже, у школі Піфагора налічувалось 28 учнів. Із них – 14 любили математику; 7 – любителі природи; 4 – мовчали, і ще було троє юнаків.

А ось так виглядає зміст цієї задачі в перекладі видатного українського письменника, прозаїка, поета І. Я. Франка, який не тільки перекладав віршовані задачі старогрецьких математиків, а й шукав способи їх розв’язання.

Учні Піфагора

«Піфагоре благородний,

Геліконських муз потомку,

На моє скажи питання,

Скільки учнів справді гідних

Маєш ти у своїм домі,

Що немов борці на площі,

Раді премії добиться?»

«Радо скажу, Полікрате.

Бачиш, учнів половина

Математику зглибляє,

А натомість четвертина

На безсмертную природу

Свої досліди звертає.

Сьома часть ніщо не робить,

Лиш заховує мовчання,

Лиш моє у душах своїх,

Знай, ховаючи мовчання.

Ще додай до них три жінки,

Що встають не дуже рано,

– Серед них найвизначніша

Моя любая Теано.

Ось і всі, яких по змозі

Я до мудрості доводжу,

– Може, муз їм пієрійських

Позискаю ласку божу».

Скільки ж учнів у Піфагора?

2.1.2 Золоті вірші Піфагора

Для початківців школи Піфагор-математик написав «Золоті вірші». Літературний переклад «Золотих віршів Піфагора»:

Золоті вірші Піфагора

Матір і батька поважай, також — і ближніх твоїх.

Пам’ятай про закон причин і наслідків у долі твоїй.

І будучи на самоті, і на людях — бійся здійснити вчинок негідний! Честь свою бережи!

Будь завжди справедливий і у словах, і у вчинках своїх, дотримуючись непохитно і велінь, і розуму, і закону.

Багато можливостей вибору є у людей. Чимало можливостей тих зовсім дурних, а багато і добрих. Тому спершу треба в них пильно вдивитись, аби вибрати гідний шлях для самого себе.

Якщо ж серед люду облуда горою над правдою стане — то мудрий відійде і ждатиме часу, коли істина знов воцарює.

Слухай поради людей, сам розмірковуй невпинно! Адже лиш дурень вдається до дій, не осмисливши все попередньо!

Роби лише те, що потім тобі ж не завдасть горя-болю і не буде причиною для каяття і докорів сумління!

За тобі невідому ще справу не берися одразу, але вивчи її, їй навчися — лиш тоді ти до успіху будеш за крок!

У житті своєму дотримуйся — скільки зможеш — порядку.

Бійся бути скупим!

Роби лише те, що тебе ні тепер, ані потім не згубить!

Тож хай не зімкне сон твої обтяжені повіки, допоки ти тричі не згадаєш вчинки свої для прожитого. Мов безпристрасний суддя ти їх обміркуй, запитуючи себе: “Що доброго я зробив? Що не виконав з того, що конче зробити мав?”

Знатимеш ти ще і те, що люди нещастя свої всі самі на себе накликають — своєю провиною, бо не відають! А ще вільно вони вибирають долі свої!

Замість того, щоб сварку шукати, де треба й не треба, — люди мають її уникати, поступаючись — без суперечки...

І утримуйся від харчування плоттю: це непритаманне природі твоїй і заважатиме при очищенні твоєму!

Тож, якщо хочеш позбутися ти пут земного, то керуйся цим розумінням, даним тобі! Нехай воно — править долею твоєю!

2.2 Задача «Чи багато людині землі треба?

«Є люди, обдаровані в значній мірі моральним і художнім почуттям, і є люди, майже позбавлені його. Перші ніби зразу беруть інтеграл. А другі виконують складні обчислення, які не призводять до кінцевих висновків. Нібито перші виконали всі обчислення раніше, а тепер користуються результатами» - писав один із найвідоміших російських письменників і мислителів, просвітник, публіцист, релігійний мислитель, який брав участь в обороні Севастополя, Лев Миколайович Толстой.

У своїх літературних творах Л. Толстой пропонував багато цікавих задач. Його творчість глибоко пронизана математичними ідеями. Глибину морального змісту видно в оповіданні Л. Толстого «Чи багато людині землі треба». Ось уривок з нього.

«Роками мріяв селянин Пахом про власну землю. Довго гроші збирав, відмовляючи собі в усьому! І ось, нарешті, зібрав заповітну суму…

– А ціна ж землі яка буде? – говорить Пахом.

– Ціна у нас одна: 1000 крб. За день, – відповів старшина.

Не зрозумів Пахом.

– Яка ж це міра – день? Скільки в ній десятин буде?

– Ми цього, – каже, – не вміємо рахувати. А ми за день продаємо: скільки обійдеш за день, те і твоє, а ціна 1000 крб.

Здивувався Пахом.

– Так це ж, – каже, – за день землі багато буде.

Засміявся старшина.

– Вся твоя, тільки одна умова, якщо назад не повернешся вдень до того ж місця, з якого вийдеш, пропали твої гроші.

Тільки зійшло сонце, вирушив Пахом від мітки. Пройшов верст 10, вирив ямку й звернув круто вліво. Пройшов по цій стороні ще більше, загнув другий кут. Третьою стороною пройшов усього 2 версти, глянув на сонце, а воно вже низенько, а до мітки ще верст 15 буде. Вирив ямку і став напрямки поспішати. Іде, іде, важко йому стало, відпочити хочеться, але не можна: сонце вже зовсім низько. Прискорив ходу, а воно ще далеко. Побіг риссю. Біжить, сорочка до тіла липне, в роті пересохло, серце молотком б’є. Глянув, сонце вже заходити починає. Наддав з останніх сил. Прибіг до місця, впав, руками до мітки дістав.
- Ну й молодець! Багато землі придбав!- вигукнув старшина.

Підбіг слуга, щоб допомогти Пахому підвестись, але той уже мертвий лежав...»

Скільки ж землі відміряв Пахом за день невпинного ходу?

Я. Перельман вважав, що за даними, наведеними в оповіданні, можна накреслити план ділянки, яку оббіг Пахом. Він біг по сторонах чотирикутника. Про першу сторону в оповіданні сказано: «Верст п’ять пройшов… Пройду ще верст з п’яток; тоді буду вліво завертати». Отже, довжина першої сторони чотирикутника близько десяти верст, АВ=10. Про довжину другої сторони ВС, перпендикулярної до першої, даних немає. Довжина третьої сторони, перпендикулярної до другої, відома з оповідання: «По третій стороні всього версти дві пройшов», CD=2. Відома і четверта сторона: «До місця все тих самих верст 15», тобто AD=15.

Розв’язання

Потрібно знайти площу трапеції ABCD з основами АВ і CD та висотою DK. КВ = CD =2. Тоді АК = АВ – КВ = 10 – 2 = 8. Висота трапеції DK невідома, тому знаходжу її з трикутника АDK, застосувавши теорему Піфагора.

АD²= АK²+ DK². Звідси, DK²= АD² - АK², DK²= 15² – 8² =161, 16113. ВС= DK=13

S_ABCD=

S_ABCD=.

Відстань, яку пройшов протягом дня Пахом є периметром трапеції ABCD.

Р_АВСD= АВ+ВС+CD+ АD;

Р_АВСD=10+13+2+15=40(верст)

Висновок

Якби селянин Пахом був обізнаний з математикою, то він, обійшовши ділянку периметром 40 верст, але у вигляді квадрата зі стороною 10 верст, мав би більшу площу:

S_{квадрата}= 10·10 = 100(кв. верст)

2.3. Задача про здогадливу ворону

Нещодавно я прочитала кумедне оповідання про здогадливу ворону, засновану на старовинній легенді. Ця старовинна легенда оповідає про ворону, що страждала від спраги і знайшла глечик з водою.

«Дві ворони ходили шукати води, бо їм дуже хотілося пити, але не знайшли ніде. Нарешті знайшли десь на кошарі в збанку, та не могли дістати, бо води було мало. Одна ворона полетіла далі. Друга ворона почала до збанка метати камінчики, щоби вода наверха вийшла, і напилась. Недарма люди кажуть: де не візьмеш силою, бери умом.»

Води в глечику було мало, дзьобом її не дістати, але ворона ніби зрозуміла, як допомогти горю: вона стала кидати в глечик камінчики. В результаті цього прийому рівень води піднявся до країв глека, і ворона могла напитися.

2.3.1 Експериментальна частина

Для досліду я взяла глечик, мірний циліндр, велике каміння та камінчики гравію (Додаток А).

Далі розглянула три випадки: чи вдалося б напитися вороні, якби води в глеку було налито:

а) менше половини (Додаток Б);

б) до половини (Додаток В) ;

в) більше половини (Додаток Г)?

Провела два експерименти: з великим камінням та дрібним.

Розбір завдання переконує, що спосіб, застосований вороною, призводить до мети не при кожному початковому рівні води в глеку. Для спрощення приймемо, що глечик має форму куба, а камінці є кульками однакової величини. Легко збагнути, що вода піднімається над рівнем каменів лише в тому випадку, якщо початковий запас води має більший об’єм, ніж усі проміжки між камінчиками: тоді вода заповнить проміжки і виступить поверх камінчиків. Можна визначити об’єм проміжків, заповнених водою, експериментально.

2.3.2 Обчислювальна частина

Я наливала в глечик воду, попередньо вимірявши її об’єм в мірному циліндрі, розглядаючи всі три випадки.

Експеримент 1. Велике каміння (великі кульки).

Радіус кульки R=2 см, тоді об’єм її

V_кулі==см³)

а об’єм описаного біля нього кубика

V_куба=8R³=8(см³)

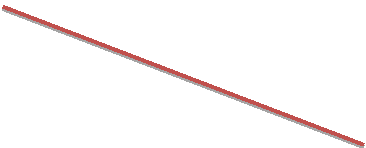
Різниця їх об’ємів: V_куба -V_кулі = 64-33 = 31(см³)

є об’єм незаповненої частини кубика. А відношення . Це означає, що незаповнена частина кожного кубика становить 0,48 його об’єму. В глечик помістили N=11 великих камінців, тоді об’єм порожнечі V_{порожнечі}= N (V_куба -V_кулі)= 341(см³). Отже,

- якщо об’єм води дорівнює 305 см³, то об’єм порожнечі більший і тому вода не підіймається вище камінців (Додаток Д);

- якщо об’єм води дорівнює 403 см³, то вода підіймається вище камінців на 1 см (Додаток Е);

- якщо об’єм води дорівнює 804 см³, то вода підіймається вище камінців на 3 см (Додаток Ж).

Експеримент 2. Дрібні камінці.

Радіус кульки R=0,5 см, тоді об’єм її

V_кулі==см³)

а обсяг описаного біля нього кубика

V_куба=8R³=8(см³)

Різниця їх об’ємів: V_куба -V_кулі = 1-0,52 = 0,48(см³)

є об’єм незаповненої частини кубика. А відношення В глечик помістили N=640 маленьких камінців, тоді об’єм порожнечі V_{порожнечі}= N (V_куба -V_кулі)= 307(см³). Отже,

- якщо об’єм води дорівнює 305 см³, то об’єм порожнечі приблизно рівний кількості води і тому вода знаходиться на рівні камінців (Додаток И);

- якщо об’єм води дорівнює 403 см³, то вода підіймається вище камінців на 2 см (Додаток К);

- якщо об’єм води дорівнює 804 см³, то вода підіймається вище камінців на 5 см (Додаток Л).

Результати вимірювань занесені до таблиць

Початковий рівень води	Об’єм води до наповнення глечика камінням, см³	Рівень води після наповнення глечика камінням
Початковий рівень води	Об’єм води до наповнення глечика камінням, см³	Велике каміння	Дрібне каміння
Нижче половини	305	Нижче каміння	Вище каміння
Половина	403	Вище на 1 см	Вище на 2 см
Вище половини	804	Вище на 3 см	Вище на 5 см

Таблиця обчислень

	R=2 см	R=0,5 см
V_кулі=(см³)	33	0,52
V_куба=8R³(см³)	64	1
V_куба -V_кулі(см³)	31	0,48
	0,48	0,48
N(кількість кульок)	11	640
V_{порожнечі}= N (V_куба -V_кулі)(см³)	341	307

2.3.3 Висновки до задачі:

- коли б вода наповнювала глек нижче половини висоти глека або займала б половину висоти глека - вороні не вдалося б напитися;

- коли б вода наповнювала глек вище половини висоти глека - ворона б напилася.

Результати експерименту підтверджують теоретичне розв'язання задачі.

Була б ворона сильнішою - настільки, щоб утрясти камінчики в глеку і добитися їх щільного укладання( як у експерименті 2) - їй вдалося б підняти воду вище за початковий рівень. Але їй це не під силу зробити.

Я перевірила, якщо брати дуже дрібне каміння, то вода піднімається вище. У реальних умовах пухке розташування камінчиків допустиме. До того ж глечики зазвичай роздуті в середній частині; це має так само зменшити висоту підйому води, і підкріплює правильність судження, що від форми судини і висоти води в глечику залежить вирішення проблеми: чи змогла ворона напитися води?

РОЗДІЛ 3 МАТЕМАТИКА В НАРОДНІЙ ТВОРЧОСТІ

3.1 Математика в прислів’ях та приказках

Дуже часто зустрічаються математичні поняття в народних прислів’ях та приказках.

Про дуже розумну людину кажуть «премудра голова», «мудрагель». У російській мові існує навіть вираз «семь пядей по лбу». Чи існує людина, що має чоло розміром «сім п’ядей»?

Відомо, що 1 п’ядь = 18 см, 7 п’ядей = 187=126 см, неважко зрозуміти, що відповідь буде негативною.

А який зріст людини, яку називають « коломенською верстою»?

Під час царювання Олексія Михайловича Романова вздовж дороги від Москви до Коломенського були розставлені на відстані 500 сажнів один від одного верстові стовпи з орлами висотою у 2 сажні. Враження від них у людей було настільки велике, що залишилося в народній мові.

Як відомо, 1 сажень = 2,16 м, 2 сажні = 2,162=4,32 м. Отже, зріст такої людини понад 4 м, чого в житті не буває.

Визначивши зріст людини, про яку говорять «від горшка два вершки, а вже вказує» ( висоту горшка вважати 25 см), дістали ось що:

оскільки 1 вершок = 4,5 см, 2 вершки = 4,5 см2 = 9 см, то зріст людини 25 см + 9 см = 34 см.

Так говорили про молоду людину, що не мала життєвого досвіду, але самовпевнено про щось розмірковувала та повчала інших.

А як глибоко бачить той, про кого говорять «на три аршини, в землю бачить»?

1 аршин = 72 см, 3 аршини = 72 см3 = 216 см = 2,16 м.

Так кажуть про далекоглядну, прозорливу, уважну людину, від якої нічого неможливо приховати.

3.2. Поезії та пісні мовою цифр

В літературі дуже часто зустрічається категорія числа, що є фундаментальним поняттям математики. Воно зустрічається в назвах творів: «Три мушкетери» О. Дюма; «Дванадцять місяців» - казка; «Тисяча і одна ніч» - збірка арабських казок.

Також відомі поезії можна записати за допомогою чисел.

Тарас Шевченко «Садок вишневий…»:

„ Садок вишневий коло хати,

Хрущі над вишнями гудуть,

Плугатарі з плугами йдуть,

Співають ідучи дівчата,

А матері вечерять ждуть. ”

13 9 48

15 8 43

512 38

16 30 23

Пісня «Якби не було зими» з нашого улюбленого мультфільму «Зима в Простоквашино»:

«Як би не було зими

У містах і селах,

То не знали б зовсім ми

Днів таких веселих.

Не ліпили б дітлахи

Снігової баби

Сніг не ліг би на дахи.

Якби, якби, якби…»

3 15 42

42 15

37 08 5

20 20 20

7 14 100 0

2 00 13

37 08 5

20 20 20

Поезія надає яскравості математичним фактам і задачам, щоб ті засяяли ще яскравіше. Вона слугує гарним фоном для математики — науки точної, серйозної.
Математика і література поєднують прагнення до пізнання і творчості. Вони належать до людської цивілізації, а тому збагачують одна одну. Розум і душа, інтелект і натхнення, математика і поезія – це два крила нашої долі, які несуть нас до щастя. Вони не можуть не захоплювати своєю витонченістю і красою. Недарма відомий математик О. Казанцев сказав: „Математика - пісня розуму”

ВИСНОВКИ

Про математичні категорії в змісті літературних творів мною була висвітлена зовсім незначна частина незвіданого, безкінечного світу літератури і математики, бо фонд джерел постійно поповнюється. Закономірності математичних наук знаходять місце в текстах художніх творів як давнини, так і сучасності. Вони сприяють розумінню логіки розвитку процесу математичного та літературного пізнання світу, виявленню його сутності в математичних категоріях та в літературних художніх образах. Видатний літературознавець Ю. Лотман говорив «Можна припустити, що в культурі, в якій є математика, повинна бути і поезія і навпаки. Гіпотетичне знищення одного з цих механізмів, ймовірно, зробило б неможливим існування іншого»

За допомогою наведених прикладів мені вдалося переконати скептиків в тому, що література і математика—це два могутніх знаряддя пізнання світу, частиною якого є сама людина. Не протистояння, а поєднання математики і літератури вносить гармонію і красу у світ!

Велике математичне дарування зазвичай поєднується з проявом творчої цікавості до поезії. Фрагменти літературних творів, в яких є математичні задачі, показують тісний зв’язок математики з життям та різноманітними науками. Найкращі, найвлучніші, найдотепніші висловлювання ставали крилатими афоризмами, а цитати з оригінальних творів найвидатніших учених переходили з покоління в покоління і ставали теж, у певному розумінні, сторінками історії розвитку математики. У наукових працях, починаючи від часів Платона й Архімеда і до наших днів можна знайти немало цікавих, глибоких і оригінальних думок про математику, її розвиток тощо. Ці афоризми й висловлювання допомагають повніше розкрити різні сторони математичної науки, надихають і підбадьорюють тих, хто входить у чарівний казковий світ цифр, чисел і фігур, тих, хто присвячує цьому світові своє життя...

Отже

- в роботі досліджено тісний зв’язок між математикою та літературою;

- підтверджено припущення про те, що багато поетів і письменників є математиками в душі і багатьом математикам властиві поетичні таланти;

- розширено уявлення про широкий спектр застосування математики;

- отримані результати можуть бути використані вчителями на уроках математики та літератури.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Перельман Я. И. Занимательная геометрия. / Я. И. Перельман. – М.: АСТ, 2006. – 480 с.

2. Конфорович А. Г. Визначні математичні задачі/А. Г. Конфорович. – К.: Рад. школа, 1981 – 189с.

3. Толстой Л. М. «Три казки Льва Толстого»/ Л. М. Толстой. – 1886 р.

4. Лотман Ю. М., Петров В. М. Мистецтвометрія: методи точних наук і семіотики. М., 2019, 368с

5. Воєвода А. Математика та література: матеріали до інтегрованих уроків і заходів. Київ. 2013 р. 104 с.

6. Ляшов, Н. М. Функціонування математичних категорій у творах світової літератури / Н. М. Ляшов // Закарпатські філологічні студії. – Ужгород : Видавничий дім "Гельветика", 2019. – Т. 2. – Вип. 10

7. Джордан Еленберг «Як ніколи не помилятися», або Математика для гуманітаріїв. Наш формат, 2017. – 408с.

8. http://mmmikitchak.blogspot.com/p/blog-page_54.html Математика і література

9. Ресурс Інтернет