Проектна робота "Обчислення значення числа пі"

Проектна  робота групи учнів 9 класу

 

 

 

 

 

 

ОБЧИСЛЕННЯ ЗНАЧЕННЯ ЧИСЛА

 

	Керівник групи: Шептур Галина Євгенівна, учитель математики  Харківської гімназії №43 Харківської міської ради  Харківської області

 

 

ЗМІСТ

ВСТУП                                                                                                                       4

РОЗДІЛ  1

ОСНОВНІ  МЕТОДИ  ОБЧИСЛЕННЯ   ЗНАЧЕННЯ   ЧИСЛА  π

     1.1. Обчислення  відношення  діаметра  кола   до  його  довжини  

Архімедом                                                                                                                   7

     1.2.  Обчислення  значення  π  у  другому   тисячолітті  нашої  ери                8

РОЗДІЛ   2

ТЕОРЕТИЧНА  ЧАСТИНА  ПРОВЕДЕНОГО  ЕКПЕРИМЕНТУ

      2. 1.  Опис  та  пояснення    проведеного  експерименту                                 10

      2. 2.  Знаходження  ймовірності  р,  для  перетину  однієї  з  паралельних  прямих  та  виведення  формули  для  підрахунку  π                                             12

      2. 3.  Підрахунок  неминучої  похибки  в  отриманих  результатах 

дослідів                                                                                                                       14

РОЗДІЛ  3

 ПРАКТИЧНА  ЧАСТИНА  ПРОВЕДЕНОГО  ЕКСПЕРИМЕНТУ

       3. 1.  Дослід  І                                                                                                      16

       3. 2.  Дослід  ІІ                                                                                                    17

ВИСНОВКИ                                                                                                              18

СПИСОК   ВИКОРИСТАНИХ  ДЖЕРЕЛ                                                              21

ДОДАТКИ                                                                                                                  22

ВСТУП

          Найперші відомі записані свідчення про  відношення  довжини  кола  до  його  діаметра  датуються  близько 1900 роком до н. е.  У  той  час  це значення    ( відношення  довжини  кола  до  його  діаметра )  в  різних  країнах    відрізнялося.  Це  було  спричинено  тим,  що  дане  відношення  не може  бути точно виражене  ні цілим числом,  ні звичайним  дробом,  ні скінченним десятковим дробом,  бо  є  ірраціональним. Тому,  наприклад,  у  Єгипті  воно  дорівнювало  256/81 ≈ 3,160,  у  Вавилоні   25/8 = 3,125,  а  індійський  текст    Шатапатха-Брахмана дає значення  ,  як 339/108 ≈ 3,139 - найбільш  точне. Але  всі  вони  коливалися в межах 1 процента від істинного значення.  Ці  та  інші наближені значення π були отримані емпіричними  способами.  Наприклад,  шляхом  прямого  вимірювання довжини кола за допомогою мотузки і т. п.  .

            Але  дане  питання  про  обчислення  відношення  довжини кола до свого діаметра  і  далі   продовжувало   турбувати  кращі уми людства,  бо  вони  прагнули  знайти все  більш   точне    значення.  І,  можливо,  перше обчислення  π  на  основі  строгих  теоретичних  міркувань  було зроблено видатним  математиком  давнини  Архімедом. У своїй  роботі  «Про   вимір кола»  він довів,   що

          Наближені з нестачею і надлишком значення для π Архімед отримав, розглядаючи вписані в коло та описані навколо  нього многокутники з досить великою  кількістю сторін. Він послідовно визначав сторони вписаних і описаних шестикутників,  дванадцятикутників,  …  , дев’яностошестикутників,  виражених через  діаметр.  Створений  Архімедом  метод  обчислення  довжини  кола за  допомогою периметрів вписаних і описаних многокутників  застосовувався багатьма видатними математиками  протягом,  майже,  2000 років.  Хоча  у  деяких  країнах  Азії  зустрічається  значення   π = тобто 3,162 ... . Астроном  Ван  Фань  (229-267)  стверджував,  що  π = 3,155… .

         З  цього  можна  зробити  висновок, що тогочасні  науковці  вважали π близьким у значенні до трьох,  а  виведене Архімедом для  π  наближене значення 22/7 ≈ 3,14 виявилося цілком задовільним для практики.  На це значення посилаються Герон Олександрійський, Папп, Прокл та інші вчені.

        Починаючи з кінця XVII століття для обчислення відношення  кола  до  його  діаметра  застосовуються  більш  ефективні методи вищої математики. Леонард  Ейлер  (1707- 1783 р.) обчислив  π  з точністю до 153 десяткових знаків. Саме  після опублікування  його роботи (1736 р.) стало загально прийнятим позначення  π  (перша буква в грецькому слові «периферія» - коло),  яке зустрічається вперше в 1706 р. у англійського математика У. Джонса. У 1873 р. англієць В. Шенкс визначив π з точністю до 707 десяткових знаків,    пропрацювавши  для  цієї  мети  приблизно  15 років .

        Розвиток  обчислювальної  техніки  у  ХХ  столітті  набагато  спростив  метод  обчислення  значення  π.  Так,  з'ясувалося згодом,  що 527-й знак Шенкса виявився невірним. Помилка була виявлена ​​ Фергюссон  і  Ренч,  які в 1949 р. отримали значення  π  з 2035  знаками  за  допомогою електронних машин,  а пізніше - з 3089 знаками всього лише за 13 с. До 1963 р. було знайдено вже 100265 десяткових знаків числа  π.  Обчислення такого великого числа знаків для  π не має практичного значення, а показує лише  величезну перевагу  і  досконалість    сучасних  засобів  і  методів  обчислення  у  порівнянні зі старими  [ 3. 23 – 40 ].                                                       

              Тому  у  своїй  роботі  я  не  намагаюся з’ясувати якомога більшу кількість десяткових знаків числа  π,  а  лише   спробую  самостійно  визначити  приблизне  значення  відношення  довжини  кола  до  його  діаметра  за  допомогою  теорії  ймовірностей  та  голки.  Подібно  до  того,  як  це  робив  французький  природодослідник  Ж. Л. Л. Бюффон (1707 – 1788).  Порівнявши  результати   дослідів,  я  з’ясую  умову,  при  якій  значення  π  буде  більш  точне.  Оскільки,   досліджуючи  історію  обчислення   числа  π  за  допомогою  теорії  ймовірностей,  було  виявлено  декілька  умов  для  проведення  цього  досліду,  але при  цьому  ніде  не  зазначалося,  яка  з них приводить  до  більш  точного  результату.  У  наслідок   цього   було  вирішено   провести  два  досліди  за  різного  розташування  паралельних  прямих  відносно    руки  експериментатора і встановити,  при  якому   розташуванні  паралельних  прямих  значення  π,  в  більшості  випадків,    буде   точніше.

                 Актуальність теми даної роботи полягає в тому, що  розглядаючи  методи  знаходження  числа  π,  поглиблюються  знання  з  геометрії,  математичного аналізу,  теорії  імовірностей, що  сприяє  розширенню  математичного  кругозору.  Відшукуючи  відношення  довжини  кола  до  його  діаметра  експериментальним   шляхом  за  допомогою  методу  Бюффона   маємо  змогу  використати  набуті  знання  у школі  з  теорії  ймовірності  та  інтегрального  обчислення  на  практиці  у  надзвичайно  цікавій  та  неординарній  задачі.

     Об’єкт  дослідження  -  різні способи  обчислення  значення  числа  π.

     Предмет    дослідження – визначення  наближеного   значення  числа  π  за  допомогою  методів  теорії  ймовірностей  та  інтегрального  обчислення. 

             Мета  даної  роботи  –  визначити,   шляхом    проведення  низки  дослідів,  за  допомогою  теорії  ймовірностей  та  інтегрального  обчислення,  вплив  розташування  паралельних  прямих відносно  тіла  експериментатора  на  знаходження  числа  π  з  більшою  точністю.

  З огляду на визначену мету були поставлені наступні завдання дослідження:

• дібрати та проаналізувати літературу за темою;
• ознайомитися з історією обчислення числа π;
• детально розглянути задачу Бюффона і виокремити умови її відтворення;
• підготувати необхідні матеріали для проведення експерименту;
• з’ясувати умови проведення експерименту для знаходження більш точного значення числа π.

  Відповідно до поставлених мети і завдань було використано наступні методи: добірка необхідної літератури та її осмислення, аналіз, порівняння; систематизація теоретичних знань, експеримент, вимірювання, обробка даних.

           

                    

РОЗДІЛ  1

                 ОСНОВНІ  МЕТОДИ   ОБЧИСЛЕННЯ    ЗНАЧЕННЯ   ЧИСЛА  π

          На  мою   думку,   цікаво  буде  розглянути    методи   та   приклади  обчислення  π,  які  висвітлюють  саме  математичні  методи   розв’язання  даної  задачі.

         1.1. Обчислення відношення  довжини кола  до  його   діаметра Архімедом

         Для  обчислення  відношення  довжини  кола  до  його  діаметра                    ( числа  π )  Архімед  розглядав  правильні  многокутники  вписані  і описані  навколо  кола     (  Додаток А ). Порівнюючи  периметри  многокутників  він  визначав  верхню і нижню  границі  для  дуги  кола.   Такі  принципово нові,  на  той  час,   ідеї  та  методи  Архімед виклав у праці «Вимірювання  круга».

  У  своїх   дослідженнях   вчений  виходить  з  того,   що   довжина   кола   міститься  між  значеннями  периметрів правильних вписаних і описаних многокутників з однаковою кількістю сторін. Якщо число сторін цих многокутників необмежено подвоювати, то їх периметри наближати­муться до своєї границі – довжини кола. Архімед почав робити обчислення для правильних шестикутників і доводив їх до правильних  96-кутників.  Виконавши  таку  кількість  роботи  він  виявив, якщо  діаметр кола взяти за одиницю, то величина периметра правильного вписаного 96-кутника буде більшою від 3 , а величина периметра  правильного описаного 96-кутника буде меншою за 3  Таким  чином,  довжина  кола  знаходитися   в  межах  даних  чисел.  На  той  час   Архімеду   вдалося  знайти  π=3,14,  тобто   з точністю до 0,01. Зараз  це  значення числа  π , тобто     називають  Архімедовим.

 Запропонований  Архімедом  спосіб  дозволив  йому  теоретично  визначити з довільною точністю число  π,  як відношення довжини кола до діаметра,  задовго  до  появи  обчислювальної  техніки  [ 9 ].

       

 

 1.2.  Обчислення  значення  π  у  другому   тисячолітті  нашої  ери

           До другого тисячоліття н. е. число   було розраховане з точністю не більшою ніж 10 цифр в записі числа. Наступний великий поступ у вивченні числа   прийшов з розвитком нескінченних рядів і, відповідно, з відкриттям математичного аналізу, що дозволило розраховувати з будь-якою бажаною точністю  розглядаючи необхідну  кількість  членів  такого  ряду.

            Близько 1400 року  Мадхава  Сангамаграма  знайшов перший з таких рядів:

 

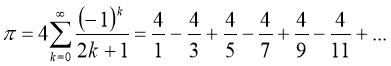
В  наш  час  цей  ряд відомий,  як ряд Мадхави - Лейбніца  або ряд  Грегорі – Лейбніца, оскільки  його знову  відкрили  Джеймс  Грегорі та  Готфрід  Лейбніц у 17-тому столітті. Проте, швидкість  наближення даного ряду занадто повільна. Щоб розрахувати багато значущих цифр на практиці, треба додати близько 4000 членів  ряду.  Хоча,  перетворивши ряд у такий вигляд:

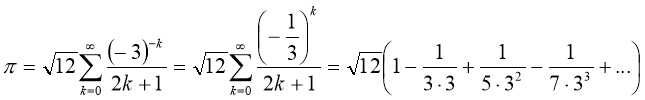
Мадхава зміг розрахувати ,  як  3.14159265359, що правильно з точністю до 11 десяткових цифр.

          Перший  значний  європейський  внесок з часів  Архімеда  зробив  німецький математик  Рудольф  ван  Цейлен  (1536—1610 р.).  Він витратив десять років на обчислення  числа  з  20-ма  десятковими  цифрами  (цей результат був опублікований у 1596 році).  Застосувавши  метод  Архімеда,  він  довів подвоєння  до n-кутника,  де  n=60·2²⁹.   Виклавши свої результати в творі «Про коло»  («Van  den  Cirkel»),   Цейлен  закінчив  його  словами: «У кого є бажання,  хай  іде  далі». Після смерті в його рукописах було виявлено ще 15 точних цифр числа . Цейлен  заповів, щоб знайдені ним знаки були висічені на його надгробному камені. На  честь  його  число іноді називали «Рудольфовим числом». 

          В 1706  Джон  Мечин  був  першим,   хто розрахував 100  десяткових цифр числа , використовуючи ряди arctg х  у формулі:

 

де

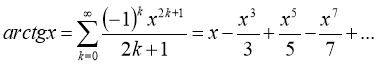
Розклавши арктангенс у ряд Тейлора, можна отримати ряд, що швидко збігається і придатний для обчислення числа π з більшою точністю. Ейлер, автор позначення π, отримав 153 правильних  знаки.

           У 1873 році англієць В. Шенкс, після 15 років праці, обчислив 707 знаків; щоправда, через помилку тільки перші 527 з них були правильними. Щоб запобігти подібних помилок, сучасні обрахування такого роду здійснюються двічі. Якщо результати збігаються, то вони зі значною ймовірністю правильні. Помилку Шенкса було виявлено у 1948 році одним із перших комп'ютерів, ним же за декілька годин було вирахувано  808 знаків π.

                                                                               

РОЗДІЛ  2

ТЕОРЕТИЧНА  ЧАСТИНА  ПРОВЕДЕНОГО   ЕКСПЕРИМЕНТУ

2.1.  Опис  та  пояснення    проведеного  експерименту

          Мабуть,  найбільш  оригінальний і несподіваний спосіб для  наближеного обчислення числа π полягає в наступному. Взявши  швейну голку                      (7 сантиметрів)  відламуємо  її  вістря,  щоб голка була рівномірної товщини.  Отримуємо  голку  завдовжки  5  сантиметрів.   Проводимо  на  аркуші паперу ряд тонких паралельних ліній,  які  знаходяться одна від одної на  однаковій   відстані,  враховуючи  при  цьому,  щоб  довжина  голки  l  задовільнила співвідношенню l ≤ h, де h - відстань  між  паралельними  прямими ( Рис. 2.1). 

          Потім  довільно   кидаємо  з деякої висоти   ( 40 – 60 см.)   голку  на виготовлене  поле ( Додаток Б ) і відмічаємо, перетне  вона  чи ні   одну  з ліній  за  різних  умов  розташування  паралельних  прямих  ( у кожному досліді, для   визначення більш    точної  умови   знаходження  π експериментальним шляхом,   змінюємо   розташування прямих  відносно  експериментатора  та   відстань  між ними).  

 

    

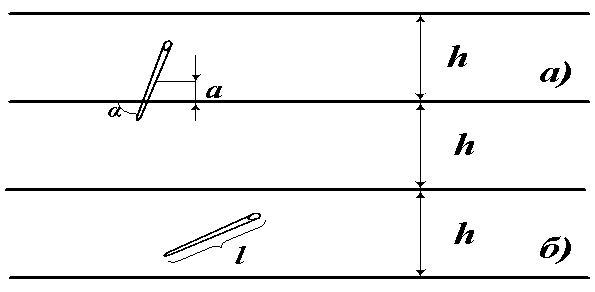
Рис.   2.1

                          

           Кожну  партію  кидків    повторюємо  по  три  рази,  підраховуючи  кількість  перетинів  голки   з  паралельними  лініями ( перетином  необхідно  вважати  і  той  випадок,  коли  голка  лише  торкається  до  накресленої  лінії )  та  загальну  кількість  кидань.  Після  цього обчислюємо   частоту  перетинів,  тобто  відношення  числа  m  кидків,  при  яких  відбувся  перетин, до  їх  загальної  кількості  n.  Достатньо   швидко  стає помітно,  що  при  багаторазовому  повторі  кидків  голки,  частота  перетинів   буде  змінюватися  все  менше  й  менше.  Більш  того,  якщо  відтворити  велику  кількість тривалих  серій  підкидань,  виявиться,  що  частота  перетинів  майже  в  усіх  серіях  буде  приблизно  тією  самою.

             Ця   властивість  «стійкості»  частоти   ( мається  на  увазі  випадковість  або  непередбачуваність  результату   кожного  досліду  )  характерне  для  всіх експериментів,   які  розглядаються  в  теорії ймовірностей.   Кожному результату такого експерименту  співвідноситься  деяке  число  р,   0  ≤  р ≤ 1 – ймовірність цього результату, що виражає ступінь можливості  появи  даного результату  в наслідок   експерименту.  Ймовірність – це якраз і є те значення, близько якого коливається  частота  здійснення  тієї  чи  іншої  події  в  достатньо  довгих  серіях  експерименту.  Тому наближене значення ймовірності можна отримати емпірично,  обчисливши  відповідну  частоту.         ( У експерименті наближення  частоти до якогось граничного значення  (ймовірності)  описує, так званий, закон великих чисел,  доведений в своїй найпростішій формі близько трьохсот років тому Якобом Бернуллі.) З іншої  сторони,  методи теорії ймовірностей у багатьох випадках дозволяють, виходячи з умов проведення експерименту, розраховувати ймовірності теоретично.

 

           

  2.2. Знаходження  ймовірності  р, для  перетину  однієї  з  паралельних  прямих  та  виведення  формули  для  підрахунку  π

 

           Для  того  щоб  пояснити,  як  підрахувати  ймовірність  перетинів  голки  та  однієї  з  паралельних  прямих,  позначимо  відстань від  цента  голки  до ближчої  прямої  через  а  (0 ≤ а ≤ ),  а  кут  між  голкою  і  прямою – через α       ( 0 ≤ α ≤ ).  Тоді,  як  зрозуміло  з  малюнка  ( Рис. 2.2 ),  умову  перетину

 голки  і  прямої  можна  записати  у  вигляді:                    

   а ≤ sin α.

            Кожному  можливому  результату  мого    експерименту  відповідає  точка  на  площині  з  координатами  ( а; α ), розташована  всередині  прямокутника,  обмеженого  координатними  осями  і  прямими  а =   і  α = (Рис. 2.2.).

 

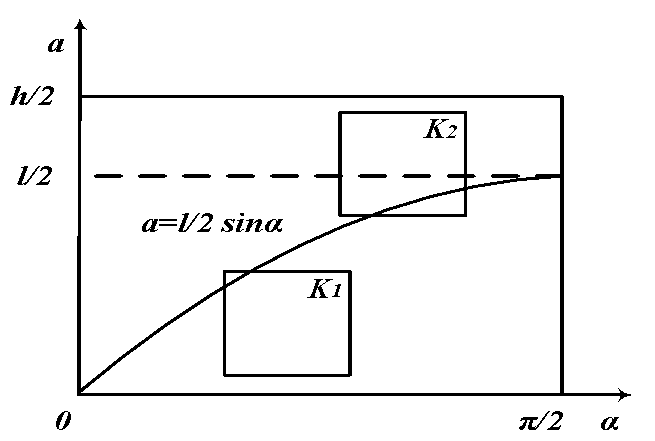
Рис.  2.2

          Таким чином, точки прямокутника,  розташовані   під  кривою  а = sin α,  відповідають  випадковостям  перетину  голки  з  прямою;  точки,  які  знаходяться  вище  даної  кривої -  випадкам,  коли  перетин  не  має  місця.  Тепер  цю ж  задачу  можна  сформулювати  по  іншому:  в  прямокутнику    навмання  вибирається  точка,  яка  ймовірність  того,  що  ця  точка  опиниться  під  синусоїдою   а = sin α?

         Слово  « навмання »  замінює  тут  вимогу  рівноправності  всіх  положень  голки,  що  впала.  Тобто  ймовірність  попадання  вибраної  точки  в  будь – який  квадрат    (α₂ – α₁ = a₂ – a₁ = d) з  даною  стороною  не  залежить    від  положення  цього  квадрата  всередині  прямокутника ( хоча  залежить  від  довжини  d  його  сторони ). Наприклад,  ймовірність  того,  що  точка  опиниться  всередині  квадратів  К₁  або  К₂  ( Рис. 2.2 )   однакова.  Звідси  не  складно  зробити  висновок,  що  можливість  потрапляння  всередину  будь – якої    фігури, розташованої  в  нашому  прямокутнику,  пропорційна  її  площі  і,  як  наслідок,  дорівнює  відношенню  цієї  площі  до  площі  всього  прямокутника. 

        Тобто  площа  криволінійної  трапеції,  обмеженої  розглянутою  синусоїдою,  дорівнює:

S_{1 =}   × sin α × d × α =  ( ( - cos ) – ( - cos 0 ) ) = .

А  так  як  площа S прямокутника  дорівнює  ,  для  шуканої  ймовірності  отримуємо  значення: 

р = = .

       Оскільки  частота  перетинів    приблизно  дорівнює ймовірності  р,  то  для  наближеного  значення  π  маємо  формулу:

π = .

 

2.3.  Підрахунок   неминучої   похибки  в  отриманих   результатах

 

          На  мою  думку,  при  проведенні  будь – якого  досліду  необхідно  враховувати  похибки. В  моєму  досліді  існує  декілька  пунктів,  де  похибку  майже  не  можливо  запобігти.  По – перше,  це  похибка  вимірів.  Адже,  для  того,  щоб  отримати  із  виведеної  формули  для  π  точне  значення,  мені  необхідно   знати  величини  h  та  l, точніше  їх  відношення.  Ці  данні  я  міг  отримати  тільки  в  наслідок  вимірів.  А похибки вимірювань  внесуть  свій  вклад в   похибку   визначення   π.

          Оцінимо ці похибки. Якщо  довжина моєї  голки   становить  50 мм,  така  ж  відстань між лініями.  Користуючись   звичайною  лінійкою, порівняно  легко  виміряти   обидві  потрібні  довжини  з точністю  до  0,1 мм  або 0,2%.  Тобто  стає  зрозумілим,  що  для  будь-якої  з потрібних  нам  довжин  відстань  0,1 мм є  межею  точності  вимірювань.  Однак,  застосувавши  більш  сучасні  інструменти  ( штангель – циркуль ),  я  можу  все ж  таки  виміряти  з  похибкою  0,01 мм.  Це вже  практична  границя,   зменшити  похибку  до  0,001 мм  в  такому  досліді  стає   виключно  складно.  Зміна  температури  голки  або  поверхні,  на  яку  нанесені  прямі,  на  1- 2 градуси  вже  спричинить  зміни  розмірів   на  величину   приблизно  0,001  мм.     Деформація  голки  при   ударі  об  поверхню,   стирання   її  кінців,  деформація  самої  поверхні  -  всі   ці  причини  роблять  проведення  експерименту  на  рівні  похибки   в  0,001 мм  неможливими.  Тому,  і  не  роблячи  більш  детальної  оцінки,  можна  впевнено  зазначити,  що  в  описаних  дослідах  число  π  могло  б  визначатися  з  похибкою,  не  менш  ніж  0,2 – 0,02 %.  Тобто,  в  моїх  дослідах  більш – точне  значення  може  сягати  лише  π =  3,141 ± 0,0006.

            Отримати  для  π  із  подібних  дослідів   величину  з  похибкою  у  восьму значущу  цифру  так  же  неможливо,  як  неможливо  зважити  сірник  на  вагах,  які  призначені  для  зважування  залізничних вагонів -  занадто  грубі  інструменти.

            Після  проведення  ряду  експериментів  та  отримання  результатів необхідно  буде  врахувати  значення  похибки.  Тому  записуючи  знайдені  значення    π,    я  приводжу  результат  з  тією  кількістю  знаків,  яка відповідатиме   підрахованій  похибці. 

          Якщо  отримавши  для  π  в  результаті вимірів  та  обчислень  значення     π = 3,149659,  а  точність  досліду  сягала  лише  1%,  тоді  варто  було б  писати  π = 3,14,  перекресливши   всі  наступні  цифри,  які   відображають  тільки  точність  обчислювального приладу,  а  не  результат    реального  досліду.  Виписувати  в  таких  випадках  всі  знаки,  які  можна  підрахувати, - це  свідомо  намагатись  обдурити  самого  себе  та  інших,  перебільшуючи  реальну  точність  дослідів.    

            Для  того,  щоб  ймовірність  перетину  дійсно  дорівнювала  теоретичному  значенню  р = ,  всі  положення  впавшої  голки  відносно  ліній  на  поверхні  повинні  бути  абсолютно  рівноправні,  тобто  жодне  з  них  не  повинно  зустрічатись  частіше  інших  (  більш  точне  формулювання цієї  вимоги  я  зазначав  при  підрахунку  р ).  Тому,  є  всі  підстави    припускати,  що  в  реальному  експерименті  досягнути  такої  умови  важко.  ( Намагаючись  досягнути  цієї  умови  я  збільшую  висоту  з  якої  падатиме  голка. )     

            Зауважу,  ще  одне  джерело  похибки  в  дослідах  такого  типу.  В  незначній  частині  випадків  падіння  голки  (  приблизно  0,1 – 0,2 % від  загального  числа  підкидань )  відстань  від  кінця  голки  до  прямої  буде  менше  0,1  мм.  В  таких  випадках  око  не  розпізнає,  відбулося  перетинання  або  ні.  Ця   обставина  може  внести  свою,  хоч  і  малу,  в  порівнянні з  іншими  похибку.

 

 

РОЗДІЛ  3

                 ПРАКТИЧНА  ЧАСТИНА  ПРОВЕДЕНОГО  ЕКСПЕРИМЕНТУ

     

       3. 1.  Дослід  І

 

        У  першому  досліді  я  кидатиму  голку  на  самостійно  зроблений  експонат,  поклавши  його  на рівну  поверхню   так,  щоб  паралельні  прямі  були   перпендикулярно  розташовані  відносно  моєї  руки  ( Додаток В ).  Проводжу  три  партії  кидань  голки  та  підраховую   значення  π.  Заношу  всі  данні  до  табл.  3.1.

 

                                  Таблиця 3.1

Результати  першого  проведеного  досліду

Порядковий  №  досліду	H   ( мм )	l   ( мм )	Число кидань	Число  перетинів	Експериментальне       значення   π
1	70	50	968	416	3,324…
2	50	50	1074	657	3,269…
3	100	50	2037	649	3,1386…
Істинне  значення  π  з  вісьма   знаками :                                  3, 1415926

 

h – відстань  між  паралельними  прямими;

l – довжина  голки.

         У  даному  досліді,  виконавши   деякі  дії,   я  самостійно  отримав  три  значення  для  π.   Найбільш  точне   підраховане  значення     π = 3,1386…

 

 

  

      3. 2.  Дослід  ІІ

 

       У   другому  досліді  я  кидатиму  голку  на  експонат  поклавши  його   на  рівну  поверхню  так,   щоб   паралельні  прямі   були   розташовані  паралельно  відносно  моєї  руки  ( Додаток  Г ).   Проводжу  три  партії  кидань  голки  та  підраховую   значення  π  за  раніше  виведеною  формулою.  Заношую  всі  данні  до  табл.  3. 2.

 

                                                                                                                  Таблиця  3.2

Результати    другого  проведеного  досліду

Порядковий  №  досліду	h  ( мм )	l  ( мм )	Число кидань	Число  перетинів	Експериментальне       значення   π
1	70	50	579	264	3,1213…
2	100	50	3048	969	3,1455…
3	50	50	921	577	3,1923…
Істинне  значення  π  з  вісьма   знаками :                                  3, 1415926

 

h – відстань  між  паралельними  прямими;

l – довжина  голки.

         У  даному  досліді  виконавши   деякі  дії   я  самостійно  отримав  три  значення  для  π.   Найбільш  точне   підраховане  значення     π = 3,1455…

 

ВИСНОВКИ

Математика  цікава   не  тільки  своїми  формулами,  теоремами,  аксіомами  та  задачами,  а  й  історією  їх  виведення  та  отримання.  Так,  наприклад,  шлях  знаходження  значення  π  є  дуже  довгим  та  різноманітним  у   кожній  стародавній державі.  Перші  методи  обчислення  цього  значення,  приміром,   були  описані у  Вавилоні  та  Єгипті.   Дійшли  вони  до  нас  тільки  завдяки  тому,  що  були нанесені  на  глиняні  дощечки  та  стіни  скель.  Зараз  же  історичну  інформацію  можна  знайти  в  публікаціях  Марта  Бурляйа,  А. Н.  Зайделя.   У   бібліотеках  міста  Харкова,  користуючись  довідниками   та  посібниками  до  радянського,   радянського  періоду та сучасності  таких,  як  «У  світі  математики»,  «История  математики»,  «Математика  после  уроков»  я  знайшов  купу  корисної  та  необхідної  інформації.

            Знаходячи  число  π  за  допомогою  теорії  ймовірностей    можна  зробити  висновок,  що  розв’язок  математичної  задачі    може  ґрунтуватися  не  лише  на  теоретичній  основі  або  на  практичних  вимірах,  а  й  на  експериментах. 

           У   роботі  я  використав  власноруч  зроблене  для  кидання  голки  поле  з  нанесеними  на  нього паралельними  прямими  і  голку.  При  проведенні  першого  досліду  лінії  були  розташовані  перпендикулярно  до  руки  дослідника.  У  другому  досліді  нанесені    прямі  були  паралельні  до  моєї  руки.

            Провівши  два  досліди,  та  порівнявши  їхні результати,  я одержав  умову  для  знаходження  більш  точного  значення числа π, а саме:  найбільш  наближений  результат ,   π= 3,1455 … ,  я  отримав   під  час  другого досліду при  умові,  коли  паралельні  прямі  були  розташовані  вертикально   відносно  мого  тіла.   Це,  мабуть,  було  спричинено  особливістю  розташування  руки.  Адже,  під  час  кидання  голки  за  такої  умови   рука  була  розташована  паралельно  лініям,  а , як  наслідок ,    голка  також  перед  киданням  була  розташована  подібним  чином.   Ураховуючи,  що  закручення  голки  (  за  фізіологічною  будовою  руки )  відбувалось  у  більшості  випадків,  приблизно,   на  140⁰ - 180⁰   можливість  перетину  зменшувалась  (  якщо  оберт  відбувався  на  180⁰ , то  голка  розташовувалась  би  паралельно  у  70 – 89 %  випадках).   Якщо  взяти  голку  перпендикулярно  руці,  то  при  її  оберті  виникнуть  незручності. 

           Таким  чином,  в  першому  досліді  ймовірність  перетину  була  більшою,  що  й  не  давало   наблизитись  з  більшою  точністю  до    значення  π.

         Тому,  для  знаходження  якомога   більш  точного  значення  числа   π  експериментальним  шляхом  за  допомогою  теорії  ймовірності,   необхідно  дотримуватися  умови,  коли  довжина  голки  l  задовольняє   нерівність  l ≤ h,  де   h  -  відстань  між  паралельними  прямими,  кидання  голки  робити  з  висоти    40 – 60  см,  а  паралельні  прямі  при  цьому  повинні  бути  розташовані   вертикально  відносно  тіла  експериментатора  та  паралельно  його  руці  (  Додаток  Г ).

         Для  проведення  практичної  частини  експерименту  я  витратив           16,8   годин   ( 8627 × 7с ≈ 60389 с ).

           При  проведенні  дослідів  мною  було  помічено,  що  точність  наближення  в  формулі   π =   буде  тим  вище,  чим  більша  n  ( загальна  кількість  підкидань голки ).   Спробувавши   виконати   даний   експеримент  я  виявив,  що  отримати   цим  методом  значення  3, 1   досить легко,  але  знайти  наступний десятковий знак  - 4 - вже значно важче.

           У  ХІХ  столітті,  коли  теорія  ймовірностей  найчастіше  розглядалась,  як  напівекспериментальна  наука,  подібні  досліди  мали  більше  значення  й  досить  ретельно  проводились  багатьма  вченими. Для  порівняння,  в               Табл. 1  наведено  прізвища  вчених  та  результати,  які  вони  отримали  при  киданні  голки  на  площину  з  паралельними  прямими,  що  розташовувались  горизонтально  відносно  експериментатора.

         Порівнюючи  значення  π,   які  наведені  в  табл.  1,  з  результатами  моїх  досліджень  та   значенням  числа,  отриманого  за  допомогою  обчислювальної  техніки,  бачимо,  що   майже  в  усіх    випадках   значення  відрізняються  від  числа  π  на  0,01 – 0,03.    Така  розбіжність  у  результатах  спричинена  похибкою  вимірювань  (  види  та джерела  похибок  були  описані  мною  в  Розділі  2 ).           

                                                                                                                        Таблиця 1

Результати,  які  були  отримані   вченими  в  задачі  Бюффона

Експериментатор	Рік  проведення  експерименту	Число  підкидань	Експериментальне  значення  π
Вольф Сміт Фокс Де Морган Лаззеріні Рейна   Гриджеман	1850 1855 1894 1860 1901 1925 1960	5000 3204 1120 600 3480 859 2	3,1596    3,1553    3,1419    3,137    3,1415929    3,1795    3,143
Істинне значення  π  з  вісьма  знаками                                   3,1415926

 

        Чудовий  результат   дослідів  у  Лаззеріні    та  Фокса,  в  більшій  мірі  зобов’язаний  майстерній  зупинці  дослідів  у  найбільш  сприятливий    момент  разом  з  великою  вдачею.  У  випадку  з  Лаззеріні,  коли  оцінка  числа  π      вже  була  відома,  приблизно,  близько  дев’яти   точних  знаків  після  коми,  можливо  мало  місце  саме  подібне  вміле  припинення  експерименту.  Якщо  б  точне  значення  π  не  було  відоме  до  експерименту,  так  щоб  зупинка  в  сприятливий  момент  не  мала змоги  бути  використана,  то  мабуть,  знаходження  відношення  довжини  кола  до  його  діаметра  за  допомогою  проведення   вимірів  сантиметром  були б  більш  точні.

         Але  не  зважаючи  на  неточність  отриманих   результатів,  на  мою  думку,  проводячи  такі  дослідження  учні  старших  класів,  все рівно,  мають  змогу  застосувати  набуті  знання  з  теорії  ймовірностей    та  інтегрального  обчислювання  на  практиці, що  є  також  важливим.  

СПИСОК   ВИКОРИСТАНИХ  ДЖЕРЕЛ

1. Глейзер  Г. И.  История  математики  в  школе. – Москва: Просвещение, 1982.- С. 97 – 99.

2. Клейнер Г. М.,  Клейнер Л. М.,  Математика  и  научная  картина  мира.- К.: Рад.  шк., 1984. – С. 23- 44.  

3. Литлвуд  Дж., Математическая  смесь: Пер. с англ. – 5-е изд., - испр. – М.: Наука. Гл. ред. физ. мат.  лит., 1990. – С. 54 – 57.

4. Перельман  Я. И. Занимательная  геометрия.: издание  десятое, стереотипное. – Л.: Гос.  изд. физ. мат. лит. – Москва, 1958. – С. 194 – 201.

5.  Кандал М.,  Поран П.  Геометрические  вероятности. – Москва: Наука, 1972.-С. -  82 – 84.

6. Мостеллер  Ф.  Пятьдесят  занимательных  задач  с  решением. – Л.: Наука, 1985. -  С. 81 – 83.

7.  Кольман  Э. История  математики  в  древности. – Л.: Гос.  изд.  физ.  мат. лит., 1961. – С. 57 – 60.

8. Балк  М. Б. Балк  Г.  Д.  Математика  после  уроков:  Пособие  для  учителей. – Л.: Просвещение, 1971. – 289 – 297.

9. Зайдель  А. Н. Обман  или  заблуждение? ( Об  одном  способе  вычисления    π ) // Квант. – 1983. - № 5. – С. 24 – 27.

ДОДАТКИ

                       Додаток  А

Правильні  багатокутники  вписані  і описані  навколо  кола.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток  Б

Власноруч  виготовлене  поле  для  кидання  голки  і  запобігання  її  втрати.

 

 

 

 

 

 

 

 

Додаток  В

 

              Положення  руки,   розташованої  перпендикулярно  лініям. 

 

 

 

Додаток  Г

Положення  руки,   розташованої  паралельно  лініям.