Проектна робота "Похибка при топографічних зйомках та її оцінка"

Проектна  робота

 

 

 

 

 

 

ПОХИБКА ПРИ ТОПОГРАФІЧНИХ ЗЙОМКАХ

 ТА ЇЇ ОЦІНКА

 

 

 

Роботу виконав: Чорток Микита Михайлович, учень 11-Б класу Харківської гімназії № 43 Харківської міської ради Харківської області

Науковий керівник: ШептурГалина Євгенівна, учитель математики Харківської гімназії № 43 Харківської міської ради Харківської області

 

 

 

 

Харків – 2018

 

 

 

Зміст

 

Вступ            4

1. Теоретичні основи вивчення похідної та рядів Тейлора    6

1.1 Історія вивчення похідної        6

1.2 Застосування похідної в практичній діяльності    9

1.3 Історія вивчення рядів Тейлора       10

2. Похибка при топографічних зйомках та її оцінка     13

Висновки            16

Список використаних джерел        17

 

 

Вступ

«[Математика — це]… велике місто, передмістя якого не перестають розростатися дещо хаотично, у той час як центр періодично перебудовується, додержуючи щоразу все чіткішого плану і прагнучи до величнішого розташування, у той час як старі квартали з їх лабіринтом провулків зносяться для того, щоб прокласти до околиці вулиці, все пряміші, все ширші, все зручніші».

Ніколя Бурбакі , група французьких математиків

 

Актуальність дослідження: при вивчення похідної в шкільному курсі математики розглядаються деякі її застосування у фізиці, а також ряд текстових завдань на знаходження найбільшого або найменшого значень. Однак сфера застосування похідної цим не обмежується. Наприклад, існує маса реальних економічних завдань, для вирішення яких необхідно використовувати методи диференціального числення.

Кожна людина час від часу опиняється в ситуації, коли треба відшукати найкращий спосіб вирішення будь-якої задачі, і математика стає засобом вирішення проблем організації виробництва, пошуків оптимальних рішень. Важливою умовою підвищення ефективності виробництва і поліпшення якості продукції є широке впровадження математичних методів в техніку. Серед завдань математики велику роль відводять завданням на екстремуми, тобто завданням на відшукання найбільшого і найменшого значення, найкращого, найбільш вигідного, найбільш економного. З такими завданнями доводиться мати справу представникам різних спеціальностей: інженери-технологи намагаються так організувати виробництво, щоб вийшло якомога більше продукції, конструктори хочуть так спланувати прилад на космічному кораблі, щоб маса приладу була найменшою, економісти намагаються спланувати прикріплення заводів до джерел сировини так, щоб транспортні витрати виявлялися мінімальними.

Об’єкт дослідження: теоретико-методичні підходи до визначення похідної та її застосувань.

Предмет дослідження: механізм використання методів математичного аналізу в різних галузях науки і техніки.

Мета роботи: розробити практичні рекомендації щодо застосування методів математичного аналізу (адже не тільки похідної, а, наприклад, рядів) для визначення відстані на топографічній карті між двома пунктами Земної поверхні.

Завдання: 1) розглянути сутність похідної та рядів Тейлора; 2) розглянути застосування похідної в практичній діяльності; 3) показати застосування похідної в різних галузях; 4) розширити існуючу методичну базу використання похідної в практичні діяльності.

Методи дослідження: теоретичне узагальнення, системно-структурний метод, аргументації та абстрагування, аналітичний та економіко-статистичний, групування, графічний та картографічний методи.

Наукова новизна отриманих результатів та особистий внесок автора полягають у комплексному дослідженні методичних підходів застосування похідної в різних галузях науки і техніки. Найбільш суттєві результати, які характеризують новизну дослідження полягають в удосконаленні науково-методичного підходу до визначення на основі степеневих рядів Тейлора відстані на топографічній карті між двома пунктами Земної поверхні.

 

 

• Теоретичні основи вивчення похідної та рядів Тейлора

 

• Історія вивчення похідної

 

Похідна – одне з фундаментальних понять математики.  Це поняття  виникло в XVII н.. у зв’язку з необхідністю розв’язання багатьох задач з фізики, механіки і математики, у першу чергу наступних двох: визначення швидкості прямолінійного нерівномірного руху і побудови дотичної до похідної плоскої кривої.

Перша з цих задач була уперше вирішена Ньютоном. Функцію він називав флюентою, тобто поточною величиною (від латинського fluere – текти), похідну ж – флюксіей (від того ж fluere). Ньютон позначав функції останніми літерами латинського алфавіту u, x, y, z, а їх н.сій, тобто похідні від н.сі за часом, - відповідно тими ж літерами з крапкою над ними: 

Ньютон прийшов до поняття похідної, виходячи з питань механіки. Свої результати в цій області він виклав у трактаті, названому «Метод н.сій і нескінченних рядів», що був складений близько 1671 р. Припускають, що Ньютон відкрив свій метод н.сій ще в середині 60-х років XVII н.., однак вищезгаданий його трактат був опублікований посмертно лише в 1736 р.

Математиків XV – XVII н.. довго хвилювало питання про перебування загального методу для побудови дотичної в будь-якій точці кривої. Задача ця була пов’язана також з вивченням рухів тіл і з відшуканням екстремумів найбільших і найменших значень різних функцій.

Деякі окремі випадки вирішення задач були отримані ще в стародавності. Так у «Початках» Евклід представив спосіб побудови дотичної до кола, Архімед побудував дотичну до спіралі, що носить його ім’я, Аполлоній – до еліпса, гіперболи і параболи. Однак давньогрецькі вчені не вирішили задачу до кінця, тобто не знайшли загального методу, придатного для побудови дотичної до будь-якої плоскої кривої в точці її похідної.

Із самого початку XVII в. чимало вчених, у тому числі Торрічеллі, Вівіани, Роберваль, Барроу, намагалися знайти вирішення питання, вдаючись до кінематичних міркувань. Перший загальний спосіб побудови дотичної до алгебраїчної кривої був викладений у «Геометрії» Декарта. Більш загальним і важливим для розвитку диференціального числення був метод побудови дотичних Ферма.

Ґрунтуючись на результатах Ферма і деяких інших висновках, Лейбниц значно повніше своїх попередників вирішив задачу, про яку йде мова, створивши відповідний алгоритм.

Позначення у′ та f′ для похідної ввів Лагранж. Сам термін «похідна» уперше зустрічається у француза Луа Арбогаста в його книзі «Обчислення похідних», опублікованої в Парижі в 1800 р. Цим терміном відразу ж став користуватися і Лагранж. Термін цей швидко ввійшов у загальний ужиток, а Коші, використовуючи початкову літеру цього терміна, став позначати похідну символом D_y або D_f(x).

Перший друкований курс диференціального числення вийшов у світ в Парижі в 1696 р. під заголовком «Аналіз нескінченно малих». Його автор Г. Ф. Де Лопиталь за основу цієї книги взяв рукопис Йоганна Бернуллі, одного з найближчих співробітників Лейбница. Ось чому цей курс варто розглядати як типовий здобуток школи Лейбница.

Поняття похідної – фундаментальне поняття математичного аналізу, за допомогою якого досліджують процеси і явища в природничих, соціальних і економічних науках. Вивчення різних  процесів (механічного руху, хімічних реакцій,  розширення рідини при нагрівання, значення електричного струму та н..) проводять до необхідності обчислення швидкості зміни різних величин, тобто до поняття похідної.

До поняття похідної приводять такі задачі: задача про швидкість прямолінійного руху, задача про густину неоднорідного стержня, задача про силу струму, задача про теплоємність, задача про дотичну до кривої.

Розглянемо задачу про дотичну до кривої. Нехай крива в прямокутній системі координат хОу задана рівнянням у=f(x), є неперервною, визначеною в деякому околі точки х₀ і має невертикальну дотичну в точці Р(х0, f(x0)). Знайдемо кутовий коефіцієнт цієї дотичної (рис. 1.1).

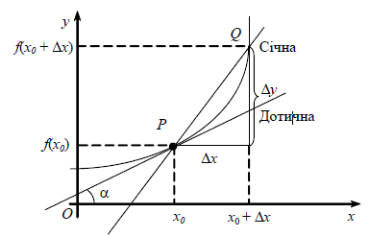
Рисунок 1.1

 

Нехай Δу=f=f(x₀+Δx)–f(x) – приріст функції у=f(x) в точці х₀, що відповідає приросту незалежної змінної х (рис. 1). Проведемо січну РQ і позначимо через кут φ, утворений цією січною з додатним напрямом осі Ох.

З графіка видно, що кутовий коефіцієнт січної РQ дорівнює:

 

    (1.1)

 

Якщо x 0 , то точка Q прямує до точки Р вздовж кривої у=f(x), а січна РQ, повертаючись навколо точки Q, переходить в дотичну. Кут φпри цьому прямує до деякого граничного значення . Отже, кутовий коефіцієнт дотичної дорівнює

.    (1.2)

Відношення приросту f функції у=f(x) до приросту Δx незалежної змінної х називається диференціальним відношенням:

 

      (1.3)

 

Якщо відношення має границю при x 0 , то ця границя називається похідною функції f в точці x₀  і позначається f’(x₀):

 

.    (1.4)

 

• Застосування похідної в практичні діяльності

 

Похідна знайшла широке застосування в практичні діяльності. Одним з прикладів є її використання в геодезії.

В курсі геометрії зазначено спосіб визначення висоти предмета за допомогою кутомірних інструментів. При топографічних зйомках місцевості аналогічний прийом використовується для визначення перевищення однієї точки земної поверхні над іншою. Цей спосіб дає хороший результат, якщо розглянуті точки знаходяться на незначній відстані. В іншому випадку починає позначатися кривизна Землі і виникає суттєва похибка.

Якщо відстань між точками B і C досить велика, то до знайденого (за допомогою кутомірних інструментів) значення підвищення точки B над точкою C додають так звану поправку на кривизну Землі:

 

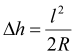      (1.5)

 

де R – радіус Землі, l – довжина горизонтальної проекції відрізка BC.

 

Доведемо зазначену вище формулу для поправки Δh. Розглянемо рис. 1.2, на якому штрихами зображена поверхню океану, точка O – центр Землі.

 

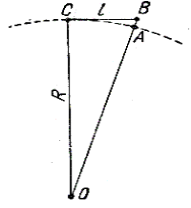
Рисунок 1.2

Нехай точка C лежить на поверхні океану, а точка B належить горизонтальній площині, що проходить через точку C. Так як в такому випадку кут між променем CB і горизонтальним напрямком (він визначається за допомогою схилу) дорівнює нулю, то з точки C нам здасться, що точки B і C мають однакову висоту. Погодившись з цим, ми допустимо похибку hABOBOA .

Величина l відносно мала в порівнянні з R. Тому для обчисленняможна скористатися наближеною формулою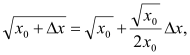отриманою за допомогою похідної. Замінивши в цій формулі , ми отримаємо вказаний вище вираз для h.

 

1.3 Історія вивчення рядів Тейлора

 

Грецький філософ Зенон розглядав проблему знаходження нескінченного ряду для досягнення кінцевого результату, але відхилив його як неможливе: результатом був парадокс HYPERLINK "https://uk.wikipedia.org/wiki/%D0%90%D0%BF%D0%BE%D1%80%D1%96%D1%97_%D0%97%D0%B5%D0%BD%D0%BE%D0%BD%D0%B0"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%90%D0%BF%D0%BE%D1%80%D1%96%D1%97_%D0%97%D0%B5%D0%BD%D0%BE%D0%BD%D0%B0"Зенона (Зенон розкрив протиріччя, в які впадає мислення при спробі осягнути нескінченне в поняттях його апорії — це перші парадокси, що виникли у зв'язку з поняттям нескінченного). Пізніше Аристотель запропонував філософський розв'язок парадоксу, але математичний зміст очевидно не було розв'язано, поки не був отриманий Архімедом, як це було зроблено до Аристотеля атомістом Демокрітом. Саме завдяки методу HYPERLINK "https://uk.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B2%D0%B8%D1%87%D0%B5%D1%80%D0%BF%D1%83%D0%B2%D0%B0%D0%BD%D0%BD%D1%8F"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B2%D0%B8%D1%87%D0%B5%D1%80%D0%BF%D1%83%D0%B2%D0%B0%D0%BD%D0%BD%D1%8F"вичерпування Архімеда, нескінченне число прогресивних підрозділів може бути виконане для досягнення кінцевого результату. Лю Хуей залежно використав аналогічний метод декілька століть потому.

Числовим рядом називається нескінченна послідовність величин, сполучених знаками додавання:

 

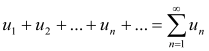,     (1.6)

 

де u_n – загальний член ряду.

 

Якщо функція f(x) нескінченне число разів безперервно диференційована в околі точки x=a і залишковий член у формулі Тейлора прямує до нуля при необмеженому зростанні n, то в околі цієї точки функцію f(x) можна розвинути в ряд Тейлора:

 

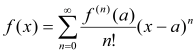     (1.7)

 

У 14-му столітті, найбільш ранні приклади використання рядів Тейлора і тісно пов'язані методи були дані Мадхаве з Сандамаграми. Хоча жоден звіт про його роботу не уцілів, праці пізніх індійських HYPERLINK "https://uk.wikipedia.org/w/index.php?title=%D0%86%D1%81%D1%82%D0%BE%D1%80%D1%96%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8_%D0%B2_%D0%86%D0%BD%D0%B4%D1%96%D1%97&action=edit&redlink=1"  HYPERLINK "https://uk.wikipedia.org/w/index.php?title=%D0%86%D1%81%D1%82%D0%BE%D1%80%D1%96%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8_%D0%B2_%D0%86%D0%BD%D0%B4%D1%96%D1%97&action=edit&redlink=1"математиків свідчать про те, що він виявив ряд особливих випадків ряду Тейлора, у тому числі для тригонометричних HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D1%96_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D1%96%D1%97"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D1%96_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D1%96%D1%97"функцій синуса, косинуса, тангенса і арктангенса. Керальска школа астрономії і математики надалі розвивала його роботи з різними рядами розширення і раціональних наближень до 16-го століття.

Концепція ряду Тейлора була сформульована шотландським математиком Джеймсом HYPERLINK "https://uk.wikipedia.org/wiki/%D0%94%D0%B6%D0%B5%D0%B9%D0%BC%D1%81_%D0%93%D1%80%D0%B5%D0%B3%D0%BE%D1%80%D1%96"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%94%D0%B6%D0%B5%D0%B9%D0%BC%D1%81_%D0%93%D1%80%D0%B5%D0%B3%D0%BE%D1%80%D1%96"Грегорі і офіційно представлена англійським математиком Бруком Тейлором в 1715 році. Якщо ряд Тейлора з центром в нулі, то цей ряд також називається рядом Маклорена , який названий на честь шотландського математика Маклорена, що широко використав цей особливий випадок ряду Тейлора в 18-му столітті.

Функція може бути апроксимована за допомогою скінченного числа членів ряду Тейлора. Теорема Тейлора дає кількісні оцінки похибок, які вносяться за допомогою використання такого наближення. Поліном, утворений з деяких початкових членів ряду Тейлора, називається многочленом HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A2%D0%B5%D0%B9%D0%BB%D0%BE%D1%80%D0%B0"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A2%D0%B5%D0%B9%D0%BB%D0%BE%D1%80%D0%B0"Тейлора. Ряд Тейлора функції є границею поліномів Тейлора цієї функції у міру збільшення міри, за умови, що існує границя. Функція може не дорівнювати її ряду Тейлора, навіть якщо ряд збігається в кожній точці. Функція, яка дорівнює її ряду Тейлора у відкритому інтервалі (чи в колі в комплексній HYPERLINK "https://uk.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81%D0%BD%D0%B0_%D0%BF%D0%BB%D0%BE%D1%89%D0%B8%D0%BD%D0%B0"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81%D0%BD%D0%B0_%D0%BF%D0%BB%D0%BE%D1%89%D0%B8%D0%BD%D0%B0"площині), називається аналітичною в цьому інтервалі. У математиці Ряд Тейлора — представлення функції у вигляді нескінченної HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"суми доданків, які обчислюються зі значень функцій похідних в одній точці.

 

 

• Похибка при топографічних зйомках та їх оцінка

 

Топографія – в перекладі з грецької місце, місцевість (topos) + писати (grapho) – наукова дисципліна, яка вивчає методи зображення географічних і геометричних елементів місцевості і складання на їх основі топографічних карт. А топографічна карта – це великомасштабна загально географічна карта, яка з великою точністю і щонайдетальніше представляє основні природні і соціально-економічні об’єкти (рельєф, рослинність, населені пункти, дорожні мережі і т. п.). Щоб створити оригінал топографічної карти необхідно виконати сукупність робіт, що називається топографічною зйомкою.

При топографічних зйомках широко використовуються проекції лінії AB земної поверхні на площину AB₁, дотичну до земної кулі в точці A. (див. рис. 2.1).

 

Рис. 2.1

 

Одним із завдань нашого дослідження є розширення існуючої методичної бази використання похідної в практичні діяльності, а саме формування науково-методичного підходу до визначення відстані на топографічній карті між двома пунктами Земної поверхні. Отже, нам потрібно за допомогою математичного аналізу знайти на скільки відстань між точками A і B відрізняється від A і B₁ та оцінити похибку при цьому.

Відстань між точками A і B земної поверхні можна обчислити як довжину дуги великого перетину земної кулі за відомою формулою: , де R – радіус Земної кулі, α – центральний кут (в рад.).

Розглянемо трикутник OAB₁. В ньому . Позначимо AB₁, що буде на топографічній карті через l. Тоді , а кут α: . Знайдемо різницю між AB₁ і AB. Так як , то . Нехай різниця між

.

Розкладемо  в ряд Тейлора (для нашої задачі це буде ряд Маклорена, так як a=0):

…… ,

який, як відомо, буде збіжним при .

Зрозуміло, що , що і забезпечує використання цієї можливості.

Отже,  … і …)… .

Обмежуючись двома членами розкладу маємо наближену формулу для різниці між справжньою відстанню між точками на поверхні земної кулі AB і заміною її проекцією на дотичну AB₁.

 

Похибка обчислення при цьому не перевищує першого відкинутого члена ряду, тобто .

Оцінимо цю похибку, наприклад, для l < 100 км < 10⁷ см. Як відомо радіус Земної кулі R = 6,371 км або 6,410⁸ см

 (см)

А сама різниця  наближено дорівнює:

 (м).

Таким чином, нами запропонований науково-методичний підхід до визначення на основі степеневих рядів Тейлора відстані на топографічній карті між двома пунктами Земної поверхні.

За представленими розрахунками можна зробити висновок про те, що різниця між двома пунктами Земної поверхні на місцевості в 100 км і відстанню між ними на топографічній карті оцінюється в 8 м, за похибкою обчислювань, що складає менше 0,2 см. Зважаючи на природний рельєф поверхні, такими відхиленнями можна знехтувати.

 

 

 

Висновки

 

Математика є основою природних і технічних наук, без неї немислима жодна сучасна технологія. Крім того, математика активно впроваджується в економіку. Приступаючи до даного дослідження, ми ставили перед собою завдання: застосування похідної в різних сферах практичної діяльності. Для цього нами розглянуті теоретичні основи похідної, її історія та приклади обчислення; були проаналізовані особливості використання похідної у фізиці, математиці, хімії, біології, географії та економіці; а також різних сферах практичної діяльності: геодезії, в транспорті, в будівництві.

Застосування похідної досить широке і його складно повністю охопити в роботі такого типу, однак, ми спробували розкрити основні, базові моменти. В наш час, у зв'язку з науково-технічним прогресом, зокрема з швидкою еволюцією обчислювальних систем, диференціальне числення стає все більш актуальним при вирішенні як простих, так і надскладних завдань.

За допомогою математичного аналізу, а саме теорії степеневих рядів Тейлора (представлення функції у вигляді нескінченної HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"  HYPERLINK "https://uk.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"суми доданків, які обчислюються зі значень похідних функцій в одній точці) нами запропонований науково-методичний підхід до визначення відстані на топографічній карті між двома пунктами Земної поверхні.

Отримані результати засвідчили, що різниця між двома пунктами Земної поверхні на місцевості в 100 км і відстанню між ними на топографічній карті оцінюється в 8 м, за похибкою обчислювань, що складає менше 0,2 см. Зважаючи на природний рельєф поверхні, такими відхиленнями можна знехтувати.

 

 

Список використаних джерел

 

• Алгебра. 11 клас: Підруч. для загальноосвіт. навч. закладів: академ. рівень, проф.. рівень / Є. П. Нелін, О. Є. Долгова. – Х.: Гімназія, 2011. – 448 с. Режим доступу: https://vshkole.com/11-klass/uchebniki/algebra/yep-nelin-oye-dolgova-2011-akademichnij-riven-profilnij-rivni/stranitsa-2
• Бабенко С.П. Уроки алгебри, 11 кл.,-Х.:Основа, 2011.
• Дороговцев Я.В. Математичний аналіз: Підручник: У двох частинах. Частина 2. — К. : Либідь, 1994. — 304 с.
• Кузиванов Д.О. Практическое применение производной. Режим доступу: https://www.scienceforum.ru/2016/1538/23223
• Мерзляк А.Г., Полонський В.Б., Рабінович Ю.М., Якір М.С. – Х., Гімназія, 2011.
• Нелін Є.П. Алгебра і початки аналізу: підручник для 11 кл. загальноосвітніх навчальних закладів, -Х.:Світ дитинства, 2006.
• Нікулін О. В. Вища математика: факти і формули, задачі і тести : навч. посіб. / О. В. Нікулін, Т. В. Наконечна. – Дніпропетровськ : Біла К. О., 2015. – 188 с.
• Пилипенко І.М. Застосування похідної в різних галузях науки. Урок з алгебри. Режим доступу:  http://osvita.ua/school/lessons_summary/math/26033/
• Роганін О.М. Тест-контроль, алгебра, геометрія. Поточне, тематичне, річне оцінювання.-Х.: Весна, 2009.