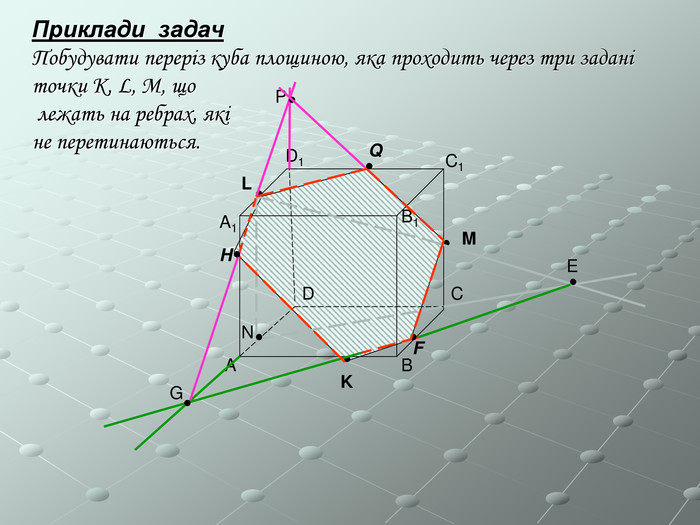
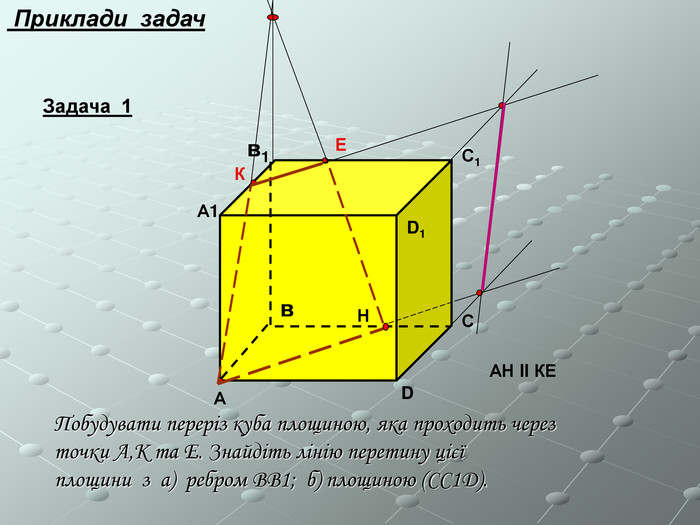
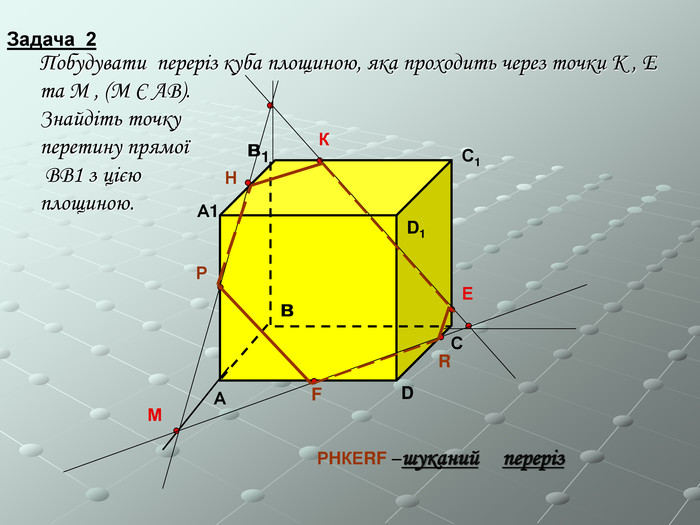
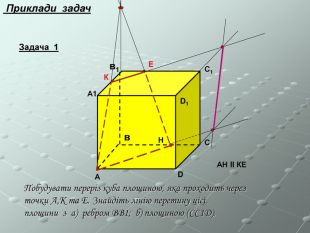
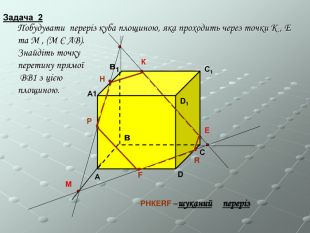
Програма спецкурсу з геометрії в 10 класі з поглибленим вивченням математики "Стереометрія в типових задачах"
Про матеріал
Презентація на тему "Програма спецкурсу з геометрії для 10 класу з поглибленим вивченням математики" буде корисна для вчителів математики. які працюють як в класах з поглибленим вивченням математики, так і в профільних класах.
Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія (профільний рівень) 10 клас (Бевз В.Г., Бевз Г.П., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку