Пропорційність при обчисленні площ многокутників

                 Пропорційність при обчисленні площ многокутників
 

 

ЗМІСТ

Вступ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1. Пропорційність при обчисленні площ многокутників.

Система опорних задач. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5

1.1. Пропорційність і площа трикутника. . . . . . . . . . . . . . . . . . . . .5

1.2. Пропорційність і площа паралелограма. . . . . . . . . . . . . . . 10

1.3. Пропорційність і площа трапеції. . . . . . . . . . . . . . . . . . . . . . 12

1.4. Пропорційність і площа довільного многокутника. . . 13

2. Розвʼязання задач з використанням властивостей площ. . . . . . . . . . . . . . . .17.

2.1. Бісектриса, медіана, висота трикутника і відношення площ. .17

2.2. Відношення площ подібних трикутників. . . . . . . . . . . . . . . . . . .23

2.3. Пропорційність і подібність в трапеції. . . . . . . . . . . . . . . . . . . . . . . 25

2.4.Пропорціональность і площа опуклого многокутника. . . . . . . . . 27

Висновки

Список використаних джерел
 

 

 

 

 

 

 

 

 

 

ВСТУП

       При розвʼязанні більшості задач з геометрії треба залучати різноманітні факти теорії, доведення тих чи інших тверджень. Але і знаючи теорію, оволодіти навичками у розвʼязанні задач можна лише розвʼязавши їх досить багато, починаючи з простих і переходячи до більш складних, а найголовніше, розумно оволодіти методами розвʼязання задач.

        Гіпотеза: оволодіння методами розвʼязання задач на пропорційність -об'єктивна допомога при розвʼязанні геометричних задач підвищеної складності.

        Актуальність дослідження обумовлена підготовкою до іспитів з математики, що вимагає поглиблення знань в усіх розділах математики.

         Робота «Пропорційність при обчисленні площ многокутників» є доповненням вивчених в шкільній геометрії властивостей площ многокутників.

        Об'єкт дослідження: опуклі многокутники.

        Предмет дослідження: пропорційність при обчисленні площ многокутників.

        Мета: вивчення теорії питання і дослідження прийомів розвʼязання

планіметричних задач з використанням властивостей площ.

Завдання: 1. Вивчити науково-методичну літературу з даної теми.

2. Зібрати опорні задачі.

3. Оволодіти різними шляхами пошуку розвʼязання задач з використанням

властивостей площ.

4. Класифікувати задачі, які розвʼязуються на знаходження відношення площ многокутників.

5. Застосувати опорні задачі для розвʼязання більш складних планіметричних задач.

 

         1 Пропорційність при обчисленні площ  многокутників.

Система опорних задач

         Площа - це число, яке ставиться у відповідність обмеженій плоскій фігурі (многокутнику).

Властивості:  1. Площа многокутників є невід'ємним числом.

2. Рівні многокутники мають рівні площі.

3. Якщо многокутник складений з двох многокутників, які не мають спільних внутрішніх точок, то його площа дорівнює сумі площ цих многокутників.

4. За одиницю виміру площі приймається площа квадрата зі стороною, що дорівнює 1 одиниці довжини.

1.1 Пропорційність і площа трикутника

          Площа трикутника обчислюється за формулою S =ah_а, де  a - довжина сторони трикутника, h_а - висота, опущена на цю сторону.

          Задача 1. Площі трикутників, що мають одну й ту саму основу, пропорційні висотам.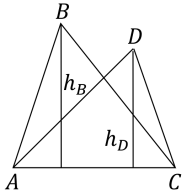

Доведення:                                        S_ABC =AC·h_B,

                   S_ADC=AC·h_D, тоді

         ==.

 

Висновок: площі трикутників, що мають рівні

сторони, відносяться як відповідні цим сторонам висоти.

Задача 2. Площі трикутників, що мають рівні висоти, пропорційні основам.

                 Доведення:   S_ABC =AC·h_B,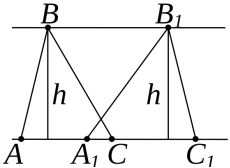  

                 =A₁C₁·h_B1, тоді

                        = .

Висновок: якщо два трикутники мають однакові висоти, то відношення їх площ дорівнює відношенню довжин основ.

Задача 3. Якщо вершину трикутника пересувати по прямій, паралельній основі, то площа трикутника при цьому не зміниться.

(висота і основа трикутників залишаться не змінними, тоді і площа не зміниться).

Задача 4. Площі трикутників, що мають спільний кут, пропорційні добуткам сторін, що утворюють цей кут:

=

Доведення: 1) Проведемо відрізок ВС_1.

2) =(відношення площ трикутників з

рівними висотами, задача 2).

 =

3) Перемножимо останні дві рівності, отримаємо:=.

Висновок: Якщо два трикутника мають спільний кут, то їх площі відносяться як добутки сторін, що укладають цей кут.

Задача 5. Медіана трикутника ділить його на дві рівновеликі частини.

Доведення.

                  

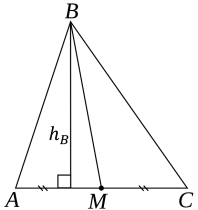
     S_ABМ =AМ·h_B,

     S_BМС =МС·h_B, за умовою МС=АМ,

              тоді  S_ABМ=S_{BМС .}

 

Задача 6. (Про площі суміжних трикутників). Якщо пряма, проведена з вершини трикутника, ділить протилежну сторону у відношенні m : n, то і площу трикутника вона ділить в такому ж відношенні.

                         Доведення.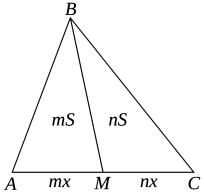 

            S_ABМ =AМ·h_B= mx·h_B,

            S_BМС =МС·h_B = nx·h_B,

                      тоді   ==.

Задача 7.  У трикутнику точку перетину медіан з'єднали з вершинами трикутника, тоді площа кожного з отриманих трикутників становить третю частина площі даного трикутника (довести).

 Доведення.

За задачею 5 маємо, що

  S_AOB = S_BOC = S_AOC =  S_ABC.

Задача 8. Медіани трикутника ділять його на 6 рівновеликих частин.

              Доведення.

1) Нехай точка О — точка перетину медіан AK, BL и CM трикутника  ∆ABC.

2) ОМ, ОК, ОL — медіани ∆AОB,  ∆BОC, ∆AОС.

3)  Тоді S_AOМ = S_BOМ=x_,

                        S_КOB = S_КOC=y_,   

               S_AOL = S_COL= z

S_BLC=  S_ABL = y+y+z=x+x+z, тоді х = у

 S_AСК = S_BАК = х+х+у=z+z+y, тоді х = z, отже і y = z.

Висновок: x = y = z, тобто медіани трикутника ділять його на 6 рівновеликих трикутників.

Задача 9. Якщо пряма, проведена з вершини трикутника, ділить

протилежну сторону у відношенні m:n, тоді для будь-якої точки К, що належить цій прямій, =.                Доведення:   =, (задача 5).

 

 

 

 

 

 

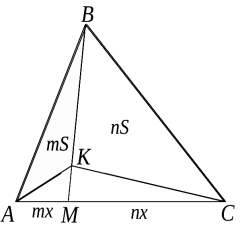
З 1) і 2) маємо, що  =.

Задача 10. Відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності.

        Доведення:

     ΔАВС~ΔА₁В₁С₁,

k — коефіцієнт подібності, ∠А=∠А_1, ∠В=∠В_1,∠С=∠С_1,

за  задачею 4, == k²,  (площі трикутників, мають спільний кут,

пропорційні добуткам сторін, що утворюють цей кут).

      Дане твердження справедливо і для подібних многокутників, так як їх

можна розбити на відповідні подібні трикутники.

Задача 11. Середня лінія трикутника, що має площу S, відсікає від нього

трикутник, площа якого дорівнює S.

  Доведення:  Площа ΔАВС дорівнює S,  МN — середня лінія.  ΔАВС~ΔМСN, тоді = k² = 4, тоді k = 2.

    S_MCN = =S.                                                               

Задача 12. Середні лінії трикутника поділяють його на чотири рівновеликих трикутника.

               S_AML = S_MBK=S_KCL = S_MKL

 

1.2. Пропорційність і площа паралелограма

Задача 13. На стороні AD взята точка M. S_ВMС =S_. Довести, що S_AВСD =2S.

                                                                                            Доведення:

   1. Проведемо через точку M пряму, паралельну стороні AB.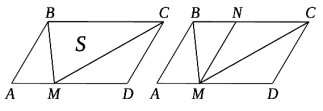

2. ΔABM = ΔNMB, тоді   S_AВМ = S_NMB.

3. ∆MNC = ∆MCD,  тоді   S_MNC = S_MCD.

4. S_MCD= S_,  S_AВCD=2 S_ВМN + 2 S_МNC=2( S_ВМN + S_МNC) =  2 S_ВМC=2S. S_AВCD=2S.

Задача 14. Точка M взята всередині паралелограма і з'єднана з усіма його вершинами. Площа заштрихованої частини паралелограма дорівнює S. Довести, що площа паралелограма дорівнює 2S.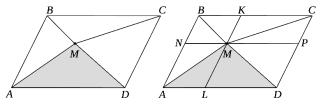

   Доведення:  1). Проведемо через точку М прямі паралельні сторонам паралелограма.

2). NBKM − паралелограм, тоді S_∆NBM = S _∆BKM; KMPC − паралелограм, тоді

S_∆CMP = S_∆CMK; LMPD − паралелограм, тоді S_∆LMD = S_∆DMP; ANML − паралелограм, тоді ∆ABC   3). S_{зафарбованої частини}= S, тоді площа  S_АВСD=2S.

Задача 15. ABCD − паралелограм. O – довільна точка. Довести:

S_∆OCD = S ₁ + S ₃ − S ₂ .                                                     Доведення:

 

 

 

 

 

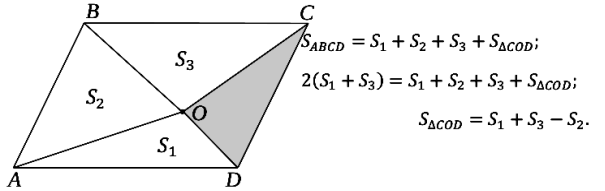
Задача 16. ABCD — паралелограм, AK = DE.

Довести, що S_АВСD = S ₁ + S ₂ + S ₃+ S ₄

Задача 17. Діагоналі паралелограма ділять його на чотири рівновеликі частини.

Доведення: Точка O - точка перетину діагоналей.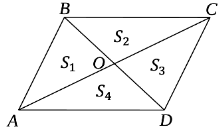

1) ∆ABC = ∆ACD за трьома сторонами, тоді площі цих трикутників рівні. 2) ВО -медіана ∆ABC, тоді за задачею 5,  S_∆АОВ = S_∆BОС,  S₁= S₂.  3) Аналогічно S₃ = S₄. 4) Тому що ∆ABC = ∆ACD, маємо що S₁= S₂ =S₃ = S₄.

1.3  Пропорційність і подібність в трапеції

Задача 18. (Властивість трикутників, на які розбивається

трапеція її діагоналями) Діагоналі трапеції розбивають її на 4 трикутника, причому трикутники, прилеглі до основ, подібні, а трикутники,

прилеглі до бічних сторонах, рівновеликі.

Доведення: 1) ΔBOC ~ ΔAOD за двома кутами (I ознака подібності).

2) Трикутники ВОС і COD мають спільну висоту СН, якщо прийняти за їх основи

відрізки ОВ і ОD.

3)   ===k, тоді   S_COD =S_BOC.

4) Трикутники ВОС і АОВ мають спільну висоту ВР, якщо  прийняти за їх основи відрізки СО і ОА, тоді аналогічно до попереднього отримаємо

 S_АОВ =S_BOC. Тоді   S_COD  =  S_АОВ.

Задача 19. (Зв'язок між площами трикутників, на які розбивається трапеція її діагоналями) О-точка перетину діагоналей трапеції ABCD з основами BC і AD, тоді S_ABCD = (+ )² .

Доведення:  ΔBOC ~ ΔAOD, тоді = = k², =k (задача 18),

тоді  k =,   S_COD =S_BOC = ·S₁ =.

S_ABCD = S_BOC + 2S_COD +  S_АОD.

S_ABCD=  S₁   +  S₂ + 2= (+ )² .

Задача 20.

1.4  Пропорційність при обчисленні площ довільних многокутників

       Бімедіани чотирикутника - це відрізки, що з'єднують середини

протилежних сторін. Одна з основних теорем про бімедіанах і площі фігур належить французькому механіку і інженеру П'єру Варіньону (1654-1722), який написав підручник з елементарної геометрії, в якому ця теорема вперше і з'явилася.

Теорема Варіньона. Чотирикутник, утворений шляхом послідовного з'єднання середин сторін опуклого чотирикутника, є паралелограмом і його площа дорівнює половині площі даного чотирикутника. S_MNPK =S_ADCD.

Наслідки з теореми: 1). Паралелограм Варіньона є

ромбом, якщо в початковому чотирикутнику

діагоналі рівні і бімедіани перпендикулярні.

2). Паралелограм Варіньона є прямокутником, якщо у вихідному чотирикутнику діагоналі перпендикулярні

і бімедіани рівні. 3). Паралелограм Варіньона є квадратом, якщо в початковому чотирикутнику діагоналі рівні і перпендикулярні, бімедіани рівні і перпендикулярні.

Задача 21. Суми площ навхрест розміщених чотирикутників, утворених перетином бімедіан опуклого чотирикутника рівні.

1. S _MBN + S _KPD = S _ABC + S _ACD = S _ABCD = S _BCD+

+ S_ABD=S _NCP + S _AMK .

2. MNPK — паралелограм, діагоналі ділять його на чотири рівновеликих трикутника,

S_MNO = S_NOP = S_KOP = S_MOK .

3.  (S _MBN +S_MNO)+( S_KPD+S_KOP ) = (S_NCP+ S_NOP)+ (S_AMK + S_MOK).

S_MBNO + S_KOPD =  S_NCPO +  S_AMOK.

Задача 22. S _ABCD = 2S _EBFD ⇔ S _EBFD = S_{ABCD .}

Доведення: 1. Зʼднаємо точки В і D.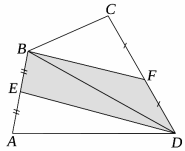

2. ∆ABD, DE − медіана, тоді S _EBD = S_АBD (медіана ділить трикутник на два рівновеликих).

3. ∆CBD, BF − медіана, тоді  S _BFD =   S _BCD.

S _EBD +  S _BFD =  S_АBD +  S _{BCD ,}  тоді S _EBFD = S_{ABCD .}

Задача 23. Нехай O - точка перетину діагоналей чотирикутника ABCD,  довести рівність = .

Доведення: 1) Площі трикутників, що мають одну й ту ж саму основу, пропорційні висотам, тоді

= .   

2) ∆AOM ∾ ∆CON (за двома кутами), тоді

 =. Отже  = .

Задача 24. Діагоналі розбивають опуклий чотирикутник на

трикутники з площами S₁, S₂, S₃ і S₄ (S₁ і S ₃ - площі трикутників,

прилеглих до протилежних сторонах чотирикутника). Довести, що

S₁ ∙ S₃ = S₂ ∙ S₄ .

Доведення: О — точка перетину діагоналей.

= , тоді =

=  , тоді =

= , звідси S₁ ∙ S₃ = S₂ ∙ S₄ .

Висновок: Результатом розв'язання розглянутих опорних задач стали формули,

які застосовуються при розв'язанні складних геометричних задач. (див.додаток)

 

2 РОЗВʼЯЗАННЯ ЗАДАЧ З ВИКОРИСТАННЯМ ВЛАСТИВОСТЕЙ ПЛОЩ

2.1  Бісектриса, медіана, висота трикутника і відношення площ

Задача 1. У трикутнику ABC сторони AB = 4 см, BC = 5 см, BD — бісектриса. Знайти відношення площі трикутника ABD і площі трикутника ABC.

Розвʼязання: = = = . Якщо позначити

S_ABD = 4х, S_DBC = 5x, S_ABC = 9x, тоді = .

 

Задача 2. Медіана BM і бісектриса AP трикутника ABC перетинаються в

точці K, довжина сторони AC втричі більше довжини сторони AB. Знайти відношення площі чотирикутника KPCM до площі трикутника ABC.

Розвʼязання.  Позначемо S _ABC = S.

1. BM — медіана, тоді S_ABM = S_MBC = 0,5 ∙ S (медіана

трикутника ділить його на два рівновеликих трикутника).

2. AP – бисектриса, тоді BP : PC = AB: AC = 1: 3 (властивість бісектриси трикутника).

3. S _BAP : S _PAC = 1: 3 (відношення площ трикутників з рівними висотами).

4. S _ABC = S = 4 ∙ S_BAP , тоді S_BAP = S, отже S_PAC = S.

5. ΔАВМ, АК-бісектриса, АМ== = 1,5АВ; = =.

6. S_ABM = S_AMK + S_ABK,   S_ABK : S_AMK = 2:3

  S_ABM = 0,5S,  S_ABK = 0,5S: 5 ∙ 3 = 0,3S,   S_ABK = 0,5S: 5 ∙ 2 = 0,2S.

7. S _MCPK = S _ACP − S _AMK = S — 0,3S =0,45S.

8. = = 0,45 =.   Відповідь: .

Задача 3. Рівнобедрений трикутник розділили бисектрисою кута при

основі на два трикутника: площа першого (прилеглого до основи) 6, площа другого 5. Знайти сторони трикутника.

Розвʼязання:  1) S _ABC =  6 + 5 = 12, = =

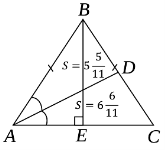
(задача про відношення площ трикутників, що мають рівні кути). 2)  = (властивість бісектриси кутів трикутника), тоді = = 5 : 6 =, тоді = . 

3) Проведемо висоту BE⟘AC. Позначимо AB = 5x, AC = 6x, то ЕС = AE = 3x, за теоремою Піфагора  BE = 4x. 4) S_ABC = AC ∙ BE = 6х ∙ 4х =12х², але  S_ABC = 12,

тоді х = 1, отже АВ = 5, АС = 6, ВС = 5.

Відповідь: АВ = 5, АС = 6, ВС = 5.

Задача 4. У рівнобедреному ΔABC бічні сторони BC і AC в два рази більше

основи AB. Бісектриси кутів при основі перетинаються в точці M. Яку

частина ΔABC становить площа ΔAMB?

Розвʼязання:  1) Позначимо S _ABC = 1.  ΔABC, АА₁ — бісектриса, = = ,  = ,  S _ABА1,  ВМ — бісектриса, = = = = , 

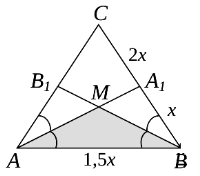
S _ABМ = S _AА1В = · = . Відповідь: .

Задача 5. У ΔABC відомо, що AB = 6, BC = 9, AC = 10. Бісектриса кута B

перетинає сторону AC в точці M. На відрізку BM взята точка O так, що

BO: OM = 3: 1. Площа якого з трикутників AOB, BOC або AOC є найменшою?

Розв'язання: 1. ΔABC; BM — бісектриса, тоді

                                                  Тоді найменшу площу має трикутник АОС.

Задача 6. У ΔABC проведені бісектриси BD і AE. Знайти відношення площ

трикутників ABC і BDE, якщо AB = 5, BC = 8, AC = 7.

Розв'язання: 1. ΔABC; BD — бісектриса.

Відповідь: .

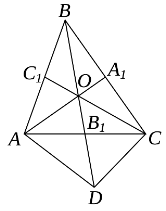
Задача 7. Медіани трикутника 3, 4 и 5. Знайти площу трикутника.

Розв'язання: 1. Нехай AA₁ = 3, BB₁ = 4, CC₁ = 5, тоді АО=2, СО=, В₁О=.          2. S_АBC = 3S_AOC.                                                                                                               3. Доповнимо трикутник АОС до паралелограма АОСD (В₁О= В₁D).

4. S_AOD = AO · AD sinA = ·2 · sinA =  sinA.

5. За теоремою косинусів OD²= AO² + AD² — 2 AO · AD · cosA

 

 

 

 

 

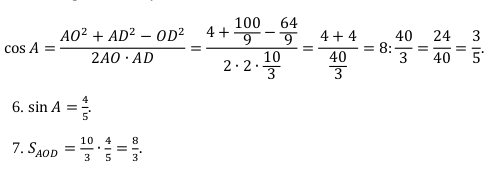
8. S _ABC = 3S _AOC = 3S _AOD = 3 ∙ = 8.         Відповідь: 8.

Висновок: При розв'язанні задач були використані: властивість бісектриси кута трикутника; властивість медіан; відношення площ трикутників, що мають рівний кут; відношення площ трикутників із спільною основою або спільною

висотою.

2.2 Відношення площ подібних трикутників

Задача 8. У середині трикутника ABC взята точка M, через яку проведені

прямі, паралельні сторонам трикутника. При цьому площі трьох утворених трикутників з вершиною M рівні S₁, S₂, S₃. знайти площу трикутника ABC.

Розв'язання: Так як ΔABC ~ ΔA₁A₂M, ΔABC ~ ΔB₁B₂M, ΔABC ~ ΔC₁C₂M, то їх

площі відносяться як квадрати відповідних елементів. Нехай S_ABC = S, AC₂ = a, C₁C₂ = b, C₁C = c.

 

 

 

 

 

 

Задача 9. Пряма, паралельна основі трикутника, ділить його на частини,

площі яких відносяться як 2:1, рахуючи від вершини. В якому відношенні

вона ділить бічні сторони?

Розвʼязання: ∆MBN~∆ABC,  = . Нехай BN = x, NC = y. Тоді (х : (х+у))² =,  3х²= 2(х² + 2ху+ у²),  х² — 4ху — 2у² = 0, поділемо на у², і введемо заміну = t, t² — 4t — 2 = 0,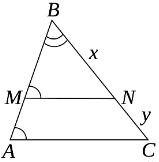 

t_1,2 = 2 ±,  t > 0, = 2 +.

Відповідь: у відношенні (2 +) : 1.

Задача 10. На сторонах AB, BC і CA взяті точки K, M і P так, що

AK: AB = BM: BC = CP: CA = 1: 3. Довести, що площа трикутника, обмеженого прямими АМ, ВР і СК, складає площі трикутника АВС.

Розвʼязання.    1. Нехай S_АBC = S.   

  = , тоді S_АBМ = S (задача про відношення площ з рівними висотами).  S_ВРС = S,  S_АКС = S.

2. Проведемо MM₁║CK. За теоремою Фалеса:

 

 

 

 

 

 

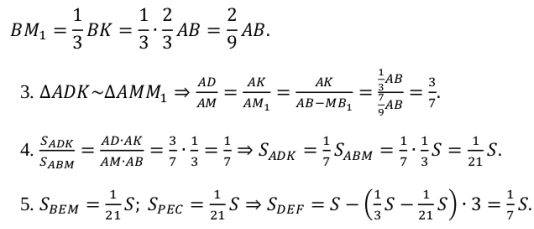
Висновок: при розв'язанні задач використовувалися наступні опорні задачі:

1) Площі подібних многокутників відносяться як квадрати відповідніх

сторін. 2) Площі двох трикутників, що мають рівні кути, відносяться, як

добутки сторін, что утворюють ці кути. 3) Теорема Фалеса. 4) Відношення площ трикутників з рівними висотами дорівнює відношенню їх основ.

2.3 Пропорціональность і площа трапеції

Задача 11. Довжини основ трапеції дорівнюють 2 і 5. Площа трикутника,

прилеглого до однієї з бічних сторін дорівнює 10. Знайдіть площу всієї трапеції.

Розвʼязання. За властивістю площ трикутників маємо

S₂S₄ =S₁ S₃ , тоді  S₁S₃ =100

S₁ =  S₃ ,  S₁ S₃ = S₃² = 100,

S₃ = 10: = 25, тоді S₁ = 4, а S _ABCD = 10 + 10 + 4 + 25 = 49

Відповідь: 49.

Задача 12. Точка М що лежить на стороні паралелограма ABCD, з'єднана

з вершиною В. Діагональ АС перетинає відрізок ВМ в точці К.

Площа ΔКВС дорівнює 6, площа ΔКМС дорівнює 4. Знайти площу паралелограма АВСD.

Розвʼязання.

1) АВСМ – трапеція. За властивістю площ:

S ₁ S ₃ = S ₂ S ₄;  S₁ = S₃ = 6; 4S ₂ =36, S ₂ =9, то

S _ABC =S _ADC =15; S _ABCD =15+15=30.

Відповідь: 30.

2.4 Площа многокутника

Задача 13. Дано  чотирикутник ABCD. Середини сторін AB і CD - точки K і M, точка перетину відрізків BM і CK -  точка P, точка перетину відрізків AM і DK -  точка O. Доведіть, що S _MOKP =S _BPC + S _AOD.

Розвʼязання: Проведемо діагональ ВD,

DK – медіана ∆ADB, тоді S_ADK = S_ABD .

BM – медіана ∆DBC, тоді S_BMC = S_BCD.

S_ADK + S_BMC = S_ABD + S_BCD = S_ABCD.

AM – медіана ∆ADC, тоді S_AMK = S_ADC.

KC – медіана ∆ACB, тоді S_BKC = S_ABC.

S_AMD + S_BKC = S_ADC + S_ABC = S_ABCD.

S_ADK + S_BMC + S_AMD + S_BKC = S_ABCD.

8. (S_AKO + S_AOD) + (S_BPC + S_MPC ) + (S_AOD + S_MOD) + (S_BPC + S_BKP) = S_OKPM +

S_BPC + S_MPC + S_AOD + S_MOD + S_AKO + S_BKP, отже S_OKPM = S_BPC + S_AOD.

Задача 14. Площа чотирикутника ABCD дорівнює 1. На сторонах

AB, BC, CD і DA взяті точки K, M, P і L відповідно. Відомо, що K -

середина AB, BM: MC = 1: 5, CP: PD = 2: 1, DL: LA = 1: 3. Знайдіть площу

шестикутника AKMCPL.

Розвʼязання:

 

 

 

Відповідь: S _AKMCPL = .

 

 

 

 

 

 

 

 

ВИСНОВКИ

      Вивчення математики відбувається в процесі розвʼязання задач, знання особливих прийомів і підходів до розвʼязання задач, дозволяють вирішувати їх правильно, просто і оригінально. Опорні задачі склали основу для розвʼязання інших, більш складних задач.

      В ході роботи розібрано та розвязана велика кількість задач різного рівня складності. Це дозволило осмислити і створити цілісне уявлення про пропорційності при обчисленні площ многокутників, засвоїти на практиці набуті знання.

     Таким чином, мета роботи досягнута.

Практична значимість: знання прийомів і підходів до розвʼязання задач на відношення пропорційності площ фігур дозволяє успішно розвʼязувати складні,

конкурсні та олімпіадні задачі на відношення; можливість використання матеріалів дослідження для гурткової та позакласної роботи.

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Підручник Геометрія 8 клас Істер, Видавництво: Генеза, Київ 2016, 213

2. Підручник Геометрія 8 клас, Мерзляк А.Г., Полонський В.Б., Якір М.С.
Видавництво: Гімназія, Харків, 2016, 208.

3. Підручник Геометрія 9 клас, (авт. Бурда М.І., Тарасенкова Н.А.), Видавництво: Оріон, 2017, 224
4. http://genius.pstu.ru/mod/resource/view.php?id=36

5. https://prezi.com/zzedvfgpvqsk/presentation/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток

Опорні задачі «Пропорційність при обчисленні площ многокутників»