Простора система сил. Поняття про момент сили відносно осі. Центр паралельних сил. Центр ваги тіла. Визначення центра ваги плоских фігур

Лекція з дисципліни

«Технічна механіка»

273 Залізничний транспорт

Галузь знань 27 «Транспорт»

освітньо-кваліфікаційний  рівень молодший спеціаліст

для студентів заочної форми навчання

Лекція № 2

Дисципліна: Технічна механіка

Блок МПН.08.01 Види напруженого стану деталей

Модуль ПФ.С.ОЗ.Р.03.10-1 Види напруженого стану деталей

Тема:  Простора система сил. Поняття про момент сили відносно осі.

Центр паралельних сил. Центр ваги тіла. Визначення центра ваги плоских фігур.

План  лекції:

1. Плоская система произвольно расположенных сил и условие ее равновесия

2. Рівновага просторової системи сил.

3. Момент сили відносно осі

4. Центр ваги

Плоская система произвольно расположенных сил и условие ее равновесия

       Приведення сили до цієї точки полягає в тому, що розглядається силу F переносять паралельно самій собі в довільно обрану точку О. Для того щоб механічний стан тіла не змінилося, силу F врівноважують силою F "(рисунок 1).

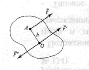
Рисунок 1-Плоска система

          В результаті приведення сили F до точки Про вийшла система сил, що складається з сили F /, рівній і паралельної даній силі F, і пари сил (F і F "), момент якої дорівнює моменту цієї сили F щодо точки 0.

М = M0(F).

Рівновага просторової системи сил.

           Будь-яку силу P можна представити діагоналлю прямокутного паралелепіпеда, побудованого на складових X, Y Z, які по модулю рівні проекція даної сили на осі координат х, у, z. Модуль і напрям P визначав за формулами:

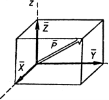
P  ,



cos(P,

24.  X ,

P



cos(P,

25.  Y ,

P



cos(P,

26.  Z .

P

Рисунок 2-Прямокутний параллелепипед

          Система сил, лінії дії яких не лежать в одній площині, але. перетинаються даній точці, називається просторової системою сходяться сил. Рівнодіюча просторової системи  сил, що сходяться,  дорівнює геометричній сумі доданків сил:

R  P1  P 2  ...  P n  ∑ P .

      Рівнодіюча R виражається замикає стороною просторового силового багатокутника, сторони якого рівні й паралельні даним силам. Зокрема, якщо число доданків сходяться сил дорівнює трьом, то їх рівнодіюча по модулю і напрямку виражається діагоналлю паралелепіпеда, побудованого на цих силах. Силовий багатокутник просторових жавної системи сходяться сил не є плоскою фігурою, тому при додаванні сходяться сил, які не лежать в одній площині, краще аналітичний метод.

Теорема. Проекція рівнодіюча системи сходяться сил на ка- кую-небудь вісь дорівнює сумі проекцій всіх сил на цю ж вісь.

Rx  ∑ X ,

      
                                
RY  ∑Y ,   
Rz  ∑ Z .

Рівновага просторової системи збіжних сил

             Для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб рівнодіюча цієї системи сил дорівнювала нулю, т.е.

P = ∑ P = 0

         Ця  рівність висловлює умова замкнутості силового багатокутника

даної системи сил, т. е. умова рівноваги просторової системи  сил, що сходяться, в геометричній формі. Замість векторної рівності можна зіставити три скалярних:

∑ X  0 , ∑Y  0 , ∑ Z  0 ,

які виражають умови рівноваги просторової системи збіжних сил в аналітичній формі і їх називають рівняннями рівноваги просторової системи збіжних сил. Система рівнянь дозволяє визначити тільки три невідомих. Якщо число невідомих більше трьох, то пространст- венная система сходяться сил є статично невизначеної.

Момент сили відносно осі

     Момент сили Р відносно осі z дорівнює моменту проекції цієї сили на площину, перпендикулярну до осі z, щодо точки О (точка пересічення осі z площиною τ)

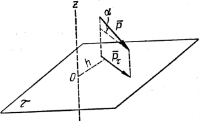
M z (P)  M o ( P ),

M P  P h  Ph cos ,

o  

Рисунок 3- Момент сили відносно осі

де Р τ  - проекція сили P на площину τ, перпендикулярні до осі z; h - довжина перпендикуляра, спущеного з точки О на лінію дії проекції P τ

Відзначимо, що проекція сили на вісь - скалярна величина; проекція сили на площину - вектор.

Момент вважається позитивним, якщо, дивлячись з кінця позитивного напрямку осі,  бачимо обертання площини  під дією складової P против часовой стрелки.

В іншому випадку момент вважається негативним. Момент сили відносно осі дорівнює нулю, якщо сила перетинає вісь (h = 0)

або паралельна осі( P = 0 ).

Рівновага довільної просторової системи сил

Теорема. Для рівноваги просторової системи сил необхідно і достатньо, щоб головний вектор і головний момент дорівнювали нулю, т. е.

R  0 , М   0 .

Ці два векторних рівності можна замінити шістьма скалярними:

∑ Х  0 ; ∑Y  0 ; ∑ Z  0 ;

∑ М х=0; ∑ М Y=0; ∑ М Z=0

Наведені умови називають рівняннями рівноваги довільної просторової системи сил: для рівноваги тіла в просторі необхідно і досить, щоб суми проекцій всіх сил на координатні осі і суми моментів всіх сил щодо трьох координатних осей дорівнювали нулю.

Центри ваги

Сила тяжіння - це сила, з якою тіло притягується до землі. Центр тяжкості - це точка прикладання сили тяжіння (рисунок 4).

Рисунок 4-Центр тяжкості

Положення центра ваги простих геометричних фігур: 1) в прямокутнику, квадраті, ромбі, параллелограмме - на перетині діагоналей (рисунок 5);

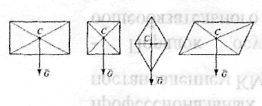
Рисунок 5-Геометричні фігури

1) в трикутнику - на перетині медіан (рисунок 6):

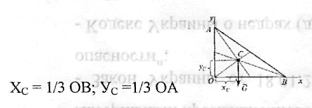
Рисунок 6-Трикутник

2) в круговому секторі або півколі - в точці з координатами:.

а)Хс = г,   Ус=2г/3я  (рисунок 7,а) б)Хс = 2г/Зл:  Ус = г (рисунок 7,6)

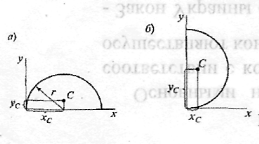
Рисунок 7-Кути

3) в конусі або повної піраміді - на 1/3 висоти від підстави (рисунок 8):

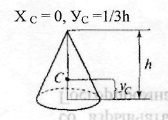
Рисунок 8-Конус

Якщо плоска фігура має неправильну геометричну форму, то центр ваги такої фігури можна визначити двома способами:

1) методом підвішування фігури на вістрі;

2) теоретичним методом. В цьому випадку плоска фігура розбивається на певну кількість елементарних фігур, що мають правильну геометричну форму. Потім визначається положення центра ваги і площі кожної елементарної фігури. Для того щоб знайти координати центру ваги заданої складної фігури, використовуються наступні формули:

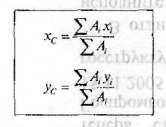
де :

А і - площі елементарних фігур, на які розбита складна фігура;

хі, уі; - координати центру ваги кожної елементарної фігури щодо випадкових осей        х і у.

Контрольні питання:

1 Дати пояснення плоскої системи произвольно расположенных сил и условие ее равновесия

2 Дати визначення  рівноваги просторової системи сил.

3 Дати пояснення моменту сили відносно осі

4 Що називається центром ваги ?

Література:

1М.С. Мовнин, А.Б. Йзраелит, А.Г. Рубашкін «Основи технічної механіки», с 26-54