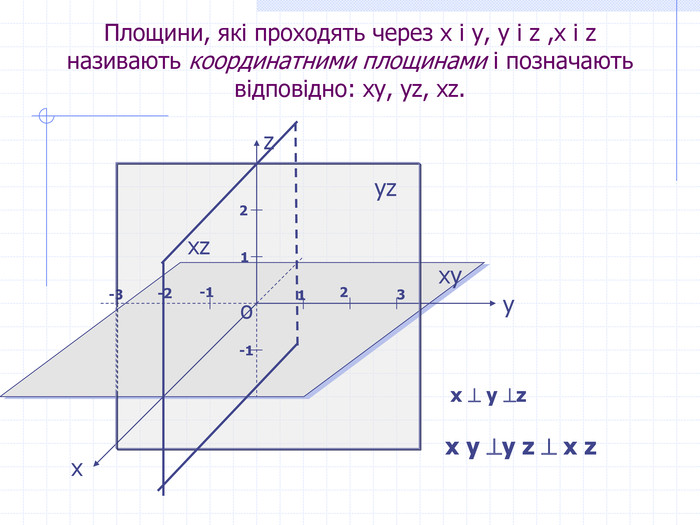
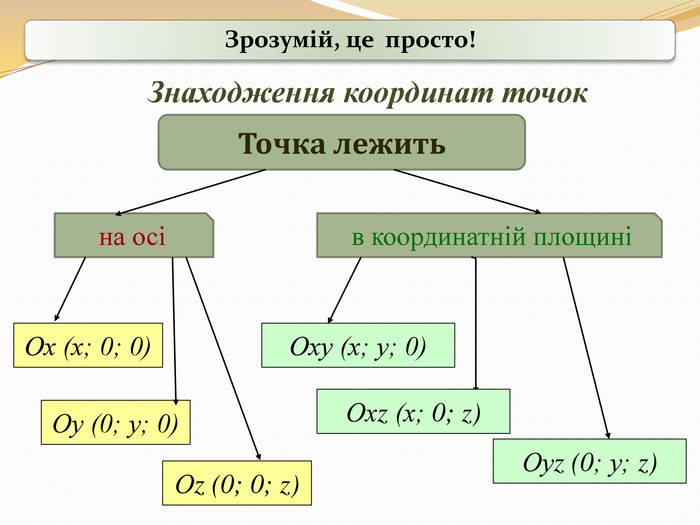
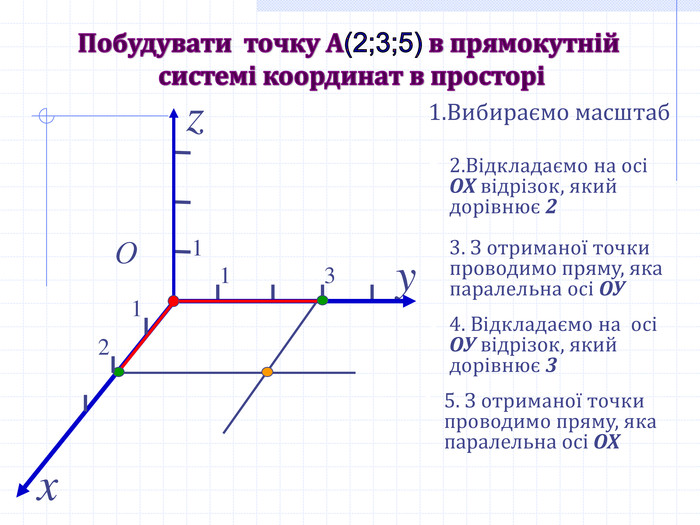
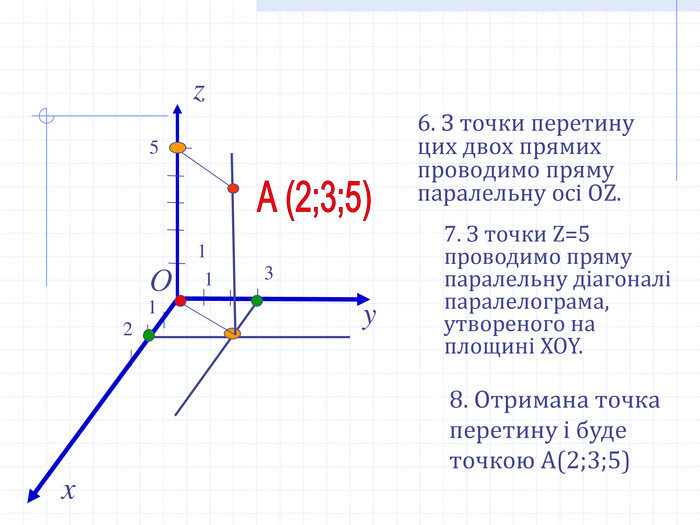
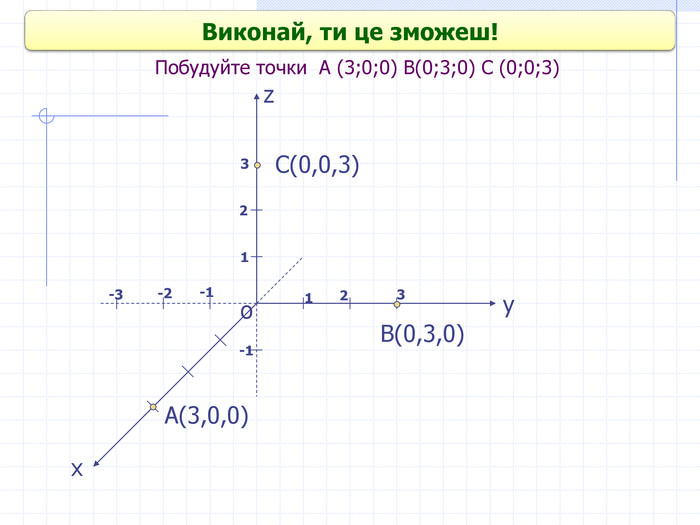
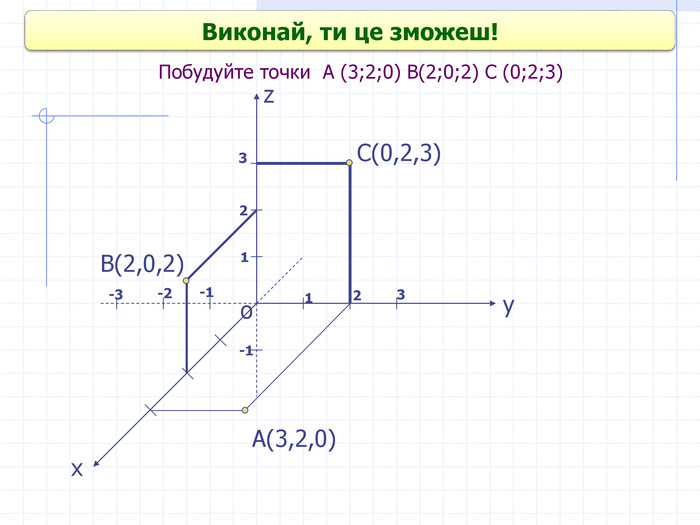
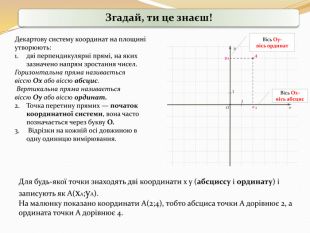
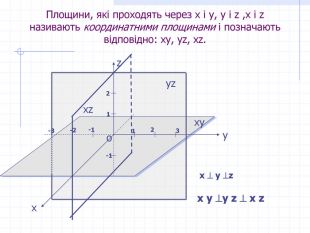
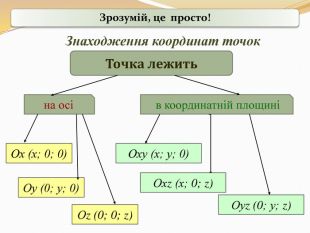
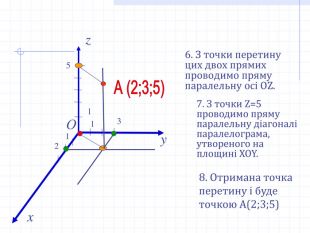
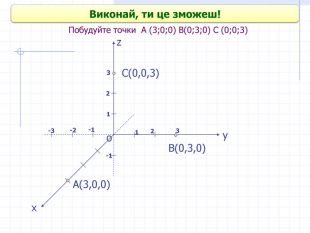
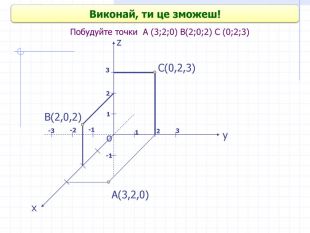
Прямокутні декартові координати у просторі
Про матеріал
Презентація до уроку геометрії в 10 класі "Прямокутні координати у просторі" Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку