Тест "Піраміда. Правильна піраміда"

Тестові завдання «Піраміда»

1.          (0.5б) Пірамідою називають многогранник, у якого одна з граней - …., а інші грані … зі спільною вершиною

А) трикутник, трикутники;   Б) довільний трикутник, квадрати; В) довільний чотирикутник, паралелограми  Г) довільний многокутник; трикутники

2.(0.5 б) Піраміда називається правильною, якщо

А)в неї всі бічні ребра рівні; Б) її основою є правильний многокутник, центр якого збігається з основою висоти піраміди;  В) в основі лежить правильний многокутник Г) якщо всі її бічні грані - правильні трикутники

3.(0.5 б) Апофемою називають

А) висоту піраміди; Б) висоту піраміди проведену з її вершини; В) висоту бічної  грані; Г) висоту бічної грані правильної піраміди, проведеної з її вершини

4. (0.5 б) Відрізок, що сполучає вер­шину піраміди з вершиною основи, називається..

А) бічним ребром  Б) висотою  А) апофемою   Г) діагоналлю

5. (1 б)

6. (1б)Знайти площу бічної поверхні правильної шестикутної піраміди, якщо апофема 10 см, а сторона основи – 6 см.

А) 180 см²;  Б) 360 см²;  В) 240 см²; Г) 160 см²; Д) 560 см²7.

7. (1б)Бічна поверхня правильної трикутної призми дорівнює 96 см². Сторона основи – 8 см. Чому дорівнює апофема?

А) 3 см;  Б) 4 см;   В) 6 см;  Г) 7 см; Д) 8 см

8. (1б)В основі трикутної піраміди лежить прямокутний трикутник з катетами 6 і 8 см. Усі бічні грані мають площу 10 см². Чому дорівнює площа  повної поверхні?

А)48 см²;  Б) 54 см²;  В) 78 см²;  Г) 88 см²  Д) 480 см²

9. (1б)Апофема правильної чотирикутної піраміди дорівнює 5 см, сторона основи – 8 см. Знайдіть площу повної поверхні піраміди.

А) 80 см²;  Б) 144 см² ;  В) 224 см² ;   Г)  76√3 см² ;  Д) 60+16√3 см²

10 (1б)

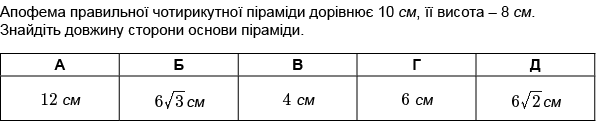
11 (1б)

12 (1б)

13. (1б) Апофема правильної трикутної піраміди дорівнює 6 см, а радіус кола, вписаного в її основу дорівнює √3 см. Обчисліть бічну поверхню піраміди.

 А) 36 см² ;  Б)     54 см²    В) 109 см²;     Г)  72 см²  Д)  108 см²

14. (1б)Апофема правильної трикутної піраміди дорівнює 8 см, а радіус кола, описаного навколо основи дорівнює 2√3 см. Обчисліть бічну поверхню піраміди.

 А) 36 см² ;  Б)     37 см²    В) 48√3 см²;     Г)  72 см²  Д)  144 см²