"Прямокутні координати в просторі"

План-конспект заняття

Навчальна дисципліна: Математика

Тема заняття: Прямокутні координати в просторі.

Мета заняття: сформувати уявлення про декартову прямокутну систему координат у просторі; ознайомити з формулами для знаходження відстані між двома точками в просторі та знаходження середини відрізка; сформувати вміння застосовувати ці формули до розв’язування задач; розвивати просторову уяву, вміння проводити аналогії, порівняння; виховувати акуратність, зацікавленість у пізнанні нового.

Тип заняття: комбіноване заняття

Міжпредметні зв’язки: історія математики, архітектура

Забезпечення заняття

Матеріально-технічне забезпечення та дидактичні засоби, ТНЗ             моделі фігур__________________________________________________

Література:

1. Основна
2. Додаткова

План заняття

І. Підготовчий етап

Викладач перевіряє готовність студентів до заняття, відмічає відсутніх.

Перевірка домашнього завдання.

   Перевірити наявність домашніх завдань в зошитах і відповісти на запитання, які  виникли в процесі їх виконання

В свій час Рене Декарт сказав: «… нащадки будуть вдячні мені не тільки за те, що я сказав, але і за те, що я не сказав і тим самим дав їм можливість і задоволення додуматися до цього самостійно…» Сьогодні на уроці ми будемо знайомитися з декартовою системою координат разом. Хто ж такий Рене Декарт? 

  Французький вчений ХVI  століття Рене Декарт в своїй праці   «Геометрія» писав: «Уяви собі місто, яке  сплановано на американський  манер,в якому проспекти йдуть на південь і на  північ, а вулиці на схід і захід. Якщо вибрати деякий проспект і деяку вулицю як початкові, а їх перетин як початок  відліку, від якого послідовно відлічуються  номери проспектів та вулиць, то ці  номери дають адресу,по якій уявляємо відповідне місто. Така ідея дозволяє нам одночасно визначити положення будь якої точки на площині».                        

   «Геометрія» Декарта вийшла в світ у 1637 році. Це міцний  пам’ятник його слави. З її появою почалася нова ера в розвитку математики. Декарт, застосуванням декартової системи, встановив зв’язок між алгеброю і геометрією і був основоположником аналітичної геометрії.

ІІ. Основний етап

Мотивація навчальної діяльності

Одного дня польський письменник Станіслав Лен сказав, що для того, щоб щось  пізнати, треба вже щось знати. Давайте згадаємо, що ми вже знаємо про декартову систему координат. Суть координат або система координат полягає в тому, що це правило, по якому визначається положення об’єкту. Система координат оточує нас всюди:

- спілкуючись один з одним люди часто говорять: «Залиште свої координати». Для чого?  Для того, щоб людину було легко знайти.

Це може бути: номер телефону, домашня адреса, місце роботи, електрона адреса. Де ще людина зустрічається з координатами:

 Відповіді:

а) місце в кінотеатрі;

б) система географічних координат (широта, довгота);

в) гра «Морський бій»

г) льотчики, моряки за допомогою координат визначають положення об’єкту;

д) туристичні схеми;

є) при астрономічних спостереженнях.

Актуалiзацiя опорних знань

Ви вже вивчали  декартову систему координат на прямій і на площині. А сьогодні ми познайомимось з декартовою системою координат в просторі, будемо навчатися знаходити координати точок, зображених в декартовій системі  координат, будувати точки за заданими координатами.

Бесіда

При вивченні теми «Координатна пряма» ви навчилися знаходити по координаті положення точки на прямій.

• Так скільки ж координат треба для того, щоб задати точку на прямій?

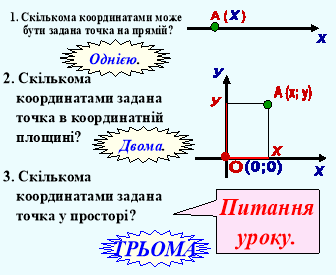
  Зараз повторимо і пригадаємо всі терміни і поняття, які асоціюються у вас з цими словами - прямокутна система координат

Сприйняття й усвідомлення нового матеріалу

Лекція

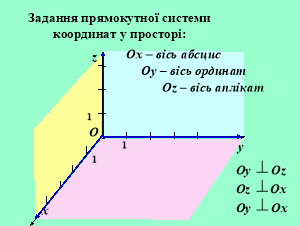Розглянемо три взаємно перпендикулярні прямі (координатні осі) Ox, Oy, Oz зі спільною точкою O — початком координат. Ox — вісь абсцис; Oy — вісь ординат, Oz — вісь аплікат. Через кожну пару цих прямих проведемо координатні площини Oxy, Oxz, Oyz. Утворену в такий спосіб систему координат називають прямокутною декартовою системою координат у просторі.

Кожній точці в просторі відповідають три числа: її абсциса Х, ордината Y, апліката Z. І навпаки: кожній точці чисел (х,y,z) у просторі відповідає єдина точка. Координати точки записується у дужках через крапку з комою, причому першою записується Х, другою У, третьою Z.

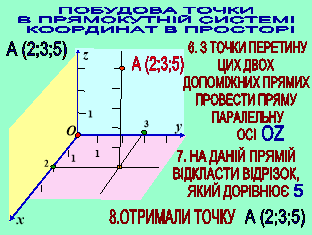
Складання алгоритму побудови точки

  Давайте разом з вами складемо алгоритм побудови точки А (2;3;5)

      Складання таблиці «Знаходження координат точок»

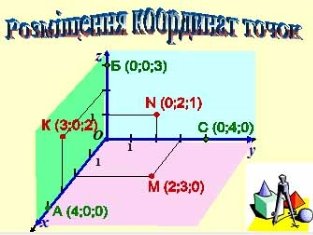
Проаналізуємо знаходження координат точок в просторі

 1. Нехай точка лежить на осі ох, координата х = 4, чому будуть дорівнювати координати у і z? В загальному вигляді  точка має такі координати А (х;0;0)

2. Нехай  точка лежить на осі оу, координата у = 4, чому будуть дорівнювати координати х і z? В загальному вигляді точка має такі координати С (0;у;z)

3. Нехай  точка лежить на осі оz, координата z = 3, чому будуть дорівнювати х і у. В загальному вигляді точка має такі координати В (0;0;z).

4. Якщо точка має координати К (3;0;2), де буде знаходитися точка? Якій площині вона належить? У загальному вигляді вона виглядає так (х;0;z).

5. Якщо точка має координати N (0;2;1), то її якій площині вона належить? У загальному вигляді вона виглядає так (0;у;z).

6. Якщо точка має координати М (2;3;0), то якій площині вона належить? У загальному вигляді вона виглядає так  (х;у;0).

Для визначення координат довільної точки A простору проведемо перпендикуляри AAx , AAy , AAz до осей Ox, Oy, Oz відповідно

Розв’язування задач (колективно,усно)

Робота в парах

Маючи таку систему координат, можна розв’язувати бага­то стереометричних задач, подібних до тих, які розв’язують за допомогою координат на площині. Зокрема, можна довес­ти такі твердження:

Відстань між точками А(x_A, у_A, z_A) і В(х_B, y_B, z_B) обчислюється за формулою .

Координати середини відрізка

Нехай А (х_A; у_A; z_A) і В(х_B; у_B; z_B) — дві довільні точки простору. Вира­зимо координати середини С відрізка АВ через координати його кінців А і В.

; ..

Розв’язування задач (колективно, письмово)

ІІІ. Підсумковий етап

 «Мікрофон»:

1. Що нового ви дізналися на сьогоднішньому уроці?
2. Поясніть, як позначаються координати точки в просторі.
3. Як називаються осі координат?
4. Як називається частина простору, що утворюється при розбитті простору координатними площинами?
5. Дано точку A(3;2;1). Вкажіть координати основ перпендикулярів, опущених з цієї точки на координатні площини.
6. Дано точку A(3;2;1). Вкажіть координати основ перпендикулярів, опущених з цієї точки на координатні осі.