Прямокутник. Його властивості та ознаки

УРОК  № 7

Тема уроку. Прямокутник. Його властивості та ознаки.

Мета уроку: формувати вміння учнів розв'язувати задачі різного рівня складності, застосовуючи означення, властивості та ознаки прямокутника.

Тип уроку: формування вмінь і навичок учнів.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

Один із учнів виконує на дошці рисунки до складеної таблиці й усно коментує їх (орієнтовно — таблиця 3).

Таблиця 3

Прямокутник. Його ознаки та властивості

Учні за готовими розв'язаннями, записаними заздалегідь на дошці, перевіряють правильність виконання домашніх задач, ви­правляють помилки, за необхідністю ставлячи питання щодо їх розв'язання.

Задача 1. Розв'язання

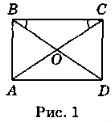
Нехай ABCD (рис. 1) — паралелограм, ОВС = ОСВ. Оскільки за умовою ОВС = ОСВ, то трикутник ОВС — рівнобедрений з осно­вою ВС, тоді ОВ = ОС. Але ABCD — паралелограм, отже, OB = OD, ОС = ОА, тому     BD = АС. Таким чином, паралелограм ABCD — пря­мокутник за ознакою.

Задача 2. Розв’язання

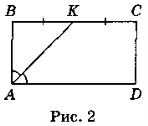
Нехай ABCD (рис. 2) — прямокутник, АК— бісектриса кута BAD, ВК = КС, АВ = 10 см. Оскільки ABCD — прямокутник, то А = 90°. Оскільки АК — бісектриса кута А, то, BAK = KAD = 45°. Тоді ВКА = 90° - 45° = 45°, отже, трикутник АВК — рівнобедрений з основою АК і АВ = ВК = 10 см. Таким чином, ВС = 20 см, тому що за умовою ВК = КС. P_ABCD = 2(АВ + ВС) = 2 · (10 + + 20) = 60 см.

Відповідь: 60 см.

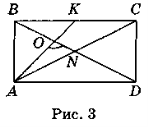
Задача 3. Розв'язання

Нехай ABCD (рис. 3) — прямокутник, BD і АС — його діагоналі, АК — бісектриса кута A, AOD = 105°. Оскільки АК — бісектриса кута BAD, то ВАК = DAK = 45°. Тоді ODA = 180° - 105° - 45° = 30° (сума кутів трикутника AOD дорівнює 180°). Оскільки ABCD — прямокутник, то AN = ND, отже, трикутник AND — рівнобедрений і NAD = NDA = 30°. Таким чином, AND = 180° - 60° = 120° .

Відповідь: 120°.

Фронтальне опитування учнів з теорії

Питання класу

1. Дайте означення прямокутника.
2. Сформулюйте властивості прямокутника.
3. Сформулюйте ознаки прямокутника.
4. Яку властивість має медіана прямокутного трикутника, прове­дена до гіпотенузи?
5. Де знаходиться центр кола, описаного навколо-прямокутного трикутника?

III. Актуалізація опорних знань учнів

Учитель пропонує усно розв'язати задачі за рисунками, зазда­легідь підготовленими на дошці або плакаті.

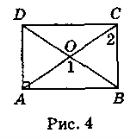
Задача 1. Дано: ABCD — прямокутник, 1 = 120° (рис. 4). Знайти: 2. (Відповідь: 60°.)

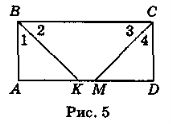
Задача 2. Дано: ABCD — прямокутник, 1 = 2, 3 = 4 (рис. 5). Довести: ВК = МС.

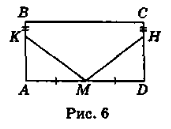
Задача 3. Дано: ABCD — прямокутник, ВК = СН, AM = MD (рис. 6). Довести: KM = НМ.

IV. Закріплення засвоєних умінь і навичок учнів

Розв'язання задач

Задача 1. У прямокутнику бісектриса кута ділить протилежну сторону на відрізки 17 см і 8 см починаючи від найближчої до цього кута вершини. Знайдіть периметр прямокутника.

Розв'язання

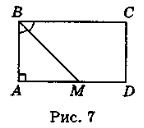
Нехай ABCD (рис. 7) — даний прямокутник, ВМ — бісектри­са кута В,     АМ = 17 см, DM = 8 см. Тоді АВМ = СВМ = 45° (ВМ — бісектриса). Отже, у прямокутному трикутнику АВМ (A = 90°) BMA = 90° - 45° = 45°. Тобто трикутник АВМ — рівнобедрений, АВ = АМ = 17 см. За властивістю протилежних сто­рін прямокутника CD = АВ = 17 см. DM = 8 см (за умовою), отже, AD = AM + MD = 17 + 8 = 25 (см). BC = AD = 25 см.

Таким чином, P_АBCD = (AB + BC) · 2 = (17 + 25) · 2 = 42 · 2 = 84 (см).

Відповідь: 84 см.

Задача 2. У прямокутнику діагональ ділить кут у відношенні 1:2, менша сторона прямокутника дорівнює 2,7 см. Знайдіть довжини діагоналей прямокутника.

Розв'язання

Нехай ABCD (рис. 8) — даний прямокутник, BD — його діаго­наль,           АВ < ВС, АВ = 2,7 см. Нехай CBD = х (х > 0), тоді ABD = 2x. Оскільки ABC = 90°, маємо: х + 2х = 90°, 3х = 90°, х = 30°. Отже, ABD = 60°, CBD = = 30°. BDA = BDC = 30° як внутрішні різносторонні при паралельних прямих ВС і AD і січній BD. Таким чином, у трикутнику ABD (A = 90°) катет АВ, що лежить проти кутав 30°, дорівнює половині гіпотенузи: АВ = BD. Отже, BD = 2АВ = 2 · 2,7 = 5,4 (см). Діагоналі прямокутника рівні, тобто АС =   = ВD = 5,4 см.

Відповідь: 5,4 см; 5,4 см.

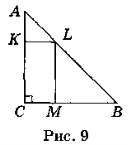
Задача 3. У прямокутний трикутник, кожний катет якого дорів­нює 6 см, вписаний прямокутник, який має із трикутником спільний кут. Знайдіть периметр прямокутника.

Розв'язання

Нехай ABC (рис. 9) — даний прямокутний трикутник, у якому С = 90°, АС = СВ = 6 см, CKLM — прямокутник. У трикутнику ABC A = B = 45°, оскільки цей трикутник рівнобедрений. Отже, у три­кутнику AKL, де AKL =    = 90° (оскільки CKLM — прямокутник), теж ALK = KAL = 45°. Таким чином, трикутник AKL — рівно­бедрений, АК = KL. Аналогічно в трикутнику LMB, де LMB = 90°, MLB = В = 45° і LM = MB.Отже, CA = CK + KA =      = CK + KL = 6 (см). Звідси P_CKLM = 2 · (CK + KL) = 12 см.

Відповідь: 12 см.

Задача 4. У прямокутнику точка перетину діагоналей знахо­диться від меншої сторони на 4 см далі, ніж від більшої. Периметр прямокутника дорівнює 56 см. Знайдіть сторони прямокутника.

Розв'язання

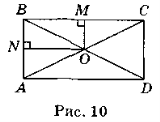
Нехай ABCD (рис. 10) — даний прямокутник, точка О — точка перетину його діагоналей. Проведемо відрізки ОМ, перпендикуляр­ний до сторони ВС, і ON, перпендикулярний до сторони АВ. Оскіль­ки ВС > АВ, то ON на 4 см більше від ОМ за умовою. У трикутнику ВОС ВО = ОС як половини рівних діагоналей АС і BD. Отже, у трикутнику ВОС висота ОМ є й медіаною (властивість висоти рівнобедреного трикутника, проведеної до основи). Тобто ВМ = ВС. Аналогічно в трикутнику BOA (ВО = ОА) точка N — середина АВ, BN = АВ . Оскільки за умовою P_ABCD = 56 см, то АВ + ВС = 28 (см), a BN + BM = 28 : 2 = 14  (см). Розглянемо чотирикутник BMON: у ньому три прямі кути, отже, BMON — прямокутник за ознакою. ОМ = BN = х см, тоді MB = ON = (х + 4) см. (х > 0) Отже, х + х + 4 = 14, 2х = 10, х = 5. Таким чином, BN = 5 см, тоді АВ = CD = 10 см, а ВМ = 5 + 4 = 9 (см), BC = AD = 18 см.

Відповідь: 10 см, 10 см, 18 см, 18 см.

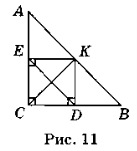
Задача 5. Гіпотенуза АВ прямокутного трикутника ABC дорівнює 8 см. Через середину гіпотенузи — точку К проведено прямі, що паралельні катетам трикутника і перетинають їх у точках D і Е. Знайдіть довжину відрізка DE.

Розв'язання

У трикутнику ABC C = 90° (рис. 11), оскільки АВ за умовою гіпотенуза. У чотирикутнику CEKD за побудовою три кути прямі. Отже, CEKD — прямокутник за ознакою. Тоді діагоналі DE і СК цього прямокутника рівні. Оскільки СК — медіана прямокутного трикутника ABC (К — середина АВ), то СК = АВ = 4 см. Таким чином, DE = 4 см.

Відповідь: 4 см.

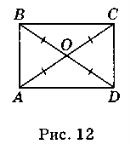
Задача 6. У прямокутнику ABCD (рис. 12) точка О — точка перетину його діагоналей,  P_ABD – P_AОD = 4 см. Знайдіть сторону АВ.

Розв’язання

P_∆ABD = AB + BD + AD. P_∆AOD = AO + OD + AD. AO = BO = OD як половини діагоналей прямокутника.

(оскільки BD = = BO + OD = AO + OD).

Відповідь: 4 см.

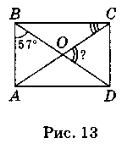
Задача 7. У прямокутнику ABCD (рис. 13) точка О — точка перетину діагоналей, ABD = 57°. Знайдіть кут COD і доведіть, що ABD + BCA =     = 90°.

Розв'язання

Оскільки ВО = АО як половини рівних діагоналей прямокутника ABCD, то трикутник АОВ — рівнобедрений. Отже, ВАО = АВО = 57° як  кути при основі рівнобедреного трикутника.  Тоді AOB = 180° - 2 · 57° = 180° - 114° =   = 66°. COD = АОВ = 66° як вертикальні.

Оскільки ABC = 90° (ABCD — прямокутник), то CBD = 90° - 57° = 33°. Трикутник ВОС — рівнобедрений з основою ВС, отже, BCA = CBD = 33°. Таким чином, ABD + ВСА = 90°, що й треба було довести.

V. Підбиття підсумків уроку

Учитель ще раз підкреслює необхідність знання всіх ознак і властивостей прямокутника та паралелограма для розв'язання задач з геометрії.

VI. Домашнє завдання

 С  1. У прямокутнику ABCD точка О — точка перетину діагоналей, AOD =   = 70°. Знайдіть кут OCD.

 Д  2. Знайдіть кут між меншою стороною та діагоналлю прямокут­ника, якщо він на 30° менший від кута між діагоналями, який лежить проти меншої сторони.

 В  3. Перпендикуляр, проведений з вершини прямокутника до діагоналі, ділить її у відношенні 3:1. Знайдіть довжину діагоналей прямокутника, якщо точка перетину діагоналей віддалена від більшої сторони на 6 см.