Прямокутний паралелепіпед і його об'єм.

Тема. Прямокутний паралелепіпед і його об'єм.

Мета: навчити розв'язувати задачі практичного і фізичного змісту на обчислення об'ємів прямокутного паралелепіпеда і куба; перевірити засво­єння геометричного матеріалу розділу «Площа прямокутника», «Об'єм прямокутного паралелепіпеда».

Тип уроку: застосування знань, вмінь та навичок.

Хід уроку

І. Актуалізація опорних знань

Усні вправи

1. Чи існує прямокутний паралелепіпед, 4 грані якого мають площі:

2 м², 3м², 4м², 5м²?

2. Скільки дроту пішло на виготовлення дротяного каркасу прямокут­ного паралелепіпеда, виміри якого дорівнюють 4 см, 5 см і 6 см?
3. Об'єм прямокутного паралелепіпеда дорівнює 120 см³. Яка з наступ­них трійок чисел може задавати виміри цього паралелепіпеда?

1) 3 см, 4 см, 5 см;

2) 4 см, 5 см, 6 см;

3) 1 см, 2 см, 10 см.

4. Скільки кубічних сантиметрів міститься в 3 дм³, 4 м³, 5 дм³, 6 см³ ?
5. У скільки разів збільшиться добуток трьох множників, якщо:

1) один з них збільшити у 2 рази;

2) один збільшити у 2 рази, а другий — у 3 рази;

3) кожний із множників збільшити у 2 рази?

II. Вдосконалення знань

Учням пропонується розв'язати задачу.

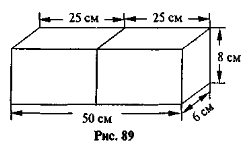Задача. Дерев'яний бру­сок, що має форму прямо­кутного паралелепіпеда, роз­різали навпіл (рис. 89). Який об'єм має кожна з утворених частин, якщо виміри бруска 6 см, 8 см і 50 см? Скількома способами можна розв'язати задачу?

 Розглянувши рисунок, мабуть, хтось з учнів запропонує одразу знай­ти об'єм правої частини, потім лівої частини. Відповідно, хтось запро­понує одразу знайти об'єм усього бруса і поділити навпіл.

Слід зробити зауваження, що обидва способи розв'язання задачі пра­вильні, але другий у цьому випадку більш раціональний, ніж перший. Але взагалі треба пам'ятати, що об'єм, так само як і площа, має таку вла­стивість: якщо якесь число поділити на частини, то сума об'ємів утворе­них частин дорівнює об'єму тіла, або якщо від тіла відрізати якусь частину об’єму V, то його (тіла) об'єм зменшиться на V.

Після цих пояснень учитель пропонує учням розв'язати задачу № 632 за підручником.

№ 632. Об'єм утвореного тіла дорівнює різниці об’єму прямокутного паралелепіпеда з вимірами 30 см, 20 см і 25 см і паралелепіпеда з вимірами 15 см, 20 см і 5 см. Тому шуканий об'єм

Відповідь. 13 500 см³.

 Далі учням пропонується розв'язати задачі № 634, 635, 638, які є ва­ріантами задач на арифметичні дії і під час розв'язання яких використо­вуються формули об'ємів куба та прямокутного паралелепіпеда.

№634.

1) V = 4³ = 64 (см³) – об'єм куба;

2) V · 7 = 448 (см³)

№ 635.

1) V = 15 000 · 80 · 60 = 72 000 000 (см³) = 72 (м³) – за 8 год;

2) 72 : 8 = 9 (м³) — виконує машина за 1 год;

3) 72 м³ = 72 000 дм³;

4) 72 000 : 240 = 300 (коротунів) заміняє Машина.

Відповідь. 300.

№ 638.

1) 12 : 2 = 6 (см) — ширина паралелепіпеда;

2) 12 : 4 = 3 (см) його висота;

3) 12 · 6 · 3 = 216 (см³) – об'єм куба і паралелепіпеда;

4) V = a³ = 216 (см³), тому оскільки 6³ = 216, то а = 6 см;

5) S = 6a² = 6 · 6² = 216 (см²) — площа поверхні куба.

Відповідь. 216 см².

III. Контроль засвоєння знань

У заключній частині уроку перевіряється рівень засвоєння теми, й учні виконують тес­тові завдання.

Варіант 1

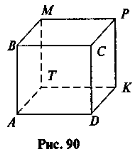
1. На рисунку 90 зображено прямокутний па­ралелепіпед. Яка з наведених граней є його нижньою гранню?
   1) ВМРС; 2) CPKD; 3) ADKT; 4) ВМТА.
2. Маємо дротяний каркас прямокутного паралелепіпеда, виміри якого 4 см, 6 см, 12 см. Скільки дроту (у см) пішло на виготовлення цього каркасу?

1) 22 см; 2) 66 см; 3) 44 см; 4) 88 см.

3. Які з наведених розмірів могли б бути трьома вимірами прямокутного
   паралелепіпеда (у см), якщо його об'єм 300 см³ ?

1) 15; 4; 6; 2) 12; 6; 5; 3) 6; 5; 10; 4) 25; 6; 4.

4. Яка з наведених рівностей неправильна?

1) 6 дм³ 5 см³ = 605 см³ ;

2) 2 м³ 3 дм³ = 2003 дм³;

3) 5 000 115 см³ = 5 м³ 115 см³;

4) 12 см³ 24 мм³ = 12 024 mm³,

5. Із заліза виплавили три куби з ребрами 3, 4 і 5 дм. Потім їх усі розпла­вити і виплавити один куб. Яка довжина ребра цього куба?

1) 12 дм; 2) 60 дм; 3) 6 дм; 4) 30 дм.

Варіант 2

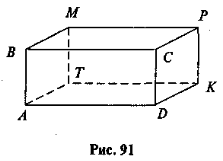
1. На рисунку 91 зображено пря­мокутний паралелепіпед. Яка з наведених граней є його пра­вою гранню?

1) DCKT; 2) АВЕМ; 3) МЕКТ; 4) ВСКЕ.

Яка з них дорівнює грані АВСD?

2. Маємо дротяний каркас прямо­кутного паралелепіпеда, виміри якого 2 см, 3 см і 5 см. Скільки дроту (у см) пішло на виготов­лення цього каркасу?

1) 15 см; 2) 20 см; 3) 40 см; 4) 30 см.

3. Які з наведених трійок чисел могли б бути трьома вимірами прямокутного паралелепіпеда (у см), якщо його об'єм 360 см³ ?

1) 12, 6, 5; 2) 9, 12, 5; 3) 15, 6, 5; 4) 8, 5, 11.

4. Яка з наведених рівностей неправильна?

1) 82 дм³ 14 мм³ = 8 200 014 мм³;

2) 5 м³ 15 дм³ = 5 015 дм³;

3) 4 дм³ 8 см³ = 4 008 см³;

4) 15 см³ 12 мм³ = 15 012 мм³.

5. Яке з наведених чисел може виражати довжину дроту (у см), потрібно­го для виготовлення каркасної моделі куба, довжина ребра якого ста­новить ціле число сантиметрів?

1) 40; 2) 96; 3) 64; 4) 94.

IV. Домашнє завдання

п. 21, № 633, 636; додатково № 642, на повторення № 645.