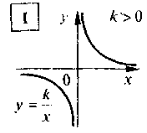
Функція у=к/х, її властивості і графік
Тема. Функція у=к/х, її властивості і графік
Мета: домогтися засвоєння учнями основних понять, пов'язаних з означенням функції у=к/х та її властивостями (вид рівняння, область визначення, область значень, вид та назва графіка цієї функції); сформувати в учнів первинні вміння: виділяти серед запропонованого списку функцій обернено пропорційні; відтворювати властивості, обернено пропорційних функцій з урахуванням знака коефіцієнта k; будувати графіки функцій, які є оберненою пропорційністю із заданим коефіцієнтом k.
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Функції».
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
Тестова робота № 4
- Який із записів є стандартним виглядом числа 0,3005?
|
А |
Б |
В |
Г |
|
3,5 ∙ 10-3 |
3,005 ∙ 103 |
3,005 ∙ 10-1 |
3,005 ∙ 10-3 |
- Укажіть порядок числа 0,353.
|
А |
Б |
В |
Г |
|
3 |
2 |
-3 |
-1 |
- В якому випадку дію (3 ∙ 10-5) ∙ (1,2 ∙ 102) виконано правильно?
|
А |
Б |
В |
Г |
|
3,6 ∙ 10-3 |
3,6 ∙ 107 |
0,36 ∙ 102 |
0,36 ∙ 10-3 |
- В якому випадку ділення виконано правильно?
|
А |
Б |
В |
Г |
|
(2∙105):(4∙102) = = 0,5 ∙ 103 |
(2∙105):(4∙102) = = 5 ∙ 102 |
(2∙105):(4∙102) = = 500 |
(2∙105):(4∙102) = = 8∙107 |
Після проведення тестової роботи обов'язково проводимо перевірку та обговорення допущених помилок.
У разі необхідності учням, які виконали роботу на недостатньо високому рівні, дається додаткове домашнє завдання: виконати роботу над помилками, підготуватися до повторної роботи з цієї теми.
III. Формулювання мети і завдань уроку
З метою створення відповідної мотивації навчальної діяльності учнів на уроці можна запропонувати їм кілька практичних (фізичних та геометричних) задач, в яких йде мова про добре відомі їм із повсякденного життя величини, залежність між якими виражається формулою виду ![]() , де k — деяке фіксоване число (константа), а x та у — саме ті величини, про які йдеться: наприклад, залежність між швидкістю руху v за прямолінійного рівномірного руху та часом руху t за умови фіксованої відстані s:
, де k — деяке фіксоване число (константа), а x та у — саме ті величини, про які йдеться: наприклад, залежність між швидкістю руху v за прямолінійного рівномірного руху та часом руху t за умови фіксованої відстані s: ![]() або залежність між шириною а та довжиною b прямокутника із фіксованою площею s:
або залежність між шириною а та довжиною b прямокутника із фіксованою площею s: ![]() і т. д.
і т. д.
Після цього цілком логічно пов'язати таку залежність з вивченим попередньо матеріалом (раціональні дроби та функціональні залежності) і поставити питання про існування та властивості загальної функції виду ![]() . Вивчення питання про означення та основні властивості функції
. Вивчення питання про означення та основні властивості функції ![]() та їх практичне застосування і становить основну дидактичну мету уроку.
та їх практичне застосування і становить основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: виконання арифметичних дій (особливо ділення) раціональних чисел; зміст та застосування термінології, пов'язаної з поняттям «функція»; оперативні вміння працювати з рівнянням, що задає функцію (за даним значенням аргументу знайти відповідне значення функції, та навпаки, знайти, при якому значенні аргументу функція набуває цього значення; перевірити обчисленням, чи належить точка із заданими координатами графіку функції, рівняння якої відоме); побудова точок із заданими координатами в декартовій системі координат, і навпаки, відшукування координат точок, зображених у системі координат.
Виконання усних вправ
- Дайте означення числової функції. Що називають аргументом функції? Значенням функції?
- Дайте означення області визначення функції; області значень функції.
- Що називається графіком функції?
- Як знайти область визначення функції?
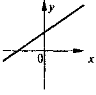
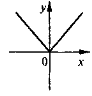
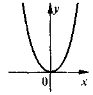
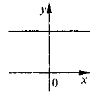
- Поставте у відповідність рисунки і рівняння функцій:
|
а) |
б) |
в) |
г) |
|
|
|
|
|
|
1) у= |х|; |
2) y = 3; |
3) y = kx + b; |
4) у = х2. |
V. Засвоєння знань
План вивчення нового матеріалу
- Означення оберненої пропорційності. Приклади.
-
Графік функції
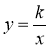 ; приклад. Як побудувати графік функції,
; приклад. Як побудувати графік функції, 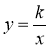 .
.
-
Властивості функції
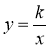 (за графіком).
(за графіком).
|
Конспект 8 |
|
|
Функції |
|
|
1. Числова функція — замість змінної .у від змінної х, за якої кожному значенню змінної х з деякої множини (область визначення функції) відповідає єдине значення v з деякої множини (область значень функції). х — аргумент; у — функція (значення функції). |
|
|
2. Найчастіше функції задають формулами. |
|
|
3. Функція виду (задана формулою) |
|
|
4. Властивості функції а) область визначення: х ≠ 0; б) множина значень: у ≠ 0; в) графік — гіпербола — крива, що складається із двох частин (віток), симетричних відносно (0;0): |
|
|
|
|
|
5. Функція у = х2 мас такі властивості:
а) область визначення: б) множина значень: у ≥ 0: (у — невід'ємне число); в) графік — парабола. |
|
Уведення поняття функції, що мас назву «обернена пропорційність», проводиться на основі практичних уявлень учнів (див. вище). Після введення означення названої функції цілком природно перейти до побудови графіків конкретних функцій ![]() (для випадку, коли k > 0 і k < 0 окремо); при цьому важливо зауважити, що оскільки дана функція не є лінійною, то і графік її не буде прямою лінією, а отже, для більш точної побудови графіка слід знайти якомога більше точок цього графіка (для більшої наочності на уроці доречним було б застосування відповідних комп'ютерних програм). Під час вивчення питання про особливості графіка функції
(для випадку, коли k > 0 і k < 0 окремо); при цьому важливо зауважити, що оскільки дана функція не є лінійною, то і графік її не буде прямою лінією, а отже, для більш точної побудови графіка слід знайти якомога більше точок цього графіка (для більшої наочності на уроці доречним було б застосування відповідних комп'ютерних програм). Під час вивчення питання про особливості графіка функції ![]() слід зробити акцепт на таких його особливостях (сприймаючи які, учні найчастіше помиляються):
слід зробити акцепт на таких його особливостях (сприймаючи які, учні найчастіше помиляються):
-
графік функції
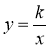 у першу чергу відповідає загальному означенню графіка функції: кожна точка цього графіка мас координатами деяке значення аргументу (взяте з області визначення функції) та відповідне значення функції;
у першу чергу відповідає загальному означенню графіка функції: кожна точка цього графіка мас координатами деяке значення аргументу (взяте з області визначення функції) та відповідне значення функції;
-
графік функції
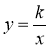 складається з двох частин, кожна з яких, розглянута окремо, є лише частиною графіка;
складається з двох частин, кожна з яких, розглянута окремо, є лише частиною графіка;
-
графік функції
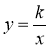 не є дугою кола (тому не можна його будувати, користуючись циркулем);
не є дугою кола (тому не можна його будувати, користуючись циркулем);
-
графік функції
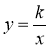 є симетричним відносно початку координат (тобто вітки графіка функції
є симетричним відносно початку координат (тобто вітки графіка функції 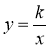 можуть бути розташовані або в І та III координатних чвертях, або в іншому випадку у II та IV координатних чвертях).
можуть бути розташовані або в І та III координатних чвертях, або в іншому випадку у II та IV координатних чвертях).
Після побудови графіків (прикладів) функцій ![]() та проведеного порівняння узагальнюємо властивості функції
та проведеного порівняння узагальнюємо властивості функції ![]() та записуємо їх у вигляді таблиці (див. опорний конспект).
та записуємо їх у вигляді таблиці (див. опорний конспект).
VI. Формування вмінь
Виконання усних вправ
- Яка із заданих функцій є оберненою пропорційністю?
а) y = 3х; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Яка область визначення функцій:
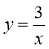 ; у = 3х;
; у = 3х; 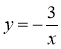 ?
?
-
В яких координатних чвертях розміщені графіки функцій:
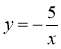 ;
; 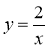 ?
?
Виконання письмових вправ
Для реалізації дидактичної мсти на цьому уроці слід розв'язати завдання такого змісту:
- Знаходження значень функції (аргументу) при даному значенні аргументу (функції).
1) Знайдіть значення функції ![]() при х = -4; х = 2; х = 8.
при х = -4; х = 2; х = 8.
2) Знайдіть значення х, при яких значення функції ![]() дорівнює: -5; --1; 15.
дорівнює: -5; --1; 15.
3) Функцію задано формулою ![]() . Заповніть таблицю:
. Заповніть таблицю:
|
х |
- 4 |
|
- 0,25 |
2 |
5 |
16 |
|
|
у |
|
- 4 |
|
|
|
|
0,4 |
4) Обернену пропорційність задано формулою ![]() . Знайдіть значення функції, яке відповідає значенню аргументу, що дорівнює: 100; 1000; 0,1; 0,02. Чи належать графіку цієї функції точки: А (-0,05; -200), В (-0,1; 100), С (4О0; 0,025), D (500; -0,02)?
. Знайдіть значення функції, яке відповідає значенню аргументу, що дорівнює: 100; 1000; 0,1; 0,02. Чи належать графіку цієї функції точки: А (-0,05; -200), В (-0,1; 100), С (4О0; 0,025), D (500; -0,02)?
- Перевірити, чи належать графіку функції точки із заданими координатами (знайти невідому координату графіка функції за відомою іншою або задати обернену пропорційність, якщо відомі координати точки графіка цієї функції).
1) Чи належать графіку функції ![]() точки: А(-8; 1), В(-4; -2), С(-2;4), D(-0,5; 8)?
точки: А(-8; 1), В(-4; -2), С(-2;4), D(-0,5; 8)?
2) Відомо, що деяка функція — обернена пропорційність. Запишіть цю функцію формулою, знаючи, що значенню аргументу, що дорівнює 2, відповідає значення функції, що дорівнює 12.
3) Рухаючись зі швидкістю v км/год, потяг проходить відстань між містами А і B, яка дорівнює 600 км, за t год. Запишіть формулу, яка виражає залежність: a) v від t; б) t від v.
-
Побудова графіка оберненої пропорційності.
1) Побудуйте графік функції:
a) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , де -4 ≤ х ≤ 5 (х ≠ 0).
, де -4 ≤ х ≤ 5 (х ≠ 0).
2) Побудуйте графік функції ![]() . Користуючись графіком, знайдіть значення функції, які відповідають таким значенням аргументу: -2,5; 5.
. Користуючись графіком, знайдіть значення функції, які відповідають таким значенням аргументу: -2,5; 5.
3) Побудуйте графік функції, заданої формулою ![]() . Знайдіть за графіком:
. Знайдіть за графіком:
а) значення у, яке відповідає значенню х, що дорівнює: 4; 2,5; 1,5; -1; -2,5;
б) значення х, якому відповідає у, яке дорівнює: 8; -2.
4) Побудуйте графік функції, заданої формулою:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
5) Задайте формулою обернену пропорційність, знаючи, що її графік проходить через точку:
а) A(8; 0,125); б) В 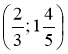 ; в) С(-25; -0,2).
; в) С(-25; -0,2).
- Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Відомо, що графік функції ![]() проходить через точку A(10; 2,4).
проходить через точку A(10; 2,4).
Чи проходить графік цієї функції через точку:
а) B(1; 24); б) С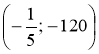 ; в) D(-2; 12)?
; в) D(-2; 12)?
2) Вставте пропущене число:
|
|
|
|
3аb2 |
2а7 – 3b |
|
12 |
? |
- На повторення: вправи на перетворення раціональних виразів, на розв'язування раціональних рівнянь.
1) Спростіть вираз 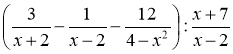 .
.
2) Доведіть, що при всіх допустимих значеннях змінних значення дробу не залежить від значень цих змінних:
а) 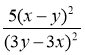 ; б)
; б) 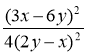 .
.
3) Розв'яжіть рівняння:
а) ![]() ; б)
; б) 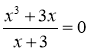 ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж)
; ж) ![]() ; з)
; з) 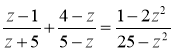 .
.
Вправи, винесені па урок, мають на меті, по-перше, сформувати в учнів уміння виділяти обернену пропорційність серед інших функцій, по-друге, вдосконалити обчислювальні навички та навички роботи із формулами, по-третє, розвивати графічну культуру учнів. Під час виконання всіх запропонованих вправ бажано вимагати від учнів коментарів із використанням матеріалу уроку.
VII. Підсумки уроку
На якому з наведених рисунків зображено ескіз графіка функції ![]() ?
?
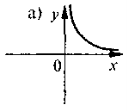

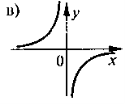
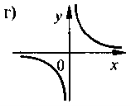
VIII. Домашнє завдання
- Вивчити означення та властивості оберненої пропорційності.
- Розв'язати вправи на застосування вивчених властивостей.
-
На повторення: означення та властивості лінійної функції; виконати
вправи на побудову графіка лінійної функції та аналітичного способу
знаходження координат точок перетину графіків лінійних функцій.


про публікацію авторської розробки
Додати розробку