РЕАЛІЗАЦІЯ НАСКРІЗНИХ ЛІНІЙ НА УРОКАХ АЛГЕБРИ

Навчання за наскрізними лініями реалізується насамперед через:організацію навчального середовища — зміст та цілі наскрізних тем враховуються при формуванні духовного, соціального і фізичного середовища навчання;навчальні предмети — виходячи із наскрізних тем при вивченні предмета проводяться відповідні трактовки, приклади і методи навчання, реалізуються проекти. Роль навчальних предметів при навчанні за наскрізними темами різна і залежить від цілей і змісту навчального предмета та від того, наскільки тісно той чи інший предметний цикл пов’язаний із конкретною наскрізною темою;предмети за вибором;роботу в проектах;позаурочну навчальну роботу і роботу гуртків.

Наскрізні лінії та їх реалізація. Наскрізні лінії є засобом інтеграції ключових і загальнопредметних компетентностей, навчальних предметів та предметних циклів; їх необхідно враховувати при формуванні навчального середовища. Наскрізні лінії є соціально значимими надпредметними темами, які допомагають формуванню в здобувачів освіти уявлень про суспільство в цілому, розвивають здатність застосовувати отримані знання у різних ситуаціях.

Математика – універсальна наука. Дійсно, її вивчення – одна із основ становлення розвиненої особистості. Дуже важливо на кожному уроці мотивувати групу і щоразу демонструвати її практичне значення, але, окрім використання на уроках математики міжпредметних зв’язків з іншими науками, можна на уроках з інших предметів використовувати математику. Теорія ймовірностей та математична статистика виступає інструментом для вивчення економічних теорій, фізики, що в свою чергу, формує компетентності здобувачів освіти у розв’язанні задач та завдань професійної спрямованості.

Наскрізна лінія «Екологічна безпека й сталий розвиток» спрямована на формування в учнів:соціальної активності, відповідальності та екологічної свідомості,готовності брати участь у вирішенні питань збереження довкілля і розвитку суспільства, усвідомлення важливості сталого розвитку для майбутніх поколінь. Проблематика наскрізної лінії «Екологічна безпека та сталий розвиток» реалізується:через завдання з реальними даними про використання природних ресурсів, їх збереження та примноження. Аналіз цих даних сприяє:розвитку бережливого ставлення до навколишнього середовища, екології,формуванню критичного мислення, вміння вирішувати проблеми, критично оцінювати перспективи розвитку навколишнього середовища і людини. Можливі уроки на відкритому повітрі. При розгляді цієї лінії важливе місце займають відсоткові обчислення, функції, елементи статистики.

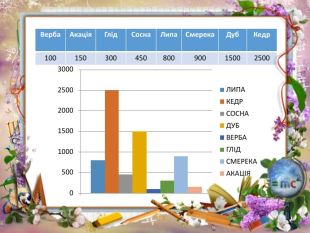
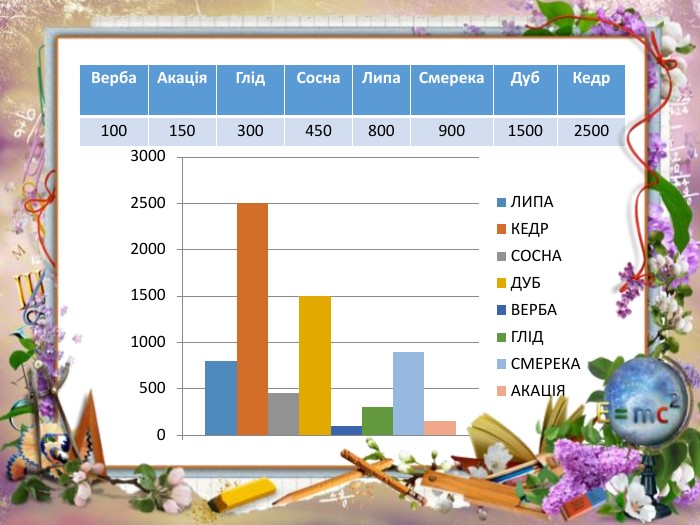
Тема. Генеральна сукупність. Графічне зображення інформації про вибірку. Тривалість життя кедра становить 2500 років, липи – 800 , сосни – 450, дуба – 1500, верби – 100, глоду – 300, смереки – 900, акації – 150 років. Впорядкуйте генеральну сукупність, записавши роки тривалості життя дерев в порядку зростання. Побудуйте гістограму тривалості життя дерев. Визначте, яке дерево довговічніше?

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Верба. Акація. Глід. Сосна. Липа Смерека Дуб Кедр 10015030045080090015002500

На уроках географії аудиторія, розв’язуючи завдання, часто звертається за допомогою до математичного апарату. Задача. Якою буде подія: вірогідна, неможлива чи ймовірна: в цьому році 12 жовтня температура повітря вночі буде +20 С, якщо в минулому і позаминулому роках була 00 С і +20 С. Для розв’язання даної задачі необхідно учням згадати теорію ймовірностей, пригадати які події називають ймовірними, які неможливими, а які вірогідними. А ще діждатися 12 жовтня.

  Реалізація змістової лінії «Громадянська відповідальність» сприяє формуванню відповідального члена громади і суспільства, що розуміє принципи і механізми функціонування суспільства. Ця наскрізна лінія освоюється в основному через колективну діяльність (дослідницькі роботи, роботи в групі, проекти тощо), яка поєднує математику з іншими навчальними предметами і розвиває в учнів готовність до співпраці, толерантність щодо різноманітних способів діяльності і думок. Україна – це наша рідна земля. А земля кожної держави - її недоторкана власність, яку вона готова обороняти, від посягань ворогів. Україна – наша Батьківщина, вона має свою землю, свою мову, культуру, історію, власні звичаї і традиції. І від нас залежить якою вона буде в майбутньому

Гурткова робота Оскільки ми говоримо про міжпредметні зв’язки, то доречним буде розробити проект дослідження, спираючись на актуальні питання іншої предметної діяльності. В процесі проектної діяльності важливо, що учні не лише розв’язують проблемні питання поставлені викладачем, а й самостійно розробляють прикладні задачі, що вказуватиме на якісне володіння теоретичним матеріалом теми. Тому можна запропонувати розробити проект «Ймовірність події у моєму житті», об’єднавши аудиторію у три групи. I група – метеорологи (вони досліджуватимуть ймовірність опадів, сонячної погоди на кожен день тижня, роблячи висновки, який одяг одягати, як підготувати себе до настання події); ІІ група – господарі (досліджуватимуть ймовірності подій, які можуть виникати у справах по дому); ІІІ група – робітники (досліджуватимуть ймовірності подій, які виникатимуть у виробничих процесах).

У творах класиків ми можемо спостерігати приклади випадкових подій, стохастичних процесів. Так у творах Тараса Григоровича Шевченка є приклади: ● попарно несумісних подій: «Мені однаково, чи буду Я жити в Україні, чи ні. Чи хто згадає, чи забуде Мене в снігу на чужині – Однаковісінько мені…»; ● суми та добутку подій: «Як умру, то поховайте мене на могилі…». Ці приклади можемо використовувати на уроках алгебри, при поясненні теоретичного матеріалу теми «Елементи комбінаторики» для закріплення на конкретних завданнях

№1. Під час стріляння з автоматичної зброї відносна частота влучень у ціль дорівнює 0,95. Знайти кількість влучень, якщо зроблено 160 пострілів.(152) №2. Для руйнування моста достатньо влучення однієї авіаційної бомби. Знайти ймовірність того, що міст буде зруйновано, якщо на нього скинули 3 бомби та ймовірності влучення яких відповідно дорівнюють 0,6; 0,7 та 0,9.(0,988) №3. Після бурі на ділянці між 20-м та 45-м кілометрами лінії електропередачі відбувся обрив провода. Яка ймовірність того, що обрив відбувся між 30-м і 40-м кілометрами лінії?(0,4)

Підведення підсумків1) Із букв слова «Україна» почали створювати нові українські слова і записувати кожне з них на картки. Яка ймовірність витягнути слова, що складаються з 4 букв?2) Одного з робітників Бердянської фірми відправляють у відрядження до іншої області(що знаходиться на підконтрольній території України). Яка ймовірність того, що його направлять до області на букву «В»?3) Нехай A — множина букв у слові «Україна». Множина букв якого слова є підмножиною множини A:кара; 4) руїна; 7) кран; 10) дорога;2) кран; 5) руна; 8) країна; 11) дар;3) рана; 6) рука; 9) куна; 12) кардинал?

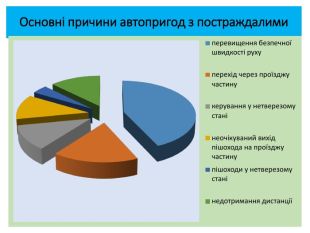
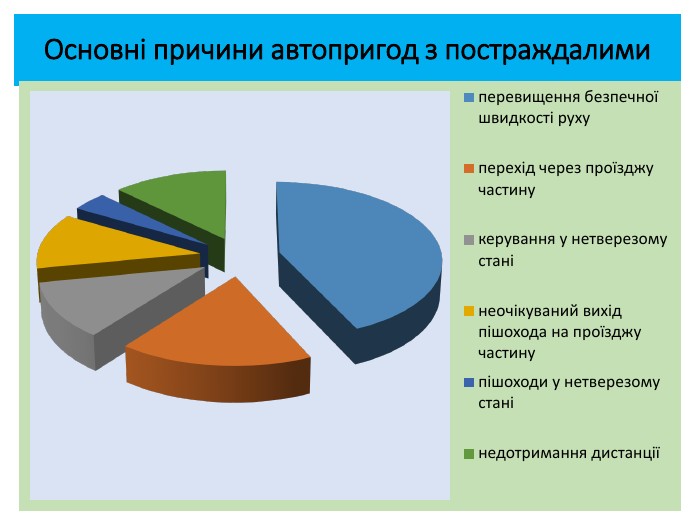
Наскрізна лінія «Здоров'я і безпека» в курсі математики реалізується через завдання з реальними даними про безпеку і охорону здоров’я (текстові завдання, пов’язані з середовищем дорожнього руху, рухом пішоходів і транспортних засобів, відсотковими обчисленнями і графіками, що стосуються чинників ризику, математичною статистикою).

На сьогоднішній день перевищення швидкості або невідповідність її конкретним дорожнім умовам є однією з основних причин скоєння ДТП у всьому світі, внаслідок яких щорічно гинуть і отримують каліцтва тисячі людей.  Причому, згідно зі статистикою ДТП, при збільшенні швидкості, тяжкість наслідків ДТП зростає в геометричній прогресії.   Україна, на жаль, не є виключенням з сумної статистики Тема: «Випадкова подія»Етап уроку: формулювання мети і завдань уроку. З якою максимально дозволеною швидкістю можна було пересуватися автотранспорту в населеному пункту до 1 січня 2018 року? 60 км/год = 16,7 м/с. А після 1 січня? 50 км/год = 13,9 м/с. Отже, різниця майже в 3 метри переміщення за секунду. МОЗ говорить про 82% смертельних випадків при зіткненні на швидкості 60 км/год, а як зміниться ймовірність летального результату при зіткненні з пішоходом при обмеженні максимально допустимої швидкості руху автотранспорту в населеному пункті 50 км/год?

Основні причини автопригод з постраждалими

Норма добової потреби у різних вітамінах складає в середньому 125 мг. Одна скурена сигарета знищує 20% вітамінів. Скільки мг вітамінів краде в себе той, хто курить?Для підлітків 12-14 років калорійність добового раціону сягає 2400-2900 ккал. Проаналізуйте, що ви сьогодні їли і обчисліть кількість ккал, що надійшли до вашого організму за добу. Визначте, скільки % свого річного доходу витрачає на сигарети людина, яка скурює одну пачку на добу, якщо пачка сигарет коштує 68 грн 50 коп.,а щомісячна зарплата становить 6700 грн

Наскрізна лінія «Підприємливість і фінансова грамотність» націлена на розвиток лідерських ініціатив, здатність успішно діяти в технологічному швидкозмінному середовищі, забезпечення кращого розуміння здобувачами освіти практичних аспектів фінансових питань (здійснення заощаджень, інвестування, запозичення, страхування, кредитування тощо). Ця наскрізна лінія пов'язана з розв'язуванням практичних задач щодо планування господарської діяльності та реальної оцінки власних можливостей, складання сімейного бюджету, формування економного ставлення до природних ресурсів.

Бінарний урок (з елементами професійної направленості, для учнів професії«Тракторист, водій, слюсар з ремонту автомобілів») «Розв’язування задач на застосування основних теорем теорії ймовірностей та наслідків з них»Задача 1 Кожна із трьох систем двигуна може вийти з ладу протягом робочої зміни незалежно одна від одної. Несправність хоча б однієї із систем призводить до поломки двигуна. Кривошипно-шатунний механізм псується з ймовірністю 0,1, система живлення з ймовірністю 0,2, газорозподільний механізм з ймовірністю   0,3. Яка ймовірність того, що двигун зіпсується протягом робочої зміни ? Перед розв’язуванням цієї задачі повторюємо з учнями:-         які події називаються незалежними в сукупності?-         чому дорівнює ймовірність появи кількох подій, незалежних у сукупності?-         сформулювати означення подій, протилежної до даної.                                  Розв’язування задачі 1 (колективно, один учень записує на дошці)Нехай А1 – подія, що полягає в тому, що кривошипно-шатунний механізм псується з ймовірністю 0,1. Ᾱ1 –протилежна до події А1  , Р(А1 ) – ймовірність події А1, Р(А1 ) = 1 - Р(Ᾱ1  ) Р(А1 ) = 1 - 0,1 = 0,9. А2 – система живлення псується з ймовірністю 0,2,  Ᾱ2-  подія, протилежна до А2 Р (А2 ) =1- Р(Ᾱ2 )=1- 0,2=0,8 А3 – газорозподільний механізм псується з ймовірністю 0,3, Ᾱ3 – подія, протилежна до А3   Р (А3 ) =1 - Р (Ᾱ3 ) =1 - 0,3 = 0,7 А – подія, яка полягає в тому що двигун зіпсується протягом робочої зміни. Р (А) – ймовірність події А. Р(А) =1 - Р (Ᾱ1 ) Р( Ᾱ2 ) Р(Ᾱ3 ) Р(А) =1 -  0,9*0,8*0,7 =1 0,504=0,496. Отже, двигун зіпсується протягом робочої зміни з ймовірністю 0,496,  якщо хоча б одна із трьох систем вийде з ладу.                  

Задача. Вкладник поклав до банку 10000 грн. під 12% річних. Через скільки років сума на рахунку подвоїться?Розв’язання: Так як мова йде про нарахування річних відсотків за депозитним вкладом, то у відповіді може бути лише ціле число років. За правилами округлення це 6. Але за шість років сума на рахунку буде, хоч і не на багато, але менша за подвійну. Тому вкладнику необхідно чекати 7 років. Відповідь: вклад подвоїться через 7 років