Решение иррациональных уравнений с использованием равносильных преобразований

Тема урока: " Решение иррациональных уравнений                                                                                        с использованием равносильних преобразований( возведение в степень с учетом ОДЗ, используя определение и свойства корней)".

Цели урока.

1.возместить отсутствие единого обобщения по данной теме в курсе алгебры 10-го класса;

2.повторить основные теоретические понятия;

3.закрепить основные способы решения иррациональных уравнений;

Ход урока

І.Изложение нового материала.

Иррациональные уравнения.

Определение. Уравнение с одной переменной f(x)=g(x) называется иррациональным, если хотя бы одна функция f(x) или g(x) содержит переменную x под знаком радикала.

При решении иррациональных уравнений используют тождественные преобразования, применяют метод возведения в степень с учетом ОДЗ, используя определение и свойства корней)".

Теорема. Если возвести обе части уравнения f(x)=g(x) в натуральную степень n, то полученное уравнение fn(x)=gn(x) является следствием данного уравнения.

Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту же чётную степень, расширение области определения и др. По этим причинам необходимой частью решения иррационального уравнения является проверка, либо использование области определения заданного уравнения.

1. Метод возведения обеих частей уравнения в одну и ту же степень с учетом ОДЗ.

Пример 1. Решить уравнение

Решение. Возведя обе части уравнения в квадрат, получим

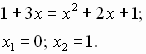
Сделав проверку, убеждаемся, что оба они являются его корнями. Это уравнение служит примером того, что возведение в квадрат исходного уравнения не всегда приводит к появлению посторонних корней.

Ответ.

Пример 2. Решить уравнение

Решение. Найдём область определения уравнения: [2; ?). Возведём обе части уравнения в квадрат, уединим затем полученный радикал и возведём ещё раз в квадрат. Получим корни уравнения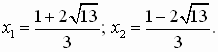

После проверки получим корень уравнения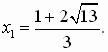

Ответ: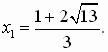

Пример 3. Решить уравнение

Решение. Уравнение перепишем так:

  Возведём обе части в квадрат, получим

x=2 проверить нетрудно, а проверять громоздко. Однако заметим, что при этом значении отрицательно. Значит,  не является решением уравнения.

Ответ: х=2.

ІІ.Устно.

Доказать, что уравнения не имеют корней:

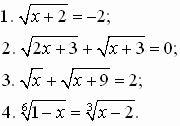
ІІІ.Дополнительные уравнения.

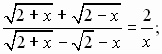
ІV. Домашнение задание.

=3