Річна Контрольна робота з геометрії для 7 класу

Річна контрольна робота з геометрії для 7 класу

Завдання 1-6 мають 4 варіанти відповідей, серед яких один правильний.

1.     (0,5 бала) Точка К – середина відрізка ВС, точка Р – середина відрізка КС. Знайдіть довжину відрізка ВР, якщо РС = 14 см.

2.     (0,5 бала) Один із суміжних кутів дорівнює 75^о. чому дорівнює другий кут?

3. 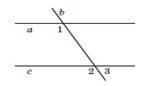    (0,5 бала) На рисунку прямі а і с паралельні, в – січна, ∠ 1 = 126^о, Знайдіть ∠3.  

4.     (0,5 бала) У трикутнику MKP  KN – висота. Яке з наведених тверджень правильне?

5.     (0,5 бала) Периметр рівнобедреного трикутника дорівнює 40 см. Знайдіть основу трикутника, якщо бічна сторона дорівнює 15 см.

6.     (0,5 бала) Коло радіусом 5 см описане навколо трикутника. Чому дорівнює відстань від центра кола до кожної з вершин трикутника?

7.     (1,5 бала) Встановіть відповідність між елементами трикутників (1 – 4) і їх видами (А – Д).

8.     (1,5 бала) Встановіть відповідність між видом трикутника (1 – 4) та кількістю кутів (А – Д), які необхідно знати, щоб можна було визначити невідомі кути цього трикутника.

9.     (3 бала) У трикутнику АВС відомо, що ∠ ВАС = 56^о. Бісектриса кута ВАС перетинає сторону ВС у точці Р, ∠ АРС = 104^о. Знайдіть кут АВС та зовнішні кути трикутника.

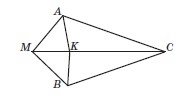
10. (3 бала) Доведіть рівність кутів АСК і ВСК, що зображені на рисунку, якщо АК = ВК і АМ = ВМ.

Відповіді 

1. В 2. Б 3. В

4.     В

5.     А

6.     Б

7.     1(Г), 2(А), 3(Б), 4(В).

8.     1(Б), 2(Г), 3(А), 4(В).

9.     Дано: ⊿ АВС

           ∠ ВАС = 56^о

                          ВР – бісектриса ∠ ВАС

                               ∠ АРС = 104^о

                Знайти: ∠ АВС, ∠ 1, ∠ 2, ∠ 3 (зовнішні)

Розв’язання

Так як ВР є бісектрисою ∠ ВАС за умовою, то ∠ РАС = 56^о : 2 = 28^о. Роздивимось

⊿АРС, в якому зможемо знайти ∠ АСР.

 ∠ АСР = 180^о – (104^о + 28^о) = 48^о

∠АВС = 180^о – (56^о + 48^о) = 76^о

∠1= 76^о + 48^о = 124^о

∠ 2 = 56^о + 48^о = 104^о

∠ 3 = 76^о + 56^о = 132^о

Відповідь : ∠АВС = 76^о, ∠1 = 124^о, ∠ 2 = 104^о, ∠ 3 = 132^о.

10.  Доведення повинно бути обґрунтовано, всі ознаки, за якими відбувається доведення, записувати повністю.