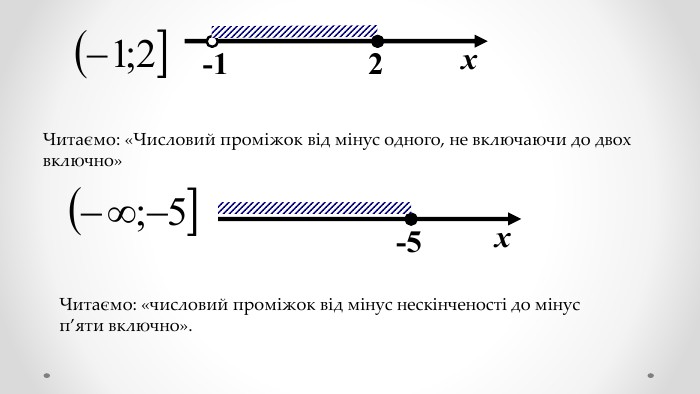
Рівносильні нерівності, числові проміжки
Про матеріал
Додатковий матеріал до уроку "Рівносильні нерівності, числові проміжки" для дітей з порушеннями слухової функції. Можливе використання для дистанційного навчання. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку