Матеріали для спецкурсу "Алгебра та початки аналізу 10-11клас" "Тригонометричні рівняння виду asin x + bcos x = c "

Тригонометричні рівняння виду

asin x + bcos x = c

Матеріали для проведення

                                                 занять спецкурсу

Алгебра та початки аналізу

10-11клас

 

Вчитель математики

Войтюк Н.Н.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Передмова.

Цей посібник містить докладну теорію для розв’язування рівнянь виду asinx + bcosx = c, приклади розв’язування рівнянь даного типу різними способами та аналіз відповідей записаних у різних формах.

Розробка укладена відповідно до вимог програми курсу за вибором для 10-11 класів « Рівняння в курсі алгебри». Матеріали посібника можуть бути корисними вчителями, які викладають алгебру та початки аналізу в 10-11 класах та учнів старших класів при підготовці до ДПА та ЗНО.

Посібник для вчителів математики нового покоління.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

   Означення. Рівняння виду a sin x +b cos x = c, де a, b, c – числові коефіцієнти, називають лінійними відносно sin x та cos x.

Дане рівняння при а = b = 0 і c ≠ 0 не має коренів;

при а = 0 або b = 0 і c ≠ 0 буде найпростішим;

при а = b = c = 0 його коренями є всі дійсні числа.

Розв’яжемо рівняння в якому а ≠ 0, b ≠ 0, c ≠ 0.

Розглянемо способи розв’язування такого рівняння.

   I спосіб. Зведення даного рівняння до однорідного рівняння другого степеня відносно sin і cos .

a sinx +b cosx = c.

 2a sin · cos + b(cos²   - sin² ) = c (cos²  + sin²  );

2a sin cos + b cos² – b sin² – с cos² - с sin² = 0;

(b + с) sin² 2а sin cos + (с - b ) cos² = 0.

Розділивши обидві частини отриманого рівняння на cos² одержимо рівняння виду

a₁ tg² + а₂ tg +а₃ = 0, яке зводиться до квадратного.

При даному способі розв’язування необхідно перевіряти, чи розв’язки рівняння cosx = 0 не є коренями вихідного рівняння.

   II спосіб. Розв’язування за допомогою універсальної підстановки.

a sinx +b cosx = c.

Формули, що виражають тригонометричні функції через тангенс половинного аргументу, називають формулами універсальної підстановки.

Використавши формули sinx = 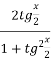та cosx = 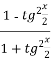зведемо його до квадратного відносно tg .

а tg² + b tg = с.

Ввівши заміну tg = t, отримаємо квадратне рівняння.

а t² + b t = с.

Звертаємо увагу , що використання універсальної підстановки може привести до звуження області допустимих значень змінної х, а саме можуть виключитися точки виду x = π + 2πk, k є Z в яких tg не визначений, тому при розв’язуванні рівнянь цим способом треба обов’язково перевіряти, чи не має воно коренів серед чисел виду

 x = π + 2πk , k є Z.

   III спосіб. Розв’язування за допомогою введення допоміжного кута.

a sin x +b cos x = c.

Поділимо ліву та праву частини рівняння на вираз . Отримаємо рівняння

sinx + cosx = .

Оскільки ( )² + ()² = 1, то існує такий кут φ, для якого

sinφ =, cosφ =

sinφ cos x + cosφ sin x =.

sin(x + φ) = .

Це рівняння, як і початкове, має розв’язки тільки в тому випадку, коли 

≤ 1, або c² ≤ a²+b² .

При виконанні цієї умови розв’язок початкового рівняння матиме такий вигляд:

x = - φ + ( arcsin + kπ, k є Z де допоміжний кут φ визначається із системи

.

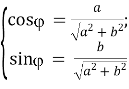Формулу asinх + bcosx = sin(x + φ ) називають формулою допоміжного кута.

При перетворенні початкового рівняння можна користуватися не тільки формулами  sin(x ± φ ), а і cos(x ± φ).

VI спосіб. Розділимо дане рівняння на а ≠ 0. Одержимо:

 sinх + cosx = .

Нехай φ = arctg . Тоді = tgφ і рівняння прийме вигляд

sinх +cosx = .

sinх + cosx = , або sin(x + φ ) = .

Якщо ≤ 1, то рівняння має розв’язок

x + φ = ( arcsin( ) + kπ, k є Z і

x = ( arcsin ( ) - φ + kπ, k є Z.

Зауваження. Провести аналіз розв’язків рівняння можливо за алгоритмом:

1. Якщо a² + b² < c² , тоді рівняння коренів не має.
2. Якщо a² + b² ≥ c² та c ≠ -b , то рівняння має один корінь.
3. Якщо a² + b² = c² , то рівняння має дві множини розв’язків і одна з яких

х = + 2k, k є Z.

Розглянемо приклади.

Приклад 1.

Розв’язати рівняння sinх + cosx = 1.

Розв’язання:

У даному рівнянні а=в=1.

Поділивши обидві частини на =, маємо

sinх + cosx = ;

sinх cos + cosx sin =;

sin (х+) = ;

 х+ = (-1)^k  + πk, k є Z,

х = (-1)^k    -  + πk, k є Z.

Відповідь: х = ( -1)^k   -  + πk, k є Z.

Приклад 2.

Розв’язати рівняння 4sinх - 3cosx = 1.

Розв’язання:

Оскільки = 5, то рівняння зводиться до вигляду

sinх - cosx = ,

sin(х + φ) = ,

Допоміжний кут φ визначаємо із системи

.

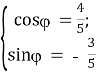Зі значень φ = - arccos та φ = arccos беремо φ = - arccos, бо в системі > 0, 0, звідки φ – кут IV чверті.

Розв’яжемо рівняння sin(х + φ) =

х + φ = ( -1)^k arcsin + πn, n є Z

х = (-1)^k arcsin + φ + πn, n є Z 

х = (-1)^k arcsin + φ + πn, n є Z

х = (-1)^k arcsin + arccos + πn, n є Z .

Відповідь: х = (-1)^k arcsin + arccos + πn, n є Z.

Приклад 3.

Розв’язати рівняння 2sinх + 3cosx = 4.

Розв’язання:

Оскільки < 16,  то дане рівняння розв’язків не має.

Відповідь: розв’язків немає.

Приклад 4.

Розв’язати рівняння 3sin5х - 2cos5x = 3.

Розв’язання:

Використавши формули sinx= 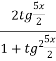та cosx = 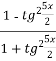отримаємо рівняння

3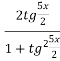 - 2 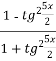-3 = 0,

tg² - 6 tg +5 = 0.

Ввівши заміну tg = t , отримаємо квадратне рівняння:

t² - 6 t +5 =0,

t = 1,                                                                         t = 5;

tg = 1,                                                                   tg = 5,

= + πn,  n є Z                                                     = аrctg5 + πn, n є Z

х = + , n є Z                                                  х = аrctg5 + , n є Z .

При даному способі розв’язування можуть бути загублені розв’язки виду х = π + 2πn, тому в дане рівняння підставимо х = π .

3sin π - 2cos π = 3,

0 -2∙ (-1) = 3,

2 ≠ 3, отже числа виду х = π + 2πn коренями даного рівняння не є.

•Приклад 5.

Розв’язати рівняння 5sinх - 4cosx = 4.

Розв’язання:

5sinх - 4cosx = 4,

а = 5; b = -4; c = 4.

Провіряємо , чи числа виду

х = π + 2πn, n є Z є розв’язками даного рівняння.

5sin(π + 2πn) - 4cos(π + 2πn) = 4,

5∙0 – 4 ∙ ( -1) = 4,

4 =4, отже числа виду х = π + 2πn є коренями даного рівняння.

Використавши формули sin x = 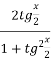, cosx =  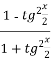зведемо його до квадратного відносно tg .

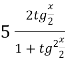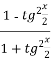- 4 = 4.

Ввівши заміну tg = t, отримаємо квадратне рівняння.

- 4 = 4,

10t - 4t + 4t² – 4 - 4t² = 0,

10t = 8,

t = 0,8,

х = 2 аrctg0,8 + 2πn, n є Z.

Відповідь: х = 2 аrctg0,8 + 2πn,

х = π + 2πn,  n є Z.

Вправи.

Розв’язати рівняння:

1. sinх - cosx = -1;
2. sin3х – 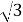cos3x = ;
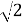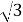3. sin2х – cos2x = 1 ;
4. 2sinх + cosx = 2;
5. sin2х - 2cos2x = 1;
6. 3sinх +4 cosx = 2;
7. sinх +7cosx = 5;
8. sin2х - cos2x = 1;
9. 3sinх - 4cosx = 0.

 

Заняття спецкурсу

Тема: Розв’язування рівнянь виду asin x +bcos x = c.

 

Навчальна мета: поглибити та розширити знання учнів про тригонометричні лінійні рівняння відносно sinх та cosx, формувати вміння та навички розв’язувати їх різними способами, вміти аналізувати отримані результати.

  Розвиваюча мета:формувати вміння відстоювати свою думку; розвивати мислення, увагу, пам'ять через постійне звернення до знань учнів .

Виховна мета: виховувати впевненість у власних знаннях та діях, стисло та переконливо аргументувати свої думки; розвивати інтелектуальні здібності.

Девіз:       Три шляхи ведуть до знання:

                  Шлях роздумів – це шлях найблагородніший,

                  Шлях наслідування - це шлях найлегший,

                  І шлях досвіду - це шлях найважчий.

Конфуцій

Обладнання: мультимедійний проектор, картки.

Організація класу

Клас об’єднався в три гетерогенні групи, які отримали завдання: розв’язати рівняння 3sinх + 4cosx = 5 різними способами.

Хід заняття

1. Організаційний момент.

Шановні учні! Звернемо увагу на слова китайського філософа Конфуція, записані на дошці.

Тож який шлях обираєте Ви?

2. Мотивація навчальної діяльності.

      Сьогодні від вас буде потрібно: вміння міркувати, виконуючи кожне завдання, і вміння наслідувати ( тобто ви маєте точно відтворити тригонометричні формули та вміти їх застосовувати), і досвід (продемонструвати вміння розв’язувати тригонометричні рівняння уже відомими способами).

     Сподіваюся, що всі ці шляхи дійсно приведуть вас до знань, які дозволять вам у майбутньому успішно скласти ЗНО і продовжити свою освіту у вишах.

III. Повідомлення теми та мети уроку.

   Тема сьогоднішнього уроку «Розв’язування рівнянь виду

 asin x +bcos x = c». Проведемо це заняття у вигляді «каруселі», кожна група буде розв’язувати одне й те саме рівняння, власним способом, а потім пояснить його іншим групам, а потім всі разом обговоримо отримані результати та зробимо висновки.

 

IV. Актуалізація опорних знань.

   Давайте пригадаємо деякі формули, знання яких нам сьогодні знадобляться.

 

• Індивідуальна робота біля дошки

Один учень записує формули співвідношення між sinx, cosx та tg , а інший формули подвійного кута.

• Фронтальна бесіда з учнями  

 Які основні типи тригонометричних рівнянь ви знаєте?

 Які способи їх розв’язання ви вмієте застосовувати?

Потім перевіряються формули записані учнями на дошці, за потреби виправлення помилок.

 

V. Удосконалення вмінь і навичок розв’язувати тригонометричні рівняння.

   Гетерогенні групи отримують завдання розв’язати рівняння

 3sinх + 4cosx = 5.

1 група.   Розв’язати рівняння 3sinх + 4cosx = 5.

Розв’язання.

Зведемо рівняння 3sinх + 4cosx = 5 до однорідного відносно sin і cos

6 sin· cos +4 (cos² - sin² ) = 5 (cos² + sin² ),

9 sin² - 6 sin· cos + cos² = 0, звідки

9 tg² - 6 tg +1= 0,

tg= t ,

9 t² - 6 t+1= 0,

(3 t – 1)²=0

3 t – 1=0,

 t = ,

,

= arсtg + πn, n є Z,

х = 2 arсtg + 2πn, n є Z.

Відповідь: х = 2 arсtg + 2πn, n є Z.

2 група  Розв’язати рівняння 3sinх + 4cosx = 5.

Розв’язання.

Застосуємо формули sin x = ,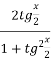

cosx = 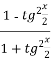 . Зведемо його до квадратного відносно tg   .

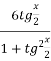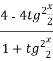+ =5.

Ввівши заміну tg = t, отримаємо  рівняння

  + = 5,

9t² - 6t + 1 = 0, t = ,

,

= arсtg + πn, n є Z,

х = 2 arсtg + 2πn, n є Z.

При даному способі розв’язування можуть бути загублені розв’язки виду х = π + 2πn, n є Z,  тому в дане рівняння підставимо х = π +2πn, n є Z .

3sin(π +2πn) + 4cos(π +2πn) = 5,

3∙0 + 4∙( -1) =5,

 -4 ≠ 5, отже числа виду π + 2πn, n є Z розв’язками даного рівняння не є.

Відповідь: х = 2 arсtg + 2πn, n є Z.

3 група.   Розв’язати рівняння 3sinх + 4cosx = 5.

Розв’язання.

Запишемо рівняння у вигляді

sinх + cosx = .

Нехай arctg = φ. Тоді = tgφ і рівняння прийме вигляд

sinх + tgφ cosx = або

sinх + cosx = ,

) = .

Оскільки = ,

= ,

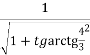= , то

 ) = 1,

= + 2πn, n є Z,

= - +2πn, n є Z,

= - +2πn, n є Z, або

 

= +2πn, n є Z.

Відповідь: = +2πn, n є Z.

Зауваження. Ще раз звернемо увагу на той факт, що при розв’язуванні рівняння різними способами одержали на перший погляд різні відповіді. Насправді ж ці відповіді співпадають.

Покажемо, що = 2 arсtg .

<   і  0 < 2 arсtg .

Окрім того, tg( = tg (2 arсtg ) .

tg( .

tg (2 arсtg )= = = .

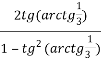Таким чином одержали відповідь:

= +2πn, n є Z або

х = 2 arсtg + 2πn, n є Z.

Пропоную розглянути ще один із способів розв’язання рівняння

3sinх + 4cosx = 5.

Розв’язання.

Оскільки = 5, то рівняння зводиться до вигляду

sinх + cosx = 1;

sin(х + φ) = 1.

х + = + 2πn, n є Z;

х = - φ + + 2πn, n є Z;

φ = arcsin або φ = arccos , отже

х = - arccos + 2 arсtg + 2πn, n є Z.

Відповідь: х = - arccos + + 2πn, n є Z.

VI. Різні способи розв’язування тригонометричного рівняння

sinх - cosx = 1.

Розв’язати рівняння sinх - cosx = 1.

Розв’язання:

1-й спосіб. За допомогою введення допоміжного кута.

У даному рівнянні а=в=1.

Поділивши обидві частини на =, маємо

sinх - cosx = ;

sinх cos – cosx sin =;

sin (х- ) = ;

 х+ = (-1)^k  + πk, k є Z,

х = (-1)^k    -  + πk, k є Z.

Відповідь: х = (-1)^k   -  + πk, k є Z.

2-й спосіб. Шляхом зведення до однорідного тригонометричного рівняння другого степеня відносно sin і cos.

Використавши формули подвійного аргументу та основну тригонометричну тотожність. Запишемо рівняння у вигляді:

2 sin cos ⁺ (cos² - sin² ) = sin² + cos² ,

звідки 2sin cos - cos² + sin² - sin² - cos² =0,

2sin cos - 2cos² =0;

2 cos (sin  - cos ) =0;

cos = 0 , або sin  - cos= 0.

Розв’яжемо отримані рівняння.

cos = 0; = + πn, n є Z; х = π + 2πn, n є Z;

Розв’яжемо рівняння sin  - cos= 0.

tg - 1= 0 ;

tg = 1;

= + πn, n є Z;

х = + 2πn, n є Z.

Відповідь: х = π + 2πn, х = + 2πn, n є Z.

3-й спосіб. Розкладання на множники лівої та правої частин рівняння.

sinх - cosx = 1,

sinх = cosx + 1,

2sin cos = 2cos²,

2sin cos - 2cos² =0;

2 cos (sin  - cos ) =0.

Отримали рівняння яке розглянули в другому способі.

4-й спосіб.  Зведення до квадратного рівняння відносно однієї з функцій.

sinх - cosx = 1,

± – cosx = 1,

± = cosx + 1.

Піднесемо обидві частини рівняння до квадрата

= 1+2 cosx + cos² x,

2cos² x+ 2 cosx = 0,

2cos x( cosx + 1) = 0,

2cos x = 0 ,           або   cosx + 1 = 0,

cos x = 0,                       cosx = - 1 ,  

х = + πn, n є Z,          х = π + 2πn, n є Z.

Піднесення до квадрата могло привести до появи сторонніх коренів, тому необхідно провести перевірку.

Отримані розв’язки можна розбити на три групи

х₁ = + 2πn, n є Z,   

х₂ = - + 2πn, n є Z,      

 х₃ = π + 2πn, n є Z.

х₁  та х₃ співпадають із раніше отриманими, тому не є сторонніми.

Перевіримо х₂ = - + 2πn, n є Z,

sin(- + 2πn) – cos(- + 2πn) = 1,

-1- 0 = 1,

-1 ≠ 1, отже х₂ = - + 2πn, n є Z  - сторонній корінь.

   Відповідь: х = π + 2πn, х = + 2πn, n є Z.

5-й спосіб. Піднесення до квадрата обох частин рівняння.

sinх - cosx = 1,

(sinх – cosx) ² = 1,

sin² - 2sin cos ⁺ cos² =0,

1 - 2sin cos = 0,

1 – sin2х = 1,

sin2х = 0,

2х = πn, n є Z,   

х = ,  n є Z.

Перевіримо, чи ми не одержали сторонні корені. 

   Отримані розв’язки можна розбити на чотири групи

х₁ = + 2πn, n є Z,   

х₂ = - + 2πn, n є Z,      

х₃ = π + 2πn, n є Z,

х₄ = 2πn, n є Z.

х₁  та  х₃ співпадають із раніше отриманими, тому не є сторонніми.

Перевіримо  х₂ = - + 2πn, n є Z,

sin(- + 2πn) – cos(- + 2πn) = 1,

-1- 0 = 1,

-1 ≠ 1, отже х₂ = - + 2πn, n є Z  -  сторонній корінь.

Перевіримо х₄ = 2πn, n є Z,

sin (2πn) – cos (2πn) = 1,

0 -1= 1,

-1 ≠ 1,отже х₄ = 2πn, n є Z  -  сторонній корінь.

   Відповідь: х = π + 2πn, х = + 2πn, n є Z.

6-й спосіб. Графічний спосіб.

sinх - cosx = 1,

Запишемо дане рівняння у вигляді sinх = cosx + 1.

Побудуємо графіки функцій y₁ = sinх та  y₂ =  cosx + 1 в одній системі координат.

Абсциси точок перетину цих графіків будуть розв’язками даного рівняння.

Відповідь: х = π + 2πn, х = + 2πn, n є Z.

VI. Підсумок заняття.

Розв’язавши одне й те саме  рівняння різними  способами ми отримуємо  одні й ті самі корені , проте з різною формую їх запису.

Отже вибір способу розв’язання рівнянь виду asin x +bcos x = c залежить тільки від ваших знань та бажань!

 

 

 

 

 

 

 

 

Література

1.Тригонометрія. О. Гайштут Р. Ушаков – Київ, « Магістр»,1997.

2. Пометун О., Пироженко Л. Сучасний урок. Інтерактивні технології навчання. – Київ., „А.С.К.”,2006.

3. „Алгебра і початки аналізу” , 10, Профільний рівень. Автори А.Г. Мерзляк, Д.А, Номіровський, В.Б. Полянський, М.С, Якір - Харків, „Гімназія”, 2010.

4. Алгебра і початки аналізу”, 10, Василь Кравчук – Тернопіль. „Підручники і посібники”, 2005.

5. Алгебра. 10 клас. Самостійні і контрольні роботи - м. Дніпропетровськ, 2005.

6. Алгебра і початки аналізу , 10. Збірник задач і контрольних робіт. А.Г. Мерзляк, В.Б.Полянський, М.С. Якір - Харків, „Гімназія”, 2010.

7. Алгебраїчний тренажер. А.Г. Мерзляк, В.Б.Полянський, М.С. Якір - Київ. „А.С.К.”, 1997