"Рівняння з параметрами"
Зміст
Вступ
- Теоретичні основи розв’язування рівнянь з параметрами.
- Лінійні рівняння ах +b = 0, де х – змінна, а, b – числа.
- Квадратні рівняння ах 2+ bх +с= 0, де х – змінна, а, b, с – числа,
причому а ≠0.
- Дробово - раціональні рівняння.
- Ірраціональні рівняння.
- Показникові рівняння.
- Тригонометричні рівняння.
- Логарифмічні рівняння.
Висновок
Список використаної літератури
Вступ
Завдання з параметрами відіграють важливу роль у формуванні логічного мислення та математичної культури у школярів, але їх розв’язування викликає у них значні труднощі. Це пов'язано з тим, що кожне рівняння з параметрами представляє собою цілий клас звичайних рівнянь, для кожного з яких має бути отримано розв’язок. Такі завдання пропонуються на ДПА ( для учнів, які вивчали математику за програмою профільного рівня) та ЗНО.
Актуальність даної теми визначається необхідністю вміти розв’язувати такі рівняння з параметрами при написанні ДПА та ЗНО з математики.
Мета даної роботи розповісти про розв’язування рівнянь з параметрами, пов'язаних із властивостями функцій.
Для досягнення поставленої мети необхідно вирішити такі завдання:
1) дати визначення поняттям параметр та рівняння з параметрами;
2) показати принцип розв’язання даних рівнянь на загальних випадках;
3) показати розв’язання рівняння з параметрами, пов'язаних із властивостями функцій.
Для виконання поставленої мети були використані наступні методи: використання літератури різного типу, робота в групах на уроках алгебри.
Об'єктом дослідницької роботи було розв’язання рівнянь з параметрами, пов'язаних із властивостями функцій.
- Теоретичні основи розв’язування рівнянь з параметрами
Вивченню теми «Рівняння з параметрами» у шкільній програмі не приділено достатньої уваги.
Більшість посібників адресовано абітурієнтам, однак починати знайомитися з подібними завданнями потрібно набагато раніше - паралельно з відповідними розділами шкільної програми з математики.
Так, наприклад з параметрами ми зустрічаємося під час вивчення таких понять:
-
Функція пряма пропорційність: у = kx (х і у – змінні; k – параметр, k
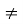 0);
0);
- Лінійна функція: у = kx + b (х і у – змінні; k і b – параметри);
- Лінійне рівняння: аx + b = 0 (х – змінна; а і b – параметри);
-
Рівняння першого степеня: аx + b = 0 (х – змінна; а і b – параметри; а
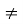 0);
0);
-
Квадратне рівняння: аx2 + bx + с = 0 (х – змінна; а , b і с – параметри; а
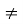 0);
0);
До задач з параметрами, які розглядаються в курсі середньої школи, можна віднести, наприклад, пошук розв’язків лінійних та квадратних рівнянь в загальному вигляді, дослідження кількості їх коренів в залежності від значень параметрів.
Природно, що такий невеликий клас задач багатьом учням не дозволяє усвідомити головне: параметр (фіксоване, але невідоме число) має двоїсту природу.
По-перше, параметр можна розглядати як число, а по-друге, - це невідоме число.
Таким чином, ділення на вираз, який містить параметр, добування кореня парного степеня із таких виразів потребує попередніх досліджень. Як правило, результати досліджень впливають і на розв’язок, і на відповідь.
Не випадково задачі з параметром є невід’ємним атрибутом завдань на ДПА з математики, а також зовнішнього незалежного оцінювання, оскільки вміння розв’язувати такі задачі свідчать, що учень має ґрунтовну математичну підготовку, високий рівень логічного мислення, навички дослідницької діяльності.
Незважаючи на те що програма з математики загальноосвітньої школи не передбачає формування в учнів умінь розв’язувати задачі з параметрами, реалії сьогодення (обовязкове ЗНО) диктують необхідність ознайомлення учнів із задачами з параметрами та методами їх розв’язування.
Головне, що треба засвоїти під час першого знайомства з параметром, - це необхідність обережного, навіть, якщо хочете, делікатного поводження з фіксованим, але невідомим числом. Цьому, на нашу думку, багато в чому будуть
сприяти наші приклади.
Необхідність акуратного поводження з параметром добре видно на тих прикладах, де заміна параметра числом робить задачу банальною. До таких задач, наприклад, належать: порівняти два числа, розв’язати лінійне або квадратне рівняння, нерівність і т.д.
Якщо в рівняння (нерівність, систему рівнянь, систему нерівностей) крім невідомих величин, входять числа, що позначені буквами, які не вказані, але вважаються відомими та заданими на деякій числовій множині, то вони називаються параметрами.
Якщо рівняння (нерівність, систему рівнянь, систему нерівностей) містить параметр і треба знайти його корені (розв’язки) залежно від параметра, то таке завдання відносять до задач із параметрами.
Існують завдання, в яких треба знайти всі значення параметра, при яких корені рівняння (розв’язки нерівності або системи) задовольняють певну умову. Такі завдання теж вважають задачами з параметрами. У деяких посібниках ці задачі ще називають «дослідницькі задачі з параметрами».
Розв’язати рівняння (нерівність, систему рівнянь, систему нерівностей) з параметрами означає знайти всі розв’язки для кожної системи допустимих значень параметрів.
Під час розв'язування задач із параметрами область зміни параметрів може бути заданою.
Якщо не вказані межі зміни параметрів, то вважається, що параметри набувають усіх своїх допустимих значень.
Наприклад ,у рівнянні ах -5 =7, х – змінна величина, яку треба знайти залежно від параметра, а, перетворивши це рівняння, дістанемо: ах = 12. Отже, при а ≠ 0 х =![]() ; при а = 0 рівняння коренів немає.
; при а = 0 рівняння коренів немає.
- Лінійні рівняння ах +b = 0, де х – змінна, а, b – числа.
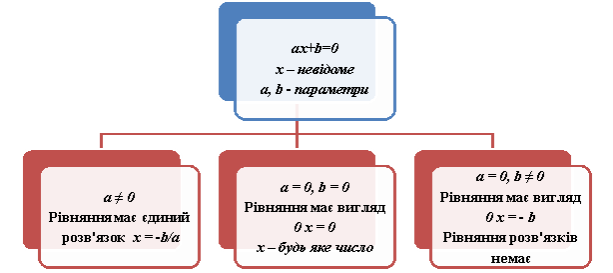
Приклад 1. Розв'язати рівняння а2х - 1= х+а
Розв’язання.
![]() Виконавши у рівнянні а2х - 1= х+а тотожні перетворення, дістанемо: ( а2 - 1 ) х = а + 1.
Виконавши у рівнянні а2х - 1= х+а тотожні перетворення, дістанемо: ( а2 - 1 ) х = а + 1.
-
якщо а2 – 1≠0, то х =
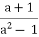 , тобто
, тобто 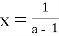 ;
;
-
якщо а2 – 1=0, то а =
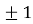 і можливі два випадки:
і можливі два випадки:
- якщо а = - 1, то рівняння матиме вигляд 0х = 0, тобто коренями рівняння є всі числа;
- якщо а = 1, то рівняння матиме вигляд 0х = 2, така рівність неможлива, тому рівняння коренів не має.
Відповідь: При а ≠![]() х =
х = ![]() ; при а = - 1 коренями рівняння є всі числа; при а = 1 рівняння коренів не має.
; при а = - 1 коренями рівняння є всі числа; при а = 1 рівняння коренів не має.
Приклад 2. Розв’язати рівняння ах -3 = b залежно від параметрів а і b.
Розв’язання.
Виконавши у рівнянні ах-3 = b тотожні перетворення, дістанемо: ах = b+3.
1) якщо а≠0, то х = ![]() при будь – якому b;
при будь – якому b;
2) якщо а =0, то при b= -3 рівняння набуває вигляду 0х=0, тобто коренями рівняння є всі числа;
3) якщо а=0 і b≠-3, отримаємо 0х = b +3 ≠0, така рівність неможлива, тому рівняння коренів не має.
Відповідь: При а ≠0 і будь – якому b х =![]() ; при а =0 і b = -3 корені рівняння – всі числа; при а=0 і b≠0 коренів немає.
; при а =0 і b = -3 корені рівняння – всі числа; при а=0 і b≠0 коренів немає.
-
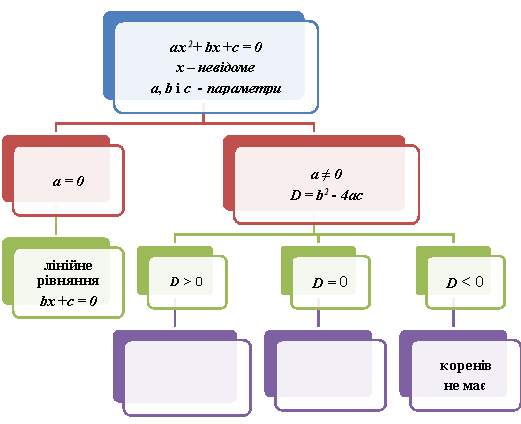 Квадратні ах 2+ bх +с= 0, де х – змінна, а, b, с – числа, причому а ≠0
Квадратні ах 2+ bх +с= 0, де х – змінна, а, b, с – числа, причому а ≠0
![]()
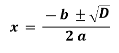
Приклад 3. Розв'язати рівняння (а+1)х2+2ах+а-2=0
Розв’язання.
Якщо а = -1, то рівняння матиме вигляд -2х – 3 = 0. Звідси, х = -1,5.
Якщо а ![]() -1, то D = 4а2-4(а+1)(а-2) = 4(а+2).
-1, то D = 4а2-4(а+1)(а-2) = 4(а+2).
- Якщо D = 0, тобто а = -2, то х1 = х2 = -2.
![]()
- Якщо D > 0, тобто а > -2, то
-
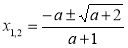 Якщо D < 0, тобто а < -2, то рівняння коренів не має.
Якщо D < 0, тобто а < -2, то рівняння коренів не має.
Відповідь: При а = -1 х = -1,5; при а = -2 х = -2; при а > -2 ;
при а < -2 рівняння коренів не має.
Приклад 4. При якому найменшому цілому значенні параметра m корені рівняння 3х2 – (4т + 1)х – т – 2 = 0 містяться у проміжку ![]() ?
?
Розв’язання.
Спочатку знайдемо значення т, при яких корені є у відкритому проміжку (-2;1), а кінцеві точки розглянемо окремо.
![]()
![]() D = (4т + 1)2 - 4∙3∙(-2) = 16т2 + 20т + 25>0 при будь – якому т
D = (4т + 1)2 - 4∙3∙(-2) = 16т2 + 20т + 25>0 при будь – якому т![]() , то рівняння має два різні корені.
, то рівняння має два різні корені.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тоді т визначається з системи нерівностей 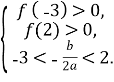 ,
,
де f(x) = 3х2 – (4т + 1)х – (т + 2).
Розв’язавши її , знайдемо, що т![]()
![]() .
.
Розглянемо тепер кінцеві точки проміжку ![]() . Якщо f(-3)= 0, то т =
. Якщо f(-3)= 0, то т = ![]() і х1 = - 3, х2 =
і х1 = - 3, х2 = ![]() , що задовольняє умову задачі.
, що задовольняє умову задачі.
Якщо f(2)= 0, то т = ![]() і х1 = 2, х2 =
і х1 = 2, х2 = ![]() , що також підходить.
, що також підходить.
Отже, тє ![]() .
.![]()
Відповідь: т = - 2.
- Дробово - раціональні рівняння
Дробово – раціональне рівняння замінюється цілим рівнянням шляхом тотожних перетворень. Після цього розв’язується ціле рівняння, виключаючи сторонні корені . У випадку рівнянь з параметрами це завдання більш складне. Тут, щоб сторонні корені виключити, потрібно знаходити значення параметра, що перетворює загальний знаменник в нуль, тобто розв’язувати відповідні рівняння щодо параметра.
Приклад 5. Розв’язати рівняння ![]()
Розв’язання.
Якщо а = 0, то рівняння не має змісту і отже, не має коренів.
Якщо а ![]() 0, о дане рівняння рівносильне системі
0, о дане рівняння рівносильне системі
![]()
Розв’яжемо перше рівняння системи:
![]()
D = 4(1-а)2 – 4(а2 – 2а-3) = 16;
х1 = а + 1; х2 = а - 3;
Враховуючи другу умову, маємо х![]() -1; х
-1; х![]() -2. Отже, а
-2. Отже, а![]() -2; а
-2; а![]() -3, а
-3, а![]() 1, а
1, а![]() 2.
2.
Таким чином, при а = -2 х1 = а + 1= -1 – сторонній корінь;
х2 = а -3 = -5.
При а = -3 х1 = а + 1= -2 – сторонній корінь;
х2 = а -3 = - 6.
При а = 1 х1 = а + 1= 2;
х2 = а -3 = - 2 – сторонній корінь.
При а = 2 х1 = а - 3= -1– сторонній корінь;
х2 = а + 1 = 3.
Відповідь: Якщо а = - 3, то х = - 6; якщо а = - 2, то х = - 5; якщо а = 0, то коренів не має; якщо а = 1, то х = 2; якщо а = 2, то х = 3; якщо а ![]() -3, а
-3, а ![]() -2;
-2;
а ![]() 0; а
0; а ![]() 1; а
1; а ![]() 2, то х1 = а + 1; х2 = а +2.
2, то х1 = а + 1; х2 = а +2.
Приклад 6. Визначити суму значень параметра с, при яких рівняння ![]() не має розв’язку.
не має розв’язку.
Розв’язання.
Дане рівняння рівносильне рівнянню х∙(1 – 2с) + 1 – 2с2 = 0, х ![]() - с.
- с.
х (1 – 2с) = - 1 + 2с2. Отримане лінійне рівняння не має коренів, якщо
![]()
с = 0,5; с ![]()
![]() .
.
Перевіркою встановлюємо, що при с = 1 рівняння ![]() не має змісту.
не має змісту.
Тому рівняння не має розв’язку при с = 0,5 і с = 1. Сума параметрів 1,5.
Відповідь: 1,5.
- Ірраціональні рівняння
Головними особливостями при розв’язуванні рівнянь такого типу є:
- обмеження області визначення невідомої х, так як вона змінюється в залежності від значення параметра;
-
у розв’язування рівнянь виду
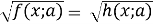 при піднесенні в квадрат потрібно враховувати знак h(x;a) і проводити перевірку коренів.
при піднесенні в квадрат потрібно враховувати знак h(x;a) і проводити перевірку коренів.
Приклад 7. (ЗНО 2012, 1 сесія, завдання 32)
При якому найменшому цілому значенні а рівняння
![]() має лише два різні корені?
має лише два різні корені?
Розв’язання.
ОДЗ: 2х + 15 ≥ 0; х ≥ -7,5.
![]() =0;
=0;
![]() = 0;
= 0;
![]() = 0;
= 0;
![]() = 0;
= 0;
![]() = 0 або
= 0 або ![]() ;
;
![]()
Якщо х ≥ 5, то х + 9 – х + 5 – а = 0; а = 14 для будь – яких значень х отримали безліч розв’язків, що не задовольняє умову.
Якщо -7,5 ≤ х < 5, то х + 9 + х - 5 – а = 0; х = ![]() .
.
х ≥ -7,5, але корені різні, то х = ![]() > 7,5. Отже а > -11. Найменше ціле значення а = -10.
> 7,5. Отже а > -11. Найменше ціле значення а = -10.
Відповідь: а = -10.
Приклад 8. (ЗНО 2012, 2 сесія, завдання 32) При якому найменшому значенні а рівняння ![]() має хоча б один корінь?
має хоча б один корінь?
Розв’язання.
ОДЗ: х – 3 ≥ 0; х ≥ 3.
Виконаємо перетворення:![]()
![]() .
.
Рівняння матиме вигляд : ![]() .
.
Введемо нову змінну: ![]() = t, t ≥ 0.
= t, t ≥ 0.
t2+(14-2a) t + 33 – 6a = 0;
D = 4 (a – 4)2;
Якщо D = 0, то 4 (a – 4)2=0; а = 4
t = ![]() - сторонній корінь.
- сторонній корінь.
D > 0, то (а – 4)2 > 0; а є (-∞; 4) U (4; ∞).
t1,2= а – 7 ± ![]() = а - 7±
= а - 7± ![]()
а > 4, то t1 = а – 7 + 4 – а = - 3 – сторонній корінь;
t2 = а – 7 - 4 + а = 2а – 11 ≥ 0, то а ≥ 5,5.
а < 4, то t1 = а – 7 + 4 – а = - 3 – сторонній корінь;
t2 = а – 7 - 4 + а = 2а – 11 ≥ 0, то а ≥ 5,5.
Найменше значення параметра а = 5,5.
Відповідь: а = 5,5.
Приклад 9. (ЗНО 2013, 2 сесія, завдання 33)
При якому найбільшому від’ємному значенні параметра а рівняння ![]() - 2х = а має один корінь?
- 2х = а має один корінь?
Розв’язання.
ОДЗ: ![]() ≥ 0, х є (-∞; -1]U[1; ∞).
≥ 0, х є (-∞; -1]U[1; ∞).
Так як значення параметра а за умовою повинно бути від’ємним, то ![]() - 2х < 0, але
- 2х < 0, але ![]() ≥ 0 завжди, отже 2х >
≥ 0 завжди, отже 2х > ![]() > 0, тобто х > 0 .
> 0, тобто х > 0 .
![]() , якщо х > 0, то дане рівняння рівносильне рівнянню
, якщо х > 0, то дане рівняння рівносильне рівнянню ![]() - 2х = а.
- 2х = а.
І спосіб
Розглянемо функцію у = ![]() - 2х. Найбільше від’ємне значення параметра а є найбільшим значенням функції, для знаходження якого потрібно знайти критичні точки.
- 2х. Найбільше від’ємне значення параметра а є найбільшим значенням функції, для знаходження якого потрібно знайти критичні точки.
![]() = 0;
= 0; ![]() = 8;
= 8; ![]() ;
; ![]() ; х =1,0625.
; х =1,0625.
Для того, щоб показати, що критична точка є точкою максимуму, треба показати, що похідна функції змінює знак з «+» на «_» при переході через цю точку зліва направо. Візьмемо х = 1,0001 (1 < 1,0001 < 1,0625)
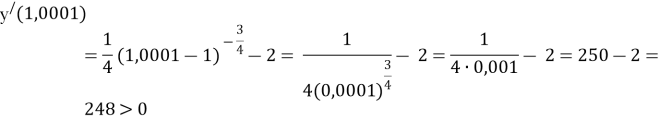
Візьмемо х = 2, 2 > 1,0625
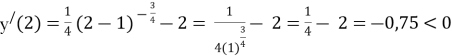 .
.
Отже, хтах = 1,0625.
утах = ![]() - 2∙ 1,0625 = 0,5 – 2,125 = - 1,625. Отже а = - 1,625
- 2∙ 1,0625 = 0,5 – 2,125 = - 1,625. Отже а = - 1,625
Відповідь: а = - 1,625.
ІІ спосіб
Запишемо рівняння ![]() - 2х = а у вигляді
- 2х = а у вигляді ![]() = 2х + а. Розв’яжемо рівняння графічно. Дане рівняння матиме один корінь, якщо графіки функцій у =
= 2х + а. Розв’яжемо рівняння графічно. Дане рівняння матиме один корінь, якщо графіки функцій у = ![]() і у = 2х + а матимуть одну точку перетину, тобто пряма у = 2х + а буде дотичною до кривої у =
і у = 2х + а матимуть одну точку перетину, тобто пряма у = 2х + а буде дотичною до кривої у = ![]() . Виходячи з геометричного змісту похідної, отримаємо k = f /(x0 ) = 2.
. Виходячи з геометричного змісту похідної, отримаємо k = f /(x0 ) = 2.
![]() ; Отже:
; Отже: ![]() ;
; ![]()
![]()
![]() = 1,0625; у0 =
= 1,0625; у0 = ![]() =
= ![]() = 0,5.
= 0,5.
![]() - точка дотику. Підставимо її координати у рівняння прямої у = 2х + а. Матимемо: 2∙ 1,0625 + а = 0,5; а = -1,625.
- точка дотику. Підставимо її координати у рівняння прямої у = 2х + а. Матимемо: 2∙ 1,0625 + а = 0,5; а = -1,625.
Відповідь: а = - 1,625.
- Показникові рівняння
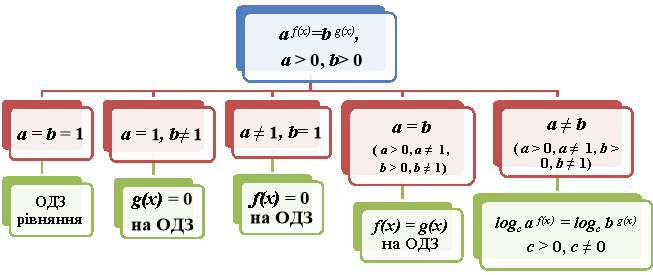
Більшість показникових рівнянь з параметром зводяться до показникових рівнянь виду а f(x)=b g(x), a > 0, b> 0.
Область допустимих значень такого рівняння знаходиться як перетин областей допустимих значень функцій f(x) і g(x). Для розв’язання рівняння потрібно розглянути такі випадки:
- при а = b = 1 розв’язком рівняння є область його допустимих значень D;
-
при а = 1, b
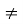 1 розв’язком рівняння є корені рівняння g(x) = 0 на області допустимих значень D;
1 розв’язком рівняння є корені рівняння g(x) = 0 на області допустимих значень D;
-
при а
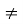 1, b = 1 розв’язком рівняння є корені рівняння f(x) = 0 на області допустимих значень D;
1, b = 1 розв’язком рівняння є корені рівняння f(x) = 0 на області допустимих значень D;
-
при а = b ( а > 0, а
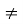 1, b > 0, b
1, b > 0, b 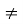 1) рівняння тотожне рівнянню f(x) = g(x) на області допустимих значень D;
1) рівняння тотожне рівнянню f(x) = g(x) на області допустимих значень D;
-
при а
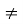 b ( а > 0, а
b ( а > 0, а 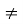 1, b > 0, b
1, b > 0, b 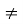 1) рівняння тотожне рівнянню
1) рівняння тотожне рівнянню 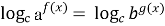 (c > 0, с
(c > 0, с 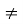 1) на області D.
1) на області D.
Приклад 10. При яких значеннях параметра а рівняння 4 х – (а + 1)∙ 2 х + 2а – 2 = 0 має два різних корені?
Розв’язання.
Нехай 2 х = t, t ≥ 0. Маємо: t 2 – (а + 1)∙ t + 2а – 2 = 0.
D = (а – 3)2
Звідси t 1 = 2; t 2 = а – 1. Отже, початкове рівняння рівносильне сукупності: 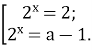
Перше рівняння сукупності має єдиний корінь х = 1.
Друге рівняння сукупності при кожному значенні параметра а або має один корінь, або взагалі не має коренів.
Для виконання умови задачі друге рівняння повинно мати єдиний корінь, який не дорівнює 1 (бо корені повинні бути різними).
Якщо х ≠ 1, то ![]() , то а ≠ 3.
, то а ≠ 3.
Рівняння ![]() має корінь, якщо
має корінь, якщо ![]() . Тобто при а > 1 і а ≠ 3 рівняння 4 х – (а + 1)∙ 2 х + 2а – 2 = 0 має два різних корені.
. Тобто при а > 1 і а ≠ 3 рівняння 4 х – (а + 1)∙ 2 х + 2а – 2 = 0 має два різних корені.
Відповідь: а є (1; 3)U(3; ∞)
Приклад 11. Розв’язати рівняння а х+1=2 3- х
Розв’язання. ОДЗ : хє R; a > 0
- Якщо a ≤ 0, то рівняння не має змісту;
- Якщо а = 2, то 2 3- х= 2 х + 1; х + 1 = 3 – х, х = 1
-
При
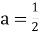 , отримаємо рівняння
, отримаємо рівняння
2– ( х +1) = 2 3 - х, тобто рівняння – х – 1 = 3 – х, що не має коренів.
-
При а
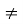 2 і а
2 і а 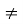
 ( а > 0) прологарифмуємо вихідне рівняння за основою а і отримаємо:
( а > 0) прологарифмуємо вихідне рівняння за основою а і отримаємо:
![]() ;
;
![]() ;
;
х = ![]() .
.
Відповідь: При a ≤ 0 або ![]() розв’язків не має; при а = 2 х = 1; при а
розв’язків не має; при а = 2 х = 1; при а ![]() 2 і а
2 і а ![]()
![]() ( а > 0) х =
( а > 0) х = ![]() .
.
- Тригонометричні рівняння
Більшість тригонометричних рівнянь з параметрами зводиться до розв’язування найпростіших тригонометричних рівнянь трьох типів, причому необхідно враховувати обмеженість тригонометричних функцій у = sin x і y = cos x.
Приклад 12. Знайдіть усі цілі значення параметра к, при яких рівняння ![]() має дійсні корені. Знайдіть ці корені.
має дійсні корені. Знайдіть ці корені.
Розв’язання:
Перетворимо праву частину: 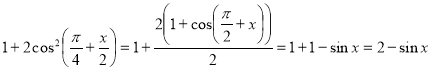
Розв’яжемо тригонометричне рівняння:
![]()
![]()
Так як ![]() , то дана рівність можлива лише у випадку, коли кожний з доданків дорівнює 1, тому одержимо сукупність рівнянь:
, то дана рівність можлива лише у випадку, коли кожний з доданків дорівнює 1, тому одержимо сукупність рівнянь:
![]() ;
; 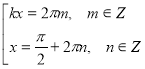 ;
; 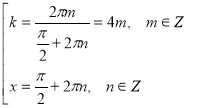
Відповідь: ![]()
Приклад 13. (ЗНО 2011, завдання 35)
Знайти найменше значення а, при якому має розв’язки рівняння ![]() .
.
Розв’язання.
Перетворимо праву частину:![]()
![]()
![]()
Так як -1 ≤ ![]() ≤ 1, то -1 ≤
≤ 1, то -1 ≤ ![]() ≤ 1. Дана нерівність рівносильна системі нерівностей:
≤ 1. Дана нерівність рівносильна системі нерівностей: 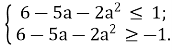
Розв’яжемо першу нерівність системи: ![]() ;
; ![]()
D=81; ![]() ; а1 = -3,5, а2 = 1.
; а1 = -3,5, а2 = 1.
![]()



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
а![]() [-3,5; 1]
[-3,5; 1]
Розв’яжемо другу нерівність системи:![]() ;
; ![]()
![]() D=65;
D=65; ![]() ; а1 =
; а1 = ![]() , а2 =
, а2 = ![]() .
.
![]()
![]()
![]()


![]()
![]()
![]()
![]()
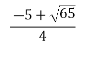
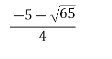
а![]() (-∞;
(-∞;![]() ]U[
]U[![]() ; ∞)
; ∞)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а
а![]() [-3,5;
[-3,5;![]() ]U[
]U[![]() ; 1]; а тіп = -3,5
; 1]; а тіп = -3,5
Відповідь: а тіп = -3,5.
- Логарифмічні рівняння
Розв’язування логарифмічних рівнянь з параметрами зводиться до пошуку коренів елементарного логарифмічного рівняння. Важливим моментом розв’язування рівнянь подібного типу є перевірка приналежності знайдених коренів ОДЗ вихідного рівняння.
Сформулюємо декілька заповідей, які необхідно засвоїти всім бажаючим навчитися розв’язувати задачі з даної теми.
Ось ці «заповіді»:
1. Вміти розв’язувати звичайні логарифмічні рівняння.
2. Розпочинати розв’язання з формулювання області визначення виразу.
3. Мати на увазі, що ![]() і
і ![]() ; при умові b∙c > 0
; при умові b∙c > 0![]() і
і ![]()
4. Не забувати про графічні засоби розв’язання задач.
5. Окремо досліджувати граничні значення параметрів – це дозволить
проконтролювати роботу.
Приклад 14. Знайти всі значення параметра а, при яких рівняння lg 2 (1 + х 2) + (3а - 2) ∙ lg (1 + х 2) + а 2 = 0 не має коренів.
Розв’язання.
Позначимо lg (1 + х 2) = t, тоді вихідне рівняння матиме вигляд:
t 2 + (3а - 2) ∙t + а 2 = 0.
Це рівняння - квадратне з дискримінантом
D = (3а - 2) 2 - 4а 2 = 5а 2 - 12а + 4.
Якщо D < 0 , тобто при 5а 2 - 12а + 4 <0 рівняння коренів не має .
5а 2 - 12а + 4 <0
а 1 = 0,4; а 2 =2
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0,4 < а <2.
Відповідь: (0,4; 2)
Приклад 15. (ЗНО 2013, 1 сесія, завдання 33)
Знайдіть значення параметра а, при якому корінь рівняння ![]() належить проміжку (1;1,5).
належить проміжку (1;1,5).
Розв’язання.
![]() ≥ 0 , то
≥ 0 , то ![]() ≥ 0 або
≥ 0 або ![]() .
.
Але -1 ≤ ![]() ≤ 1, то
≤ 1, то ![]() Тоді
Тоді ![]() , а отже
, а отже
![]() .
.
Розв’яжемо ![]()
![]() ;
;
![]()
За умовою х![]() (1; 1,5), то при п = 3 х = 1,3
(1; 1,5), то при п = 3 х = 1,3![]() (1; 1,5).
(1; 1,5).
Розв’яжемо ![]() ; 16 + а – х = 0; а = х – 16;
; 16 + а – х = 0; а = х – 16;
При х = 1,3 а = 1,3 – 16 = - 14,7.
Відповідь: а = - 14,7.
Висновок
- В роботі були розглянуті методи розв'язування рівнянь з параметрами, як стандартними, так і нестандартними методами
- Серед методів розв'язання рівнянь з параметрами використовують як аналітичні (із використанням формул, властивостей функцій) так і графічні.
- Для того, щоб набути міцних та глибоких знань, оволодіти способами і методами розв’язування рівнянь з параметрами, дуже важливо розв’язати їх достатню кількість, щоб систематизувати та узагальнити знання по даній темі.
- Матеріал даної роботи сприяє систематизації, поглибленню і розширенню знань, навичок та умінь розв’язувати рівняння з параметрами та їх цілеспрямованому використанні під час виконання різних типів завдань.
- Ця тема повинна вивчатися не тільки на факультативах і додаткових заняттях, але й у шкільній програмі, тому що вона формує логічне мислення й математичну культуру в школярів. Учням знання з цієї теми допоможуть здати ДПА і ЗНО.
Список використаної літератури
1. Дорофеев Г.В., Решение задач, содержащих параметры / Дорофеев Г.В - М.: Перспектива, 2000. - Ч.2. - 38 с.
2. Глаголєва Н.Ю., Задачі по математиці для вступників у вузи./ Глаголєва Н.Ю - К., 2009р. - 274 с.
3. Горнштейн П.І., Задачі з параметрами./ Горнштейн П.І., Полонский В.Б., Якір М.С.- К., 2006 р. - 150 с.
4. Лікоть В.В., Задачі з параметрами./ Лікоть В.В - К., 2007р. - 54 с.
5. Мордкович А.Г., Алгебра й початок аналізу/ Мордкович А.Г. - К., 2008 р. - 256 с.
6. Никонов Е.Ю., Параметр. / Никонов Е.Ю. - Самара - 1998 р. - 80 с.
7. Новосьолов С.І., Спеціальний курс елементарної алгебри./ Новосьолов С.І Москва-1997. -120 с.
8. Ткачук В.В., Математика - абітурієнтові./ Ткачук В.В., - К., 1994р. -56с.
9. Ципкін А.Г., Справочник по методам решения задач по математике для средней школы / Ципкін А.Г., Пінський А.І - 2-е вид.. перероб. і доп. - М.: Наука, 2004. - 576 с.
10. Харитонова Л.О. Параметри // Математика в шк. України./ Харитонова Л. О. - 2008. - № 29. - С. 27-30.
11. Ястребинецкий Г.А., Задачи с параметрами / Ястребинецкий Г.А - М.: Просвещение, 1999. - 128 с.
12. Ястребинецький Г.А. Рівняння й нерівності, що містять параметри./ Ястребинецкий Г.А - К., 2005р. - 208 с.
1


про публікацію авторської розробки
Додати розробку
