Різниця квадратів. (Добуток різниці двох виразів на їх суму)

Тема. Різниця квадратів. (Добуток різниці двох виразів на їх суму)

Мета: (шляхом виконання випереджального домашнього завдання) індуктивним методом вивести формулу, відому як різниця квадратів двох виразів, і таким чином домогтися свідомого розуміння учнями змісту цієї формули; здійснити первинне закріплення формули; виробити вміння за­писувати, читати та застосовувати формулу

(a – b)(a + b) = a² – b² для пере­творення виразів у многочлен стандартного вигляду.

Тип уроку: засвоєння знань.

Хід уроку

I. Організаційний момент

 Учитель спонукає учнів до перевірки готовності до уроку, фіксує прізвища відсутніх.

II. Перевірка домашнього завдання

 Одна з можливих форм перевірки № 1 домашнього завдання — організація самоперевірки, коли учні дістають правильні розв'язання у вигляді індивідуальних карток-ксерокопій або як записи на дошці (ксерокопії — кращий варіант, бо економимо час) і звіряють самостійно свої розв'язки з розданими. У разі необхідності учні формулюють питання, відповіді на які дає або вчитель, або учні-консультанти (роботу яких можна потім оцінити).

III. Формулювання мети й завдань уроку

 Після перевірки домашнього завдання (№ 1 та № 2) учням нага­дуємо (або пропонуємо усвідомити самим і сформулювати думку), що, вивчаючи тему «Многочлени», ми серед інших, навчилися ви­конувати таку дію, як множення двох многочленів. Причому на попередніх двох уроках ми з'ясували, що в деяких окремих випадках цю дію можна виконувати «скорочено» за відповідними формулами скороченого множення. На уроці ми познайомимося ще з однією формулою, яку називають «різниця квадратів».

IV. Робота з випереджальним домашнім завданням

 Запитання учням для самостійного опрацювання.

1. Що таке многочлен? члени многочлена? подібні члени многочлена?
2. Який многочлен називають многочленом стандартного вигляду?
3. Як помножити одночлен на многочлен? многочлен на многочлен?
4. За алгоритмом множення двох многочленів виконати множення даних многочленів та звести утворені вирази до многочлена стандартного ви­гляду: 1) (x – y)(x + y); 2) (a – b)(a + b); 3) (c – d)(c + d); 4) (m – n)(m + n).
5. Прочитайте ліву та праву частину утворених рівностей, використовую­чи слова «добуток», «сума», «різниця». Порівняйте прочитані вирази.
6. Сформулюйте висновки.

Після проведення роботи учні презентують свої відповіді й коригують виконані завдання. Мета цієї роботи: усвідомлення факту, що добуток різниці будь-яких двох виразів на їх суму є різницею квадратів цих двох виразів.

V. Засвоєння знань

 Після виконаної роботи з випереджальним домашнім завданням учителю залишається лише узагальнити сформульовані умовиводи учнів та скласти відповідний алгоритм. Дуже важливо (як і під час вивчення інших формул скороченого множення), щоб учні усвідомили, що у запису

(a – b) (a + b) = a² – b²

a i b — будь-які вирази (числа, одночлени і навіть многочлени) і знання формули включає в першу чергу словесне її формулювання.

У зошитах учні можуть виконати такий запис:

Виконання усних вправ

1. Прочитайте вираз:

(a + 8)²; а² + 8²; (0,2x – 4)²; (0,2x)² – 4²; x² + 4; x² – у².

2. Піднесіть до квадрата вираз: 2; 2b; 2b²; 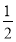b².
3. Вкажіть правильну рівність:

1) (a – 2b)(a + 2b) = (a – 2b)²;     2) (a – 2b)(a + 2b) = a² – 2b²;

3) (a – 2b)(a + 2b) = a² + 4b²;     4) (a – 2b)(a + 2b) = a² – 4b².

Виконання письмових вправ

1. Подайте у вигляді многочлена вираз:

1) (х – у)(х + у);  2) (р + q)(р – q);   3) (b – а)(b + а);

4) (р – 7)(р + 7),  5) (2х – 1)(2х + 1);  6) (п – 3т)(3т + п);

7) (2а – 3b)(3b + 2а);  8) (10x – 7y)(10x + 7y).

2. Виконайте множення:

1) (х² – 5)(х² + 5);   2) (а² + 3)(а² – 3);

3) (а³ – b²)(а³ + b²);  4) (5х² – 2у²)(5х² + 2у²).

 Під час виконання цих вправ важливо вимагати від учнів прочитати як умову, так і здобутий результат (це забезпечує більш усвідомлене застосування формули). У роботі з формулою на початковому етапі необхідно підкреслювати, що у формулюванні записується спочат­ку різниця (відпрацьовуючи практичні навички, треба дотримува­тись принципу переходу від «простого до складного», і цей перехід треба здійснювати поступово, переконавшись у сформованості на­вичок застосування співвідношення в більш простій ситуації).

3. Подайте у вигляді многочлена:

1) 2(х – 3)(х + 3); 2) у(у + 4)(у – 4); 3) 5х(х + 2)(х – 2); 4)(3 – у)(3 + у)(9 + у²).

4. Спростіть вираз:

1) 2х² – (х + 1)(х – 1);   2) (3аb – 1)(3аb + 1) – 8а²b²;

3) (х – 2)(х + 2) – х(х + 5); 4) 2а(а + b) – (2а + b)(2а – b);

5) (3m – n)(3m + n) – (2m + n)(2m – n);

6) (5a – 3c)(5a + 3c) – (7c – a)(7c + a).

 Якщо вистачить часу, можна запропонувати вправу на спрощення обчислень за рахунок застосування формул.

5. Виконайте обчислення:

1) (100 – 1)(100 + 1); 2) (80 + 3)(80 – 3); 3) 74 ∙ 66;

4) 201 ∙ 199; 5) 1002 ∙ 998;  6)1,05 ∙ 0,95.

VII. Підсумки уроку

Експрес-контроль

1. Заповніть пропуски у твердженні:

Добуток... двох виразів на їх суму... різниці... цих виразів.

2. Який із записів правильний?

1) (х – 3у)(х + 3у) = х² – 3у²;  2) (х – 3у)(х + 3у) = (х – 3у)²;

3) (х – 3у)(х + 3у) = х² + 9у²;  4) (х – 3у)(х + 3у) = х² – 9у².

VIII. Домашнє завдання

Використовуючи формулу різниці квадратів, виконайте завдання.

№ 1. Подайте вираз у вигляді многочлена:

1) (a + 5)(a – 5); 2) (4 + x)(4 – x); 3) (2a – 7)(2а + 7); 4) (12x + 13у)(12x – 13y);

5) (а³ – b⁴)(a³ + b⁴); 6) .

№ 2. Спростіть вираз:

1) (4х – 3у)(4х + 3у) + (3х + 4у)(4у – 3х); 2) (х + 2)² – (х – 3)(х + 3);

3) (у – 2)(у + 3) – (у – 1)² + (5 – у)(у + 5).

№ 3. Випереджальне домашнє завдання. За довідником (5-6 клас) повторіть:

1.   Який закон множення використовується при множенні трьох і біль­ше множників?
2.   Як зміниться добуток двох виразів, якщо змінити знак одного множ­ника? обох множників?
3.   Яким стане вираз, якщо змінити його знак на протилежний? (Як це зробити?) а; (-а + b); (-а – b), (-c – d + a); (-1 + d – a).