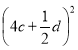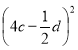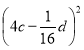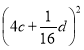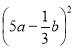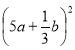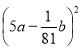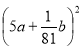Використання формул скороченого множення для розкладання многочленів на множники

Тема. Використання формул скороченого множення для розкладання многочленів на множники

Мета: виробити в учнів уміння розкладати різницю квадратів та суму й різницю кубів на множники із використанням відповідних формул ско­роченого множення.

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

I. Організаційний момент

Учитель спонукає учнів до само- та взаємоперевірки готовності до уроку; перевіряє наявність учнів на уроці.

II. Перевірка домашнього завдання

 Ступінь засвоєння навичок і вмінь, опрацьованих на попередньому уроці, можна перевірити під час виконання тестового завдання.

По закінченні цієї роботи здійснюємо самоперевірку та корекцію, по­вторивши основні теоретичні положення.

III. Формулювання мети й завдань уроку

 Після проведеного II етапу уроку, під час якого повторюються основні теоретичні відомості, використані на попередньому уроці, більшість учнів усвідомлює той факт, що основною метою уроку буде подальша робота з вироблення вмінь та відпрацювання нави­чок використання в подібних ситуаціях (розкладанні на множники) інших вивчених формул скороченого множення.

IV. Актуалізація опорних знань

Робота з випереджальним домашнім завданням

Виконання усних вправ

1. Подайте вираз у вигляді квадрата одночлена:

36;   l6у²;   0,09t²;   a²t²;  a⁸;   0,04b⁴.

2. Подайте вираз у вигляді куба одночлена:

27;   8х³;  m³п³;   0,064b⁴;   a¹²;   343а⁶b¹⁵.

3. Чому дорівнює неповний квадрат суми та неповний квадрат різниці виразів: х та у; 3 та х; а та 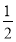; а² та 1?
4. Прочитайте вираз, використовуючи слова «сума», «різниця», «квадрат», «куб», «добуток»: a + b; a – b; a² – b²; a² + b²; а³ + b³; а³ – b³.

Які з цих виразів можна розкласти на множники за формулами скороче­ного множення? Прочитайте ці формули, використовуючи виділені слова.

V. Застосування вмінь

 Ця група формул (різниця квадратів та сума й різниця кубів) є більш простою для учнів. Але є кілька моментів, на які відразу слід зверну­ти увагу, щоб попередити можливі помилки:

1. щодо різниці квадратів: за формулою розкладається різниця квад­ратів і в жодному разі не сума (маємо на увазі тільки множину дійсних чисел); щоб застосувати цю формулу, даний вираз спочатку подаємо як різницю квадратів;
2. щодо суми/різниці кубів ще раз звертаємо увагу на запис та стежимо, щоб другий множник був саме неповним квадратом різниці/суми.

Виконання усних вправ

1. Подайте вираз у вигляді різниці квадратів двох виразів:

1) р² – 4; 2) 16 – с²; 3) b² – 1; 4) 4х² – 25; 5) 49а² – 9b²; 6) (т – 1)² – 4.

2. Подайте вираз у вигляді суми/різниці кубів двох виразів:

1) а³ – 1; 2) а³ – 8; 3) а⁶ – 1; 4) а³ – 0,027b³; 5) а⁶ – b¹².

3. Чи правильні рівності:

1) 4 – с² = (4 – c)(4 + c);   2) 16x² – т² = (4x² – т²)(4x² + m²);

3) 27 – а³ = (9 + а)(9 + 6а + а²);  4) 125 + b³ = (5 + b)(5 + 5а + а²)?

Виконання письмових вправ

1. Розкладіть на множники:

1) х² – 4; 2) 25 – 9а²; 3) 36т – 100п²; 4) 0,04р² – 1,69q²; 5) х²у² – ;

6) a⁴ – b⁶;  7) -1 + 49a⁴b⁸.

2. Розкладіть на множники за формулою різниці квадратів:

1) (х – 1)² – 49; 2) (3b – 5)² – 49; 3) (2х – 3)² – (х + 4)²; 4) а⁴ – (а – 7)².

3*. Розв'яжіть рівняння:

1) х² – 64 = 0; 2) 4х² – 25 = 0; 3) 9х² + 16 = 0; 4) (2х – 3)² – 36 = 0.

4. Розкладіть на множники:

1) т³ – п³; 2) с³ + 8; 3) 27а³ – b³; 4) 125 + а³b³; 5) х⁶ – у⁹;

6) 1000a¹²b³ + 0,001c⁹d¹⁵;  7*) (а + 7)³ – 8; 8*) (а – 12)³ + 27.

5*. Обчисліть значення виразу .

VI. Підсумки уроку

Встановіть відповідність

Поясніть вибір.

VII. Домашнє завдання

Повторити формули скороченого множення.

Використовуючи формули скороченого множення, виконати такі зав­дання.

№ 1. Розкладіть на множники:

1) 36х² – 169у²; 2) 0,09t⁴ – 121р²; 3) 1,69у¹⁴ – 900z⁸; 4) (4х – 3)² – 25х².

№ 2. (Розкладіть на множники). Подайте у вигляді добутку:

1) а³ + 64; 2) 0,008х³ – 0,027у³; 3) b⁹ + а¹²; 4) 343а⁶b¹⁵ – 0,008х⁹у³.

№ 3. Випереджальне домашнє завдання.

1) Замість □ підставте у вираз такий одночлен, щоб многочлен можна
було подати у вигляді квадрата двочлена:

х² + 2х + □; х² – 6х + □;  х² + 12х + □; х² – 5х + □.

2) Запишіть даний вираз у вигляді квадрата двочлена. Яких значень, ви­ходячи з цього, може набувати утворений (а отже, і даний) вираз? А якщо до нього додати додатне число а?

3) Подайте число у вигляді суми двох додатних чисел, одне з яких є (найближчим до нього) точним квадратом: 3; 5; 10; 51; 38; 90.