Сума та різниця кубів

Тема. Сума та різниця кубів

Мета: домогтися свідомого засвоєння змісту формул

(a ± b)(a² ab + b²) = a³ ± b³

та виробити базові вміння застосовувати ці формули для перетворень відпо­відних цілих виразів у многочлен стандартного вигляду.

Тип уроку: засвоєння знань.

Хід уроку

I. Організаційний момент

 Учитель перевіряє готовність учнів до уроку, налаштовує їх на ро­боту.

II. Перевірка домашнього завдання

 Щоб перевірити якість виконання домашнього завдання, збираємо зошити. Оскільки виконання вправ № 1-2 домашнього завдання передбачало використання як базових, так і вмінь більш високого рівня, вдало виконане домашнє завдання можна зарахувати як до­машню самостійну роботу (із виставленням оцінок до журналу).

III. Формулювання мети й завдань уроку

 Учитель знову нагадує учням (або спонукає їх до самостійної роботи щодо усвідомлення місця розділу, що вивчається: «Формули скоро­ченого множення» з теми «Многочлени та дії з ними») і формулює мету уроку: продовжити роботу з вивчення формул скороченого множення; виробити вміння застосовувати нові знання для пере­творення цілих виразів у многочлен стандартного вигляду.

IV. Актуалізація опорних знань

Виконання усних вправ

1. Прочитайте вираз:

1) (а – b); 2) (а + b); 3) (а – b)²; 4) (а + b)²; 5) а² – 2аb + b²; 6) а² + 2аb + b²;

7) а³ – b³; 8) а³ + b³; 9) а² – аb + b²; 10) а² + аb + b².

2. Подайте у вигляді многочлена:

(a + b)²; (a – b)²; (а + b)(а – b); (а + b)(с + d).

V. Вивчення нового матеріалу

1. Робота з випереджальним домашнім завданням.

Завдання 1. Використовуючи правило множення многочлена на мно­гочлен, виконайте множення многочленів. Утворені вирази (многочлени) зведіть до стандартного вигляду:

1) (а – b)(а² + аb + b²); 2) (а + b)(а² – аb + b²); 3) (с – d)(с² + сd + d²);

4) (с + d)(с² – сd + d²);  5) (т – 1)(т² + т + 1); 6) (т + 1)(т² – т + 1).

Завдання 2. Випишіть умову кожного із завдань та многочлен стандарт­ного вигляду, що йому тотожно дорівнює, і запишіть відповідні рівності.

Прочитайте ці рівності, використовуючи терміни «сума», «добуток», «різниця», «квадрат».

Порівняйте утворені рівності та зробіть висновок.

2. Засвоєння знань.

 Після виконаної роботи (див. п. 1) традиційно вчитель разом з учня­ми формулює спочатку у вигляді тотожності, а потім за допомогою слів формули, які мають назву «сума та різниця кубів» (двох виразів). У конспектах учні можуть зробити відповідні записи.

При цьому слід звернути увагу, що виділені слова допомагають краще запам'ятати зміст формул (бо часто учні, не задумуючись над змістом, припускаються в цих місцях помилок).

VI. Засвоєння вмінь

Виконання усних вправ

1. Назвіть неповний квадрат різниці виразів:

1) x i y; 2) c i d; 3) р i 1; 4) 2 i c.

2. Назвіть неповний квадрат суми виразів:

1) т і п; 2) р і q; 3) а і 1; 4) 3 і х.

Виконання письмових вправ

1. Спростіть вирази:

1) (а – b)(а² + аb + b²);  2) (с + d)(с² – сd + d²);

3) (т – п)(т² + тп + п²);  4) (х + у)(х² – ху + у²).

2. Перетворіть у многочлен стандартного вигляду:

1) (х² – 1)(х⁴ + х² + 1) + 1;  2)(а² + b ²)(а² – а²b² + b⁴) – а⁶ – b⁶;

3) (а + 2)(а² – 2а + 4) – (а – 2)(а² + 2а + 4);

4) (х + 2)(х² – 2х + 4) – х(х – 3)(х + 3);

5) (7а² – 1)(49а⁴ + 7а² + 1) – 4а²(5а² – 1)² + (5а² – 3)(3 – 8а²);

6*) (a + 1)(а – 1)(а² – а + 1)(а² + а + 1)(а⁶ + 1)(а¹² + 1)(а²⁴ + 1).

* Під час виконання цього завдання бажано домогтися від учнів розумін­ня того, що дії кожного учня при перетворенні цілих виразів повинні бути не спонтанними, а свідомими, тобто підкорятись певній послідовності:

1) Встановлюємо порядок виконання дій, визначений умовою задачі.

2) Шукаємо у виразі добутки, які можна перетворити у многочлен за формулами (не забуваємо про можливість застосування законів мно­ження та властивостей степеня).

3) Якщо добутки многочленів не відповідають жодній з формул, вико­ристовуємо алгоритм множення многочленів.

4) Після виконання множення використовуємо інші дії з многочленами (додавання, віднімання, зведення подібних доданків).

3. Розв'яжіть рівняння:

1) (х – 2)(х² + 2х + 4) = х³ + 4х;   2) (у² – 3у + 9)(у + 3) = 6у + у³;

3) (4 – 5х)(16 + 20х) + 25х² + 5х(5х – 2)(5х + 2) = 4;

4) .

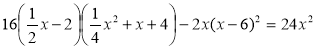4* (додатково). Логічні вправи (на повторення). Яке число або вираз пропущені?

VII. Підсумки уроку

Заповніть пропуски, щоб записи стали правильними:

1) ...суми двох виразів на неповний квадрат їх... дорівнює... кубів цих двох виразів;

2) (... – 1)(a² ... a ... 1) = a³ –  ...

VIII. Домашнє завдання

№ 1. Спростіть вираз:

1) (х – 2)(х² + 2x + 4) – (1 – х)(х² + x + l);

2) (х – 3)(х² + 3х + 9) – (х + 1)(х – 1)(х – 2);

3) а(а – 3)(а + 3) – (а + 2)(а² – 2а + 4);

4) (3а² + 1)(9а⁴ – 3а² + 1) – 3а²(2а² + 1)² + (5а² – 1)(2 – 3а²).

№ 2. Розв'яжіть рівняння:

1) (2 – 3х)(4 + 6х + 9х²) + 3х(3х – 1)(3х + 1) = х;

2) .

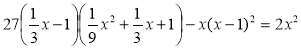№ 3. Випереджальне домашнє завдання.

1) Користуючись відповідним пунктом підручника та записами в зоши­ті, повторіть зміст понять та алгоритмів:

• розкладання на множники;
• винесення спільного множника за дужки;
• розкладання многочленів на множники способом групування.

2) Випишіть у стовпчик усі вивчені формули скороченого множення.

Чи є дані рівності тотожностями? Запишіть ці тотожності, помінявши
місцями ліву та праву частину кожної рівності.