Робочий зошит до теми “Побудова графіка функції за допомогою похідної”

 

 

 

Узагальнення – це мабуть,

найлегший і найочевидніший шлях

розширення математичних знань.

В. Сойер

 

Опорний конспект

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

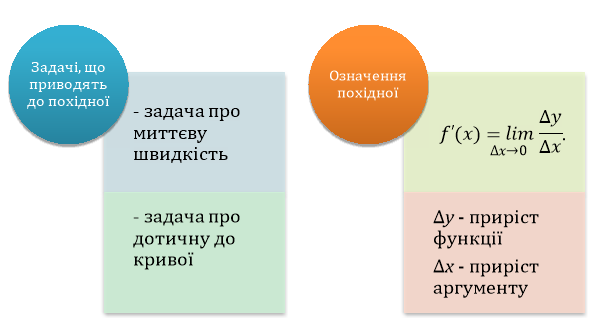
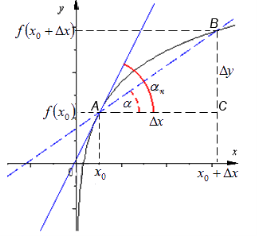
!Функція y=f(x) у точці x₀ називається диференційовною, якщо в цій точці вона має похідну f´(x₀).

!Операція знаходження похідної називається диференціюванням.

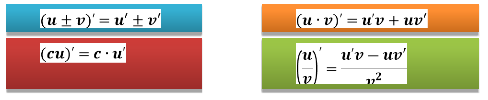
Застосування похідної до дослідження функції

 

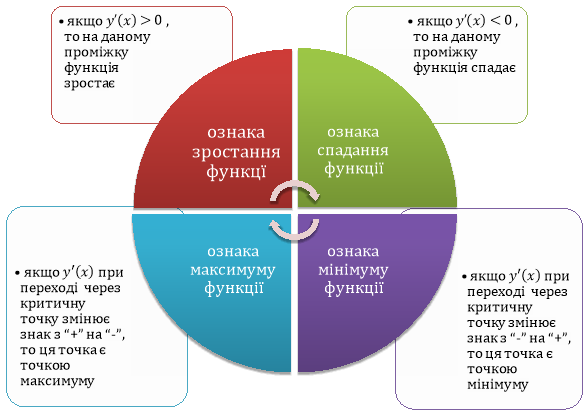
Правило дослідження функції на екстремум

!Точки максимуму та мінімуму називаються екстремумами

Перше правило

1. Знайти критичні точки заданої функції (це точки, в яких похідна дорівнює нулю або не існує).
2. На кожному одержаному проміжку встановити знак похідної.

Друге правило

1. Знайти критичні точки заданої функції.
2. Знайти похідну другого порядку в критичній точці. Якщо 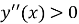, то це точка мінімуму, якщо 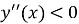, то це точка максимуму.

 

Загальна схема дослідження функції та побудова її графіка

1. Знайти область визначення функції
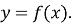
2. Знайти точки перетину з осями координат.
3. Дослідити на парність (непарність), періодичність.
4. Знайти критичні точки.
5. Встановити інтервали монотонності і точки екстремуму.
6. Знайти значення функції в екстремальних точках.
7. Знайти допоміжні точки і на основі дослідження побудувати графік функції.

Результати дослідження заносять до таблиці.

 

 

 

Пам’ятайте:

Якщо ви хочете навчитись плавати,

То сміливо заходьте у воду,

А якщо хочете навчитись розв’язувати задачі,

То розв’язуйте їх.

Д. Пойа

 

 

1. Знайти похідну функції:

а)

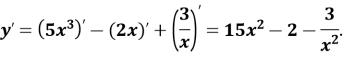
б)

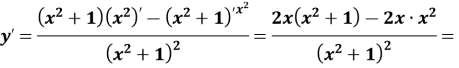
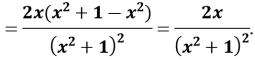
в)

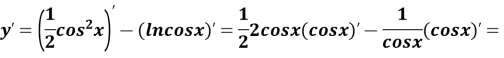
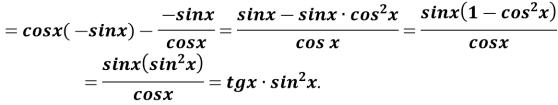
2. Скласти рівняння дотичної до графіка функції 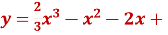3

В точці A(3;6).

Рівняння дотичної має вигляд:

тобто

3. Знайти швидкість і прискорення руху точки при t = , якщо вона рухається за законом

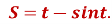
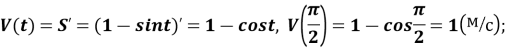
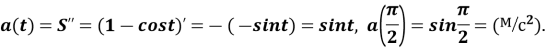
4. Дослідити на екстремум функцію .

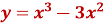Знаходимо похідну функції:

Прирівнюємо її до нуля та з одержаного рівняння знаходимо критичні точки:

Встановлюємо проміжки монотонності:

x	(-	0	(0;2)	2	(2;∞)
f(x)	+	0	-	0	+
f´(x)	↑	0	↓	0	↑
		max		min

 Зміна знака похідної з “+” на “–” означає, що дана функція при x=0 має максимум, а зміна знака похідної з  “–” на “+” показує, що точка x=2  за ознакою є точкою мінімуму.

Знайдемо  максимальне та мінімальне значення функції:

Точка (0;0) – точка максимуму, точка (2;-4) – точка мінімуму.

 

5.               Якими повинні бути розміри закритого циліндричного бака об'ємом 250π см³, щоб на його виготовлення пішла найменша кількість матеріалу.

Побудуємо математичну модель.  Умову задачі переформулюємо так: знайти розміри прямого кругового циліндра із об’ємом 250π см³, що має найменшу площу поверхні. Величинa, яку потрібно оптимізувати, є площа повної поверхні циліндра. Площа повної поверхні циліндра залежить від радіуса основи та висоти циліндра. Отже,  визначити радіус основи R і висоту H циліндра так, щоб при заданому об’ємі площа його поверхні була найменшою S=2πRH+2πR². Найменше значення цієї функції і потрібно обчислити.

 V=πR²H=250π. H=(250π)/(πR²)=250/R², тоді S=(500π)/R+2πR². Отже, математичною моделлю даного завдання є задача знайти найменше значення функції S=(500π)/R+ 2πR².

1. Область визначення функції R₊.
2. Знаходимо похідну: S'=(-500π)/ R²+ 4πR.
3. Знайдемо критичні точки:(-500π)/ R²+ 4πR=0, 4πR³=500π, R³=125, R=5.
4. Знаходимо другу похідну: S"=1000 π/ R³+4π.
5.  S"(5)>0, то при R=5 функція досягає мінімуму, який і є найменшим значенням функції S. Тоді H=250/R², H=10см.

 

6.    Дослідити функцію 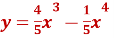 та побудувати її графік.

Колективна робота

 

Не все на світі просто, але є

Якась закономірність саме в тому,

Що істина раптово постає

Крізь ліс ускладнень, в самому простому.

 

Робота в групах

 

Відділ №_______

Дослідити та побудувати графік функції ________________________________

Загальна схема дослідження функції

Область визначення функції:

Знайдемо точки перетину з осями координат.

З віссю Oy:

З віссю Ох:

Дослідимо функцію на парність, непарність.

Знайдемо критичні точки функції, проміжки монотонності, екстремуми.

Знайдемо значення функції в екстремальних точках.

Координати допоміжних точок:

Результати дослідження

x

f´(x)

f(x)

На основі досліджень побудуємо графік функції на міліметровому папері.

Задача 1. Концентрація ліків у крові хворого через t секунд після ін’єкції задається формуло . Знайти максимальну концентрацію і час, коли вона досягається.

Задача 2. Побудувати графік функції .

Задача 3.Тестові завдання:

 

 

 

Розв’язання

Задача 1.

Задача 2.

Задача 3.

Добре засвоєна мудрість не забувається ніколи.

Піфагор

 

1. Що називається функцією?
2. Що таке область визначення функції?
3. Яка функція називаєтьсяя зростаючою (спадною)?
4. Дайте означення похідної функції.
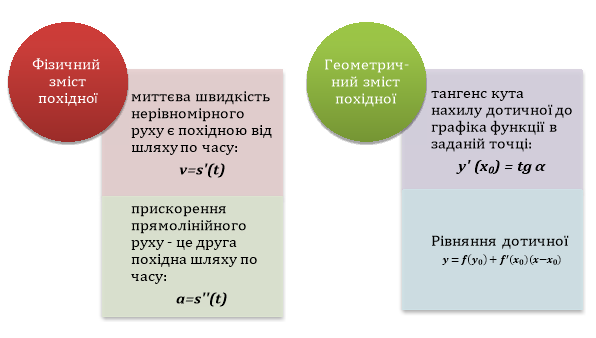
5. В чому полягає геометричний зміст похідної?
6. В чому полягає фізичний зміст похідної?
7. В чому полягає фізичний зміст другої похідної?
8. Складіть рівняння дотичної до кривої y = tg 2x в початку координат.
9. Напишіть правила диференціювання.
10. Сформулюйте умови зростання і спадання функції.
11. Яка точка називається критичною для функції?
12. Як дослідити функцію на  екстремум?
13. За якою схемою проводиться дослідження функції з метою побудови її графіка?

Історична довідка

У 1666 році Ісаак Ньютон і дещо пізніше Готфрід Лейбніц незалежно один від одного побудували теорію диференціального числення. І. Ньютон прийшов до поняття похідної, розвязуючи задачі про миттєву швидкість, а Г. Лейбніц – розглядаючи геометричну задачу про проведення дотичної до кривої.

Ньютон і Лейбніц досліджували проблему максимумів і мінімумів функцій. Зокрема, Лейбніц сформулював теорему про достатню умову зростання і спадання функції на відрізку.

Леонард Ейлер у праці “Диференціальне числення” (1755 р.) розрізняв локальний екстремум і найбільші та найменші значення функції на певному відрізку. Він перший почав використовувати грецьку букву ∆ для позначення приросту аргументу ∆x=x₂ – x₁ та приросту функції ∆y=y₂ – y₁.

Позначення похідної y´, f´(x) ввів французький математик Жозеф Луї Лагранж (1736-1813).