Робота МАН на тему МАТЕМАТИЧНІ НЕСПОДІВАНКИ ТА КУРЙОЗИ
РІВНЕНСЬКА МАЛА АКАДЕМІЯ НАУК УЧНІВСЬКОЇ МОЛОДІ Робота на тему
МАТЕМАТИЧНІ НЕСПОДІВАНКИ ТА КУРЙОЗИ
1
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
УПРАВЛІННЯ ОСВІТИ І НАУКИ РІВНЕНСЬКОЇ ОБЛДЕРЖАДМІНІСТРАЦІЇ
РІВНЕНСЬКА МАЛА АКАДЕМІЯ НАУК УЧНІВСЬКОЇ МОЛОДІ
Відділення математики
Секція математики
МАТЕМАТИЧНІ НЕСПОДІВАНКИ ТА КУРЙОЗИ
Роботу виконав:
Карпінський Рувим Миколайович,
учень 9 класу
Вербівської гімназії»
Дубровицького району
Рівненської області
Науковий керівник:
Бруцька Людмила Василівна,
учитель математики,
спеціаліст І категорії
Тези до науково-дослідницької роботи з теми:
«Математичні несподіванки та курйози»
Автор: Карпінський Рувим Миколайович, учень 9 класу
Науковий керівник: Бруцька Людмила Василівна, учитель математики,спеціаліст ІІ категорії.
Рівненська Мала академія наук учнівської молоді. Вербівська гімназія Рівненської області Дубровицького району с. Вербівка
Актуальність обраної теми обумовлена тим, що сьогодні рівень освіти у світі є досить високим. Для того, щоб розв’язувати складні завдання потрібно розвивати логічне мислення, а логічне мислення розвивається за допомого головоломок. Щодня людина зустрічається з різноманітними числами, вона навіть не здогадується про їх цікаві властивості.
Мета роботи: ознайомитись з історією виникнення головоломок, навчитись розв’язувати логічні завдання, дізнатись про винахідників та дослідників найвідоміших головоломок у світі, ознайомитись з властивостями чисел та навчитись відтворювати фокуси.
Для досягнення даної мети визначено такі завдання:
- Розглянути історію виникнення головоломок;
- Ознайомитись з відомими винахідниками та дослідниками математичних курйозів;
- Розв’язати логічні завдання;
- Розглянути теорію про властивості чисел;
- Знайти в додатковій літературі математичні фокуси та розібратись з їх секретами.
ЗМІСТ
ВСТУП………………………………………………………………… 4
РОЗДІЛ І. РОЗВИТОК ГОЛОВОЛОМОК ТА ЇХ ВПЛИВ НА СУСПІЛЬСТВО………………………………………………………. 6
1.1 Розвиток логіко-математичних завдань………………………… 7
1.2. Вплив головоломок на суспільство…………………………….. 7
РОЗДІЛ II. НАЙВІДОМІШІ МАТЕМАТИЧНІ НЕСПОДІВАНКИ ТА КУРЙОЗИ……………………………………………………………... 9
2.1 Відомі винахідники та дослідники математичних курйозів…… 9
2.2 Відомі логічні іграшки……………………………………………. 9
2.3 Софізми та паралогізми…………………………………………....10
2.4 Логічні задачі та математичні головоломки…………………......11
РОЗДІЛ ІІІ. ВЛАСНІ ДОСЛІДЖЕННЯ………………………..….......13
3.1 Властивості чисел…………………………………………………...13
3.2 Числові курйози………………………………………………….......13
3.3 Демонстрація чисел та їх властивостей серед публіки…………..14
ВИСНОВОК…………………………………………………………………….17
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………...….18
ДОДАТКИ………………………………………………………...……..19
ВСТУП
Люди з давніх часів спостерігали за навколишнім середовищем. Для опису предметів, їх порівняння потрібно використовувати числові значення. Раніше не для всіх була зрозумілою лічба, проте у процесі еволюційного розвитку людина змогла осягнути це вміння. Сьогодні рахувати кожна людина навчається непомітно, під час перших фаз соціалізації. Внаслідок виникнення та розвитку чисел з’явилась наука про їхні властивості та закони, які ними керують – теорія чисел.
Виконуючи різноманітні математичні дії можна помітити не лише загальні властивості всіх чисел, а й особливості окремих числових груп. Ці особливості зазвичай не мають великого важливого теоретичного значення, але вони можуть бути надзвичайно цікавими. Сьогодні ми можемо почути словосполучення, яке для розмовної мови незвично звучить - математичний курйоз, це незвичайний, дивний випадок в математиці.
Актуальність обраної теми обумовлена тим, що сьогодні рівень освіти у світі є досить високим. Для того, щоб розв’язувати складні завдання потрібно розвивати логічне мислення, а логічне мислення розвивається за допомого головоломок. Також сьогодні прилавки іграшкових магазинів поповнюються великою кількістю логічних іграшок. Щодня людина зустрічається з різноманітними числами, вона навіть не здогадується про їх цікаві властивості.
Об’єкти дослідження: математичні несподіванки та курйози.
Предмети досліджень: числа і головоломки.
Мета роботи: ознайомитись з історією виникнення головоломок, навчитись розв’язувати логічні завдання, дізнатись про винахідників та дослідників найвідоміших головоломок у світі, ознайомитись з властивостями чисел та навчитись відтворювати фокуси .
Для досягнення даної мети мною визначено такі завдання:
1) Розглянути історію виникнення головоломок;
2) Ознайомитись з відомими винахідниками та дослідниками математичних курйозів;
3) Розв’язати логічні завдання;
4) Розглянути теорію про властивості чисел;
5) Знайти в додатковій літературі математичні фокуси та розібратись з їх секретами.
Структура роботи: робота містить 3 розділи, 13 малюнків та 6 джерел літератури та 8 інтернет-ресурсів.
РОЗДІЛ І. РОЗВИТОК ГОЛОВОЛОМОК ТА ЇХ ВПЛИВ НА СУСПІЛЬСТВО
Головоломка – це завдання, для виконання якого використовується кмітливість, а не знання високого рівня.
Деякі головоломки відомі з глибокої давнини. Оригінальні логічні задачі знаходять на стінах єгипетських пірамід, в давньогрецьких манускриптах, в інших історичних пам'ятках. Епохою розквіту в середньовічній історії головоломок можна вважати кінець IX століття. Зростання рівня освіти і зниження релігійної нетерпимості до наук привели до розширення кола любителів логічних задач.
Найбільш широке поширення головоломки отримали на рубежі XIX і XX століть. Завдяки діяльності американця Сема Лойда і англійця Генрі Дьюдені головоломки проникли в багато періодичних видань, стали популярними серед широких верств населення. Лойд довгий час вважався автором популярної в усьому світі головоломки «П'ятнашки». Головоломка була настільки популярною, що деякі роботодавці змушені були видати наказ про заборону принесення її на роботу.
Наступним поштовхом у розвитку головоломок став винахід в 1974 році угорцем Ерне Рубіком знаменитого кубика. Кубик Рубіка став не тільки іграшкою, а й об'єктом досліджень математиків і інженерів. З тих пір по всьому світу регулярно проводяться змагання зі швидкісного збирання кубика. Сучасна індустрія головоломок стрімко розвивається. Постійно на ринку з'являються нові ігри, конструкції і видання, покликані тримати інтелект людини в тонусі, розвивати логіку, тренувати нестандартне мислення і підвищувати інтелектуальний рівень в цілому.
1.1 Розвиток логіко-математичних завдань
У давній Месопотамії , майже п’ять тисяч років тому, складали та розв’язували алгебраїчні задачі на знаходження невідомої величини.
Шотландський єгиптолог Хінд знайшов папірус, датований XVII століттям до нашої ери, присвячений математиці. Це був світоч довжиною біля 5,5 метрів та шириною біля 15 сантиметрів. Задача з папірусу під номером 79 мала наступний зміст: « У 7 домах тримають по 7 кішок. Кожна кішка ловить по 7 мишей в день, а кожна миша, якби залишилась живою, то з’їла б в той же день 7 колосків пшениці. Якщо кожний колосок може дати 7 гектарів зерна, то скільки всього тут перераховано?».
Математика формувалася нерівномірно, у різні часи в її розвиток внесли свій вклад Вавилон, Давня Греція, Китай, Індія.
Давньогрецький математик Діофант майже через 2000 років після створення папірусу Хінда запропонував таку задачу: «Знайти три числа, котрі при парному додаванні дають у сумі 20, 30 і 40».
Ірландець Алклуїн склав першу у Європі збірку головоломок та логічних задач, вона мала назву «Задачі для розвитку молодого розуму». Вона з’явилась у другій половині IX століття , написана на латині, складалась з 53 задач.
Розвитку головоломок спонукало підвищення загальної освіченності населення, що збільшило коло людей, які були зацікавлені головоломками. Також у Європу були завезені шахи, які розвивали логічне мислення. З часом люди створювали різноманітні ігри, які пов’язувались з логікою.
1.2. Вплив головоломок на суспільство
Всім відомо, що головоломки розвивають логічне мислення. Логічне мислення відіграє надзвичайно важливу роль у житті людини, адже воно допомагає швидко вирішити незвичайні завдання, що постають перед нею. Маючи хорошу логіку людина може створювати різноманітні винаходи.
У XIX-XX століттях значний вплив на суспільство мала головоломка «гра в 15».
Винайшов цю гру Сем Лойд. Ця гра стала популярною серед робітників фірм, тому роботодавці змушені були заборонити грати в неї у робочий час. « Гра в 15» складається з 15 однакових плоских фішок у вигляді квадратів зі стороною в 1 лінійну одиницю. Усі фішки пронумеровані числами від 1 до 15 і знаходяться у відкритій квадратній коробочці 4 на 4 лінійні одиниці так, щоб лишилося одне вільне місце. Будь-яку з фішок можна пальцем пересунути на порожнє місце. Суть гри полягає у тому, щоб розставити фішки рядами згідно послідовності нанесених на них номерів. Лойд запропонував декілька тисяч доларів тому, хто виконає завдання гри. Але хитрість головоломки полягала у тому, що її неможливо було розв’язати, при багато чисельних спробах виявилось, що всі числа від 1 до 13 виходить скласти, а 14 і 15 помінялись місцями.
Сьогодні індустрія головоломок продовжує бурхливо розвиватися, щорічно поставляючи на ринок нові товари, що дозволяють нам не просто змарнувати час, а в ігровій формі дати навантаження для мозку, навчитись нестандартно мислити і діяти.
РОЗДІЛ II. НАЙВІДОМІШІ МАТЕМАТИЧНІ НЕСПОДІВАНКИ ТА КУРЙОЗИ
2.1 Відомі винахідники та дослідники математичних курйозі
Велику роль у розвитку головоломок відіграли Сем Лойд та Ерне Рубік.
Сем Лойд [мал. 1]– американський шахіст, шаховий композитор, автор головоломок. Авторству Лойда помилково приписується «Гра в 15». Сем швидко навчився грати у шахи і вже з 14 років почав публікувати в газетах шахові задачі. У 16 років він став редактором відділу завдань у щомісячному журналі. У 1871 році Лойд придумав головоломку з картону, яку продав за 10 тисяч доларів, що на той час були величезною сумою. Надалі його головоломки користувалися величезним успіхом. У 1878 році шахіст випустив книгу «Шахова стратегія», до якої увійшли 500 його завдань. Найвідомішими його завданнями були: «Карл ХІІ в Бендерах»[мал. 2], «Екскльсіор»(мат в 5 ходів)[мал. 3], «Погоня любові»(мат в 3 ходи)[мал. 4].
Ерне Рубік [мал. 5] – угорський винахідник, скульпор, професор архітектури. Всесвітньо відомий завдяки своїм об’ємним головоломкам та іграшкам, серед яких Кубік Рубіка(1974 р.)[мал. 6]. Нині в основному бере участь у розробці відеоігор, пише статті з архітектури, очолює студію Рубіка. Нагороджений Державною премією Угорської Народної Республіки(1983 р.), премією імені Денніса Габора(1995 р.), Кошутовською премією(2007 р.).
2.2 Відомі логічні іграшки
Кубик Рубіка [мал. 6]– механічна головоломка, яку винайшов у 1974 році угорський скульптор, винахідник Ерне Рубік. Вже продано понад 300 000 000 екземплярів іграшки у всьому світі. Регулярно у світі проходять змагання на швидкість збирання кубика. Доведено, що кубик можна зібрати не менш як за 23 повороти.
Змійка Рубіка[мал.7] – головоломка, придумана Ерне Рубіком: 24 шарнірно з’єднані між собою призми в перерізі рівнобедреного прямокутного трикутника. Існують версії змійки на 48, 60 та більше ланок. Завдання полягає в складанні різного роду геометричних фігур, тварин, предметів побуту. На початку 1980-х років змійка Рубіка була дуже популярною і досі залишається одним із «бестселерів» серед механічних головоломок, порівняних за популярністю з кубиком Рубіка. З цієї головоломки можна скласти понад 100 двовимірних та тривимірних фігур. Дуже добре розвиває просторове мислення.
Пірамідка Мефферті [мал. 8]– головоломка у формі правильного тетраедра. Кожна грань тетраедра поділена на 9 правильних трикутників. Завдання полягає у тому, щоб перевести пірамідку в конфігурацію з гранями однакового кольору.
2.3 Софізми та паралогізми
Всі ми схильні помилятися: свідомо чи несвідомо . Досить поширеними є логічні помилки. Логічні помилки поділяються на дві групи: софізми та паралогізми
Софізми – свідоме порушення правил і законів раціонального теоретичного мислення. Ціль софізму – видати неправду за істину.
Паралогізми – ненавмисна логічна помилка, пов’язана з порушенням законів і правил логіки.
Паралогізми слід відрізняти від софізмів – помилок, вчинених навмисно, з метою ввести в оману опонента, обґрунтувати помилкове твердження.
Для того, щоб краще розрізняти ці помилки потрібно розглянути приклади.
Софізм.
3=5?
Маємо очевидну рівність
25-15-10=15-9-6
5(5-3-2)=3(5-3-2)
5=3.
Насправді помилка полягає у тому, що виконане ділення на нуль.
Має бути так (5-3)*(5-3-2)=0
2*0=0
0=0
У софізмах є неясне передбачення багатьох конкретних законів логіки, відкритих набагато пізніше. Особливо часто обігрується в них тема неприпустимості протиріч у мисленні.
— Скажи, - звертається софіст до молодого аматора суперечок, - може та сама річ мати якусь властивість і не мати її?
— Очевидно, ні.
— Подивимося. Мед солодкий?
— Так.
— І жовтий теж?
— Так, мед солодкий і жовтий. Але що з цього?
— Виходить, мед солодкий і жовтий одночасно. Але жовтий - це солодкий чи ні?
— Звичайно, ні. Жовтий - це жовтий, а не солодкий.
— Виходить, жовтий - це не солодкий?
— Звичайно.
— Про мед ти сказав, що він солодкий і жовтий, а потім погодився, що жовтий значить не солодкий, і тому як би сказав, що мед є солодким і не солодким одночасно. Але ж спочатку ти твердо говорив, що жодна річ не може володіти і одночасну не мати цю ж властивість.
Звичайно, софісту не вдалося довести, що мед має суперечливі одна одній властивості, будучи солодким і несолодким одночасно. Подібні твердження неможливо довести: вони несумісні з логічним законом протиріччя, що говорить, що висловлення і його заперечення ("мед солодкий" і "мед не є солодким") не можуть бути істинними одночасно.
2.4. Логічні задачі та математичні головоломки
- Іван і Дмитро вийшли назустріч один одному з двох сіл, відстань між якими 20 км. Швидкість Івана 6 км/год, а Дмитра – 4 км/год. Одночасно з Іваном назустріч Дмитру вилетіла муха, Долетівши до Дмитра, вона розвенулась і полетіла до Івана, і так вона літала між ними доти, доки вони не зустрілися. Скільки кілометрів налітала муха, якщо її швидкість 11км/год?
Розв’язання: Звичайно, при розвязуванні цієї задачі можна вдатися до підрахунку відстаней, які щоразу пролітала муха. Однак є більш зручний спосіб розв’язання, адже насправді муха літала стільки часу, скільки витратили наші герої, щоб зустрітися, тобто 20:(6+4)=2 (год). Знаючи, що швидкість мухи становила 11 км/год, легко підрахувати, що відстань, яку вона пролетіла, дорівнює 2*11=22(км).
Відповідь: 22 км.
- Який знак потрібно поставити між цифрами 2 і 3, щоб мати число більше за 2, але менше за 3?
Відповідь: кому.
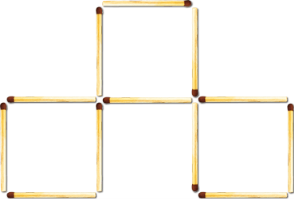
- Завдання з сірниками. Дванадцять сірників лежать так, як показано на мал. 9
Скільки тут квадратів?
Виконайте наступні завдання:
- Заберіть 2 сірника так, щоб утворилось 2 нерівні квадрата. (відповідь мал. 10)
- Перекладіть 2 сірники так, щоб утворились 3 рівних квадрата.(відповідь мал. 11)
- Перекладіть 4 сірники так, щоб утворилось 10 квадратів.(відповідь мал. 12)
РОЗДІЛ ІІІ. ВЛАСНІ ДОСЛІДЖЕННЯ
- Властивості чисел
Майже у всьому світі користуються тепер єдиною системою чисел – десятковою. У цій системі є лише 10 цифр: 1,2,3,4,5,6,7,8,9,0.
Для спостережень над курйозними властивостями чисел візьмемо найбільше та найменше 9-цифрове число, яке складається з 9 різних цифр, застосовуючи звичайну, загальноприйняту форму запису числа.
Найменше – а, а=123 456 789, найбільше – b, b= 987 654 321.
Різниця b-а складається з тих самих цифр:
987 654 321-123 456 789=864 197 532
Помічаємо, що цифри не повторюються.
Якщо а помножити на 8 і додати 9, то отримуємо b:
123 456 789*8+9=987 654 321
- Числові курйози
Дуже легко запам’ятати квадрати таких чисел, як 11, 111, 1111, … А саме:
112=121
1112=12321
11112=1234321
…
Квадрати цих чисел також володіють цікавими та незвичайними властивостями.
1+2+1=4= 22
1+2+3+2+1=9=32
1+2+3+4+3+2+1=16=42
…
Крім того, кожне з цих чисел можна представити у вигляді цікавих по формі запису неправильних дробів:
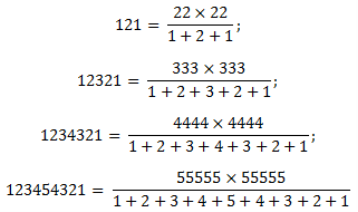
3.3 Демонстрація чисел та їх властивостей серед публіки
Співпадаюче число
Передайте глядачеві папірець і скажіть, що на ньому ви написали число , воно не менше 1 і не більше 50 . І нехай він, не дивлячись на цей папірець , покладе його в кишеню. Коли глядач сховає папірець , нехай візьме інший клаптик і напише на ньому яке-небудь число від 50 до 99 так , щоб ви не бачили.
Тепер скажіть йому одне число, яке він повинен додати до свого числа, закреслити першу цифру результату зліва і додати її до того, що у нього вийде. Після цього запропонуйте відняти свій результат від того числа, яке він задумав, і подивіться , що написано на вашому папірці . На ньому буде стояти те ж саме число.
Секрет фокусу: На папірці , який глядач, не дивлячись, сховав у кишеню, ви написали, наприклад, число 23 (не менше 1 і не більше 50). Коли глядач задумає число ( від 50 до 99 ) , яке ви не знаєте , назвіть йому число 76 і нехай додасть його до свого числа. Число 76 ви взяли не навмання - в цьому вся хитрість.
Ви відняли написане вами число 23 від 99 і отримали 76 . Якби ви написали на папірці не 23, а, скажімо, 40, ви веліли б глядачеві скласти з його числом не 76, а 99 - 40, тобто 59. І потім у відповіді у нього вийшло б 40, скільки б він не задумав.
Припустимо, глядач задумав 92. Скажіть йому додати до його числа 59. Коли глядач складе числа , він отримає 151 . Закреслить першу цифру ліворуч - отримає 51. Додасть закреслену цифру - отримає 52. Відніме цей результат від свого задуманого числа: 92 - 52 = 40.
Фокус з календарем
Скажіть присутнім, що легко зможете вирахувати суму 9 будь-яких чисел, які друзі загадають, не знаючи, що це за числа.
Для цього нехай хтось один відмітить на календарі дев’ять чисел так, щоб вони утворили квадрат, а вам назве лише найменше число з відмічених. Ви з легкістю швидко назвете суму закреслених чисел.
Секрет цього фокусу: до цього названого числа додайте 8, а результат помножте на 9. Наприклад, закреслено так, як показано на мал. 13. Отож, найменшою є цифра 3. Далі робимо таким чином: 3+8=11, 11*9=99. Оголошуємо результат – 99. Ну, тепер нехай присутні додають і перевіряють результат.
Цікавий результат
Для того , щоб виконати даний дослід потрібно загадати 7 цифр(це може бути номер мобільного телефону, без коду оператора чи міста), також потрібно мати при собі калькулятор. Для прикладу візьмемо 1324756
- Для початку потрібно взяти перші три цифри
- Помножити їх на 80
- До отриманого числа додати 1
- Результат помножити на 250
- Тепер потрібно взяти останні 4 цифри, додати їх до попереднього результату
- Повторити дію, тобто знову додати 4 останні цифри
- Тепер потрібно відняти 250
- Отримане число поділити на 2
- Результат вийшов незвичайний
Виконаємо дії для числа 1324756
- 132
- 132*80=10 560
- 10 560+1= 10 561
- 10 561*250=2 640 250
- 2 640 250+ 4756=2 645 006
- 2 645 006+ 4756 = 2 649 762
- 2 649 762– 250 = 2 649 512
- 2 649 512:2 = 1324756
ВИСНОВОК
Світ чисел глибоко проникає у наше життя. Вони є скрізь: на предметах побуту, у техніці, у даті народження, у будь-яких журналах, книгах. Без них мало хто уявляє своє життя. Але ми часто не помічаємо всіх тих властивостей, що можуть нам показати та навчити нас чогось нового числа.
Досліджуючи числа, науковці знаходять небачені раніше їхні властивості. Для людства відкриваються нові курйози та парадокси. Деякі курйози, виявлені століття тому, й досі не під силу розв’язати найкращим розумам планети, але вирішуючи ці проблеми, людина рухається вперед до прогресу.
Уже зараз, завдяки дивовижним властивостям чисел, ми можемо демонструвати всю хитрість та швидкість свого розуму.
Також головоломки відіграють важливу роль в житті людини, адже вони позитивно впливають на розвиток логічного мислення людей. Сьогодні неабияк важливою є галузь промисловості, яка виготовляє логічні іграшки. У будь-якому іграшковому магазині можна знайти відомий на весь світ кубик Рубіка, змійку та безліч інших розвиваючих ігор. Також на уроках математики дитина розвиває свою логіку методом розв’язування логічних задач. Навіть за допомогою звичайних сірників можна розвиватись. Також математичні несподіванки та курйози можуть допомогти здивувати друзів. Нині існує безліч різноманітних фокусів, задач-загадок, судоку та інших цікавих завдань, за допомогою яких , при використанні дивовижних властивостей чисел, можна цікаво та весело провести час.
У процесі виконання роботи її мета була досягнута, а завдання вирішені.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Кемені Дж. Д., Снел Дж., Томсон Дж. Л. «Введення в кінцеву математику». – М.: ІЛ, 1963.
2. С. Лойд (мол.), С. Лойд (ст.) «Енциклопедія головоломок». – М.: Мир, 1970.
3. Лойд С. (ст.) «Математична мозаїка» - М.:Мир, 1980.
4. Брукс А. «Логіка фіксованих та зростаючих автоматів» - Технічний Дослідницький Інститут Університету Мічигану, 1961
5. Б. Хеєс «Зльоти та падіння чисел-градин», Scitntific American: №3 березень 1984.
6. Лєбедєв Ю.А. « Про деякі евретичні аспекти послідовності («3n+1» - проблеми в теорії чисел)» - М.:Мир, 1998
ІНТЕРНЕТ-РЕСУРСИ
- http://library.ippro.com.ua/attachments/article/107/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D0%B0%20%D0%BB%D0%BE%D0%B3%D1%96%D0%BA%D0%B0d.pdf
- http://matematiku.ru/index.php?option=com_content&task=view&id=2187&Itemid=32
- http://mathworld.ru/chislovye-kurezy/
- https://ru.wikipedia.org/wiki/%D0%93%D0%BE%D0%BB%D0%BE%D0%B2%D0%BE%D0%BB%D0%BE%D0%BC%D0%BA%D0%B0
- http://allref.com.ua/uk/skachaty/Sofizmi_i_paralogizmi
- http://ru.osvita.ua/vnz/reports/logika/25253/
- http://zagadki.org.ua/ua/riddles/matches/p1/1/
- http://formula.co.ua/uk/category/puzzles/math-puzzles
ДОДАТКИ
Мал. 1 
Мал. 2 
Мал. 3  Мал. 4
Мал. 4 
Мал. 5 
Мал. 6 ![]()

Мал. 7 
Мал. 8 
 мал. 9
мал. 9  мал. 10
мал. 10
 мал. 11
мал. 11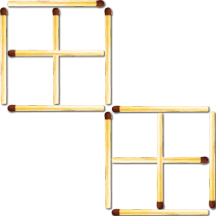 мал. 12
мал. 12
 мал. 13
мал. 13


про публікацію авторської розробки
Додати розробку
