Посібник "Математичний гурток" для 6 класу

Смілянська загальноосвітня школа І-ІІІ ступенів №11

Смілянської міської ради Черкаської області

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний гурток

 

 

 

 

 

 

 

 

                         Математика

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

м. Сміла

2021

Автор: Довга Т.Г., учитель математики Смілянської загальноосвітньої школи І-ІІІ ступенів №11 Смілянської міської ради Черкаської області

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Анотація

      

      Посібник містить методичні рекомендації щодо роботи з обдарованими дітьми, календарне планування математичного гуртка у 6-8 класах та розробки занять математичного гуртка для 6 класу.

      Цікавий матеріал допоможе розвинути творчі здібності  школярів, сприятиме підвищенню інтересу учнів до математики. Оригінальні авторські розробки занять будуть корисними вчителям-практикам у роботі з обдарованими дітьми.

     Для вчителів математики, керівників гуртків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

Передмова             4

Тематичне планування  5-8 класи                                                                                    6

6 клас

Заняття 1-2 Повторення матеріалу за 5-й клас. Розв’язування логічних задач   8

Заняття 3-4 Подільність та остача. Алгоритм Евкліда.     10

Заняття 5-9 Принцип Діріхле.         12

Заняття 10-14 Задача Пуассона. Задачі на переливання.     16

Заняття 15-18 «Рятівні круги» великого Ейлера.      19

Заняття 19-23 Задачі, які розв’язуються з кінця.      21

Задача 24-28 Розв’язування старовинних цікавих задач.     23

Задача 29-33 Розв’язування логічних задач.       26

Задача 34-35 Розв’язування олімпіадних задач.       29

Задача 36-37 Математичні ребуси, шифровки, таємничі історії.    32

Література             35
Передмова

Одним з видів позакласної роботи з математики в школі є математичні гуртки. Викликаючи інтерес учнів до предмету, гуртки сприяють розвитку математичного кругозору, творчих здібностей учнів, прищепленню навичок самостійної роботи і тим самим підвищенню якості математичної підготовки учнів.

 Іх доповнюють одноразові заходи, що проводяться в школі (математичні вечори, вікторини, олімпіади, КВК, змагання команд та інше), так і поза школою (математичні конкурси, що проводяться окремими газетами, журналами, вищими навчальними закладами, «Золотий ключик», міжнародний математичний конкурс «Кенгуру» та інші).

 В зв’язку з переходом шкіл на нову 12-річну програму з математики, пропоную відповідне планування гурткової роботи виходячи з власного досвіду роботи. До плану роботи гуртка вважаю за доцільне включати питання, яких не має у програмі, розв’язування цікавих задач. Розподіл годин є орієнтовним. Учитель може вносити зміни щодо розподілу годин, відведених на вивчення теми, змінювати послідовність їх розгляду, конкретизувати зміст кожного заняття.

 Заняття гуртка у 5-6-х класах можна проводити за таким планом:

І. Організаційна частина.

ІІ. Мотивація навчальної діяльності, сприймання і осмислення навчального матеріалу.

ІІІ. 1. Пояснення вчителем теми заняття методом евристичної бесіди.

      2. Виконання завдань учнями по темі.

      3. Гра, математичні фокуси.

      4. Математична бійка, математичний бій, математичний хокей, математичний аукціон або інше.

 В даній роботі пропоную тематичне планування для 5-8 класів та розробки  занять гуртка для 6 класу.

 Заняття математичного гуртка в старших класах проводжу за таким планом:

1. Доповідь одного з учасників гуртка на 5-10 хв. з історії математики; повідомлення керівника або учасника гуртка по темі заняття;
2. Розв’язування задач, в тому числі підвищеної складності;
3. Розв’язування задач цікавого змісту та задач на кмітливість;
4. Ознайомлення учасників гуртка з задачами, що були запропоновані при незалежному зовнішньому тестуванні, на вступних екзаменах до технікумів, ВНЗ.
5. Відповіді на різні запитання учнів.

Знайомство з конкурсними задачами допоможе учням мати повне уявлення про вимоги з математики при вступі до вищих навчальних закладів. З умовами таких задач доцільно знайомити учасників у кінці кожного заняття, а їх розв’язування можна пропонувати бажаючим для самостійної роботи вдома. Слід мати на увазі, що виконання домашніх завдань не є обов’язковим.

5 клас

Тематичний план

№ п/п	Тема	Кількість годин
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.	Організаційне заняття. Техніка усного рахунку. Як грати , щоб не програти. Вчимося розв’язувати задачі. Задачі, які розв’язуються з кінця. Задачі на переливання. Математика на сірниках. Розв’язування логічних задач. Розв’язування олімпіадних задач. Розв’язування старовинних цікавих задач. Математичні ребуси, шифровки, таємничі історії.	2 2 3 2 2 3 6 4 6 5
	Всього	35

 

 

6 клас

Тематичний план

№ п/п	Тема	Кількість годин
1.   2. 3.   4. 5. 6. 7. 8. 9. 10.	Організаційне заняття. Повторення матеріалу за 5-й клас. Розв’язування логічних задач. Подільність та остача. Алгоритми Евкліда. Принцип Діріхле: «Клітки і зайці», «Знайомства», «Подільність», «Геометрія», «Рано чи пізно повториться», «Додаткові задачі». Задача Пуассона. Задачі на переливання. «Рятівні круги» великого Ейлера. Задачі, які розв’язуютсья з кінця. Розв’язування старовинних цікавих задач. Розв’язування логічних задач. Розв’язування олімпіадних задач. Математичні ребуси, шифровки, таємничі історії.	2 2   4 4 2 4 5 5 5 2
	Всього	35

 

 

 

 

 

 

7 клас

Тематичний план

№ п/п	Тема	Кількість годин
1.   2. 3. 4.     5. 6. 7. 8. 9. 10. 11.	Повторення матеріалу за 6-й клас. Розв’язування задач логічного характеру Розв’язування задач на відсотки. Розв’язування задач на «суміші». Розв’язування задач на «рух». Графіки руху. Зустрічі в океані. Стрілки обходять циферблат. Джентльмени на прогулянці. Задачі Ісаака Ньютона. Задачі на пошук предмета. (фальшива монета…) Задачі на «роботу». Розв’язування логічних задач. Розв’язування олімпіадних задач. Розв’язування задач на побудову. Різні системи числення. Графіки функцій.	2 4 4     5 2 4 4 4 2 2 2
	Всьоого	35

 

8 клас

Тематичний план

№ п/п	Тема	Кількість годин
1.   2. 3. 4. 5.   6. 7. 8. 9. 10. 11.	Організаційне заняття. Повторення матеріалу за 7-й клас. Розв’язування задач логічного характеру Функції та їх графіки. Розв’язування систем лінійних рівнянь через детермінант. Розв’язування алгебраїчних, геометричних задач Знайомство з життям та діяльністю відомих математиків Ф. Вієта та Р. Декарта. Формула відстані між двома точками. Модуль числа. Графіки та рівняння, що містять знак модуля. Життя та діяльність жінок-математиків у різні часи. Розв’язування геометричних та алгебраїчних задач Розв’язування олімпіадних задач. Розв’язування задач із збірника міжнародного математичного конкурсу «Кенгуру».	2 4 4 5   2 4 4 4 2 2   2
	Всього	35

 

Розробки занять гуртка для 6 класу

Заняття 1-2

Тема. Повторення матеріалу за 5 клас. Розв'язування логічних задач

Не можна будувати заняття гуртка, використовуючи тільки задачі "на тему". Необхідні також не­ стандартні задачі, для розв'язання яких треба придумати щось нове, винайти свіжу ідею чи просто подолати які-небудь технічні труднощі. Не обійтися без подібних задач і при складанні олімпіад, матбоїв і т.д.

1. Логічні задачі

Головна мета занять зі школярами молодших класів - навчити їх послідовно мислити: не плутати причину з наслідком, ретельно про­водити перебір, правильно будувати ланцюжки міркувань. Для цього дуже корисні логічні задачі.

Задача 1. Сьогодні Петрикова мама сказала: "Всі чемпіони добре навчаються." Петрик каже: "Я добре вчуся. Значить, я чемпіон." Чи правильно він міркує?

Задача 2. На столі лежать 4 картки, на яких зверху написано: А, Б, 4, 5. Яку найменшу кількість карток і які саме слід перевернути, щоб перевірити, чи вірне твердження: "Якщо на одній стороні картки написано парне число, то на іншій стороні картки — голосна літера"?

Задача 3. В гаманці лежать дві монети на загальну суму 15 копійок. Одна з них — не п'ятак. Що це за монети?

Задача 4. Припустимо, що вірні наступні твердження:

а) серед людей, які мають телевізори, є такі, які не є малярами;

б) люди, які кожний день купаються в басейні, але не є малярами, не мають телевізорів.

Чи випливає звідси, що не всі власники телевізорів кожний день купа­ються в басейні?

Задача 5. В Країні Чудес проводилося слідство по справі про укра­дене борошно. На суді Мартовський Заєць заявив, що вкрав Болванщик. В свою чергу Болванщик і Соня дали свідчення, що з якихось причин не були записані. В ході судового засідання з'ясувалося, що борошно вкрав лише один із трьох підсудних і що тільки він дав правдиві свідчення. Хто вкрав борошно?

Задача 6. В коробці з олівцями є олівці різної довжини і є олівці різного кольору. Доведіть, що є два олівці, що відрізняються і за кольо­ром і за довжиною.

Задача 7. В трьох урнах лежать кулі: в одній — дві білих, в дру­гій — дві чорних, в третій -- біла і чорна. На урнах висять таблички: ББ, ЧЧ і БЧ так, що вміст кожної з урн не відповідає табличці. Як, витягнувши одну кулю, визначити, в якій урні що лежить?

Задача 8. Трьох чоловік — А, В і С — посадили в ряд так, що А бачить В і С, В бачить тільки С, а С нікого не бачить. Потім їм показали 5 ковпаків — 3 червоних і 2 білих, зав'язали очі і натягнули кожному на голову червоний ковпак. Після цього їм розв'язали очі і кожного запитали, чи може він визначити колір свого ковпака. Після того, як А, а потім і В, відповіли негативно, С зрозумів, якого кольору на ньому ковпак. Як він міркував?

*     *     *

В наступних восьми задачах події розгортаються на острові, корін­ними жителями якого є лицарі, що завжди кажуть правду, і брехуни, що завжди брешуть.

Задача 10. Людина А каже: "Я брехун". Чи є він уродженцем остро­ва лицарів і брехунів?

Задача 11. Яке питання треба задати на острові аборигену, щоб дізнатися, куди веде дорога, що цікавить нас, — в місто брехунів чи в місто лицарів?

Задача 12. Яке питання треба задати аборигену, щоб дізнатися, чи живе у нього дома свійський крокодил?

Задача 13. Уявіть собі, що на мові острова слова "так" і "ні" звучать як "тип" і "топ", але невідомо, яке саме слово що означає. Як, задавши аборигену одне питання, з'ясувати у нього, брехун він чи лицар?

Задача 14. Яке питання треба задати аборигену, щоб він обов'язково відповів "тип"?

Задача 15. Островитянин А в присутності іншого островитянина В каже: "Принаймні один із нас — брехун". Хто такий А і хто такий В?

Задача 16. Є три чоловіки: А, В і С, про яких відомо, що один із них лицар, другий — брехун, а третій — приїжджий, нормальний чоловік, який може казати і правду, і брехати.

А каже: "Я нормальна людина".

В каже: "А і С інколи кажуть правду".

С каже: "В — нормальна людина".

Хто з них брехун, хто — лицар, а хто — нормальна людина?

 Задача 17. Зустрілися декілька аборигенів, і кожний з них заявив всім іншим: «Ви всі - брехуни». Скільки лицарів могло бути серед цих аборигенів?

 

Заняття 3-4

Тема. Досконалі числа. Алгоритм Евкліда.

Подільність та остача

1. Прості та складені

Ви, звичайно, добре знаєте, що поміж натуральних чисел є прості та складені. Число виявляється складеним, якщо воно дорівнює до­бутку двох менших натуральних (наприклад,  6 = 2·3). Інше число (якщо воно, крім того, відмінне від 1) називається простим. Одиниця не вважається ні простим, ні складеним числом.

Прості числа виявляються тими "цеглинками", з яких можна побудувати всі інші числа. В якому сенсі? Розглянемо число 420. Воно, без сумніву, складене. Його можна розкласти на множники, наприклад, так: 420 = 42 · 10. Кожне з чи­сел 42 та 10 також складене: 42 = 6·7, 10 = 2·5. Оскільки 6 = 2·3, то 420 = 42·10 = 6·7·2·5 = 2·3·7·2·5 = 2·2·3·5·7. Ми отримали розклад нашого числа на прості множ­ники.

              Напевно, ні в кого не викличе сумніву, що, діючи та­ким чином, можна представити у вигляді добутку про­стих чисел будь-яке натуральне число (крім 1) — треба розкладати співмножники, які отримуються, в добутки менших, поки це      вдається. А що, як спробувати розкласти число 420 на множники по-іншому?

Наприклад, почавши так: 420 = 15 · 28. Ви, певна річ, здо­гадалися, що в результаті дістанеться той же розклад (якщо в кінці прості співмножники розташувати в порядку зростання).

 

Алгоритм Евкліда

 Ми обговорили поняття найбільшого спільного дільника двох натуральних чисел і з’ясували, як можна його знайти: достатньо виписати розклад цих чисел  на прості множники і взяти їх спільну частину. Але для великих чисел ця процедура практично не може бути виконана. Спробуйте, наприклад, таким чином знайти найбільший спільний дільник чисел 1381955 і 690713. На щастя, існує інший метод, який дозволяє обчислити НСД двох чисел. Він називається алгоритмом Евкліда.

 Алгоритм Евкліда ґрунтується на такому міркуванні: будь-який спільний дільник чисел а і b (a >b) ділить також число а – b; крім того, будь-який спільний дільник чисел b і а – b ділить число а. Отже, НСД (а;b)=НСД(b,a-b). Ми, по суті, виклали алгоритм Евкліда.

 Покажемо, як він працює для конкретних чисел. Знайдемо найбільший спільний дільник чисел 451 та 287:

НСД(451,287)=НСД(278,164)=НСД(164,123)=НСД(123,41)=НСД(82,41)=НСД(41,41)=41

 Зауважимо, що алгоритм Евкліда можна прискорити: замінити а не а-b, а зразу на остачу від ділення а на b. Продемонструємо це на прикладі чисел, які наведено на початку:

НСД(1381955,690713)=НСД(690713,529)=НСД(529,368)

           =НСД(368,161)=НСД(161,46)

           =НСД(46,23)=НСД(23,0)=23.

Як бачимо, цей метод дуже швидко приводить до результату.

Задача 1. Знайти найбільший спільний дільник чисел 2n+13 та n +7.

Розв’язок. НСД(2n+13, n+7)=НСД(n+7, n+6)=НСД(n+6,1)=1

                       12n+1

Задача 2*. Доведіть що дріб 30n+2   нескоротний ні при якому натуральному n.

Розв’язання

НСД(30n+2; 12n+1)=НСД(12n+1;6n)=НСД(6n;1)=1

Задача 3*. Знайдіть НСД (2¹⁰⁰ - 1,2¹²⁰-1).

Задача 4*. Знайдіть НСД(111…111, 11…11) -  в запису першого числа 100 одиниць, в запису другого 60.

Алгоритм Евкліда, незважаючи на свою простоту, виявляється важливим елементом математичної освіти.

Заняття 5-8

Тема: Принцип Діріхле

Цілком можливо, що ви вже чули про принцип Діріхле. Тоді він найімовірніше, з'являвся перед вами в такому жартівливому формулюванні "Коли в N клітках сидять не менш N + 1 пташок, то в якійсь із кліток сидить не менш двох пташок". Зверніть увагу на розпливчатість висновків - "в якійсь із кліток", "не менш". Це є, мабуть характерною рисою принципу Діріхле, яка іноді приводить до можливості несподіваних висновків на основі, здавалось би, абсолютно недостатніх відомостей.

Доведення самого принципу надзвичайно просте, в ньому використовується тривіальний підрахунок пташок в клітках. Коли б у кожній клітці сиділо не більше одної пташки, то всього в наших N клітках сиділо б не більше N пташок, що суперечило б умовам. Таким чином, ми довели принцип Діріхле, застосувавши (обов'язково зверніть на це увагу) метод доведення від супротивного.

 

 

 

 Але, запитаєте ви, хіба про пташок йдеться в задачі:

Задача 1. В мішку лежать кульки двох різних кольорів: чорного та білого. Яке найменше число кульок треба вийняти з мішка наосліп так, щоб серед них неодмінно виявилися дві кульки одного кольору?

Наступна задача також не має ніякого відношення до пташок і клі­ток, принаймні судячи з формулювання:

Задача 2. В лісі росте мільйон ялинок. Відомо, що на кожній з них не більше 600000 голок. Доведіть, що в лісі знайдуться дві ялинки а однаковою кількістью голок.

Розглянемо тепер їх розв'язки:

Розв’язок задачі1. Дістанемо з мішка 3 кульки. Якщо б серед цих кульок було не більше однієї кульки кожного з двох кольорів, то всього було б  не більше двох кульок — це очевидно і не суперечить тому, що ми дістали три кульки. З іншого боку зрозуміло, що двох кульок може не  вистачити. Ясно, що пташками тут виявляються кульки, а вітками  кольори: чорний та білий.     

Розв’язок задачі 2. Перед нами мільйон "пташок" - ялинок і, на жаль, всього лише 600001 клітка з номерами від 0 до 600000. Кожна «пташка» - ялинка саджається нами в клітку з номером, який дорівнює кількості голок на цій ялинці. Оскільки "пташок" значно більше, ніж кліток, то в якійсь клітці сидить принаймні дві "пташки" — коли б в кожній сиділо не більше однієї, то всього "пташок"-ялинок було б не більше 600001 штук. Проте, коли дві "пташки"-ялинки сидять в одній клітці, ті кількість голок у них однакова.  

Зверніть увагу на те, що формулювання цих задач носять той же наліт розпливчатості висновку, що й сам принцип Діріхле. Часто саме такі питання і розв'язуються за його допомогою. Ось ще три аналогічні задачі.

Задача 3. Дано 12 цілих чисел. Доведіть, що з них можна вибрати два, різниця яких ділиться на 11.

Задача 4. У місті Санкт-Петербурзі живе 5 мільйонів чоловік. Доведіть, що в якихось двох з них однакове число волосин на голові, якщо відомо, що у будь-якого чоловіка на голові менше мільйона волосин.

Задача 5. До магазину привезли 25 ящиків з трьома різними сортами яблук (в кожному ящику яблука тільки одного сорту). Доведіть, що серед них є принаймні 9 ящиків з яблуками одного й того ж сорту.

Для викладачів. Поговоримо про те, як приблизно проходить занят­тя по нашій темі (не слід думати, що всі заняття гуртка, а це 2-3 години повинні бути присвячені одній темі — це втомлює дітей. Мабуть, краще всього розв'язувати на занятті задачі на дві-три різні теми, не забуваючи і про розважальні задачі). Спочатку діти розв'язують декілька простих вправ, як задача 1 або 2, — іноді вони навіть не розуміють, що ж треба доводити: на прикладі цих та наступних задач необхідно пояснити відміну інтуїтивних міркувань від справжнього доведення. При розгляді цих задач підкресліть спільність ідеї — це для дітей звичайно зовсім не очевидно. Після цього йде серія за­дач на свідоме повторювання міркувань, які тільки що провів викладач (задачі 3-7). Звичайно_, спочатку слід давати простіші задачі. Тільки після цього, як нам здається, можна розповісти дітям про те, що таке принцип Діріхле та підкреслити, що він лежить в основі всіх наведених розв'язків. Намагайтеся в подальшому при розгляді задач іноді подавати розв'язок повністю, навіть без згадування слів "принцип Діріхле" — щоб нагадати дітям про те, що він собою являє. 

Якщо Ви уважно прочитали все, що було написано, і спробували розв'язати задачу 5 так само, як і перші дві, то, скоріше всього, Вам це не вдалося. Тож із принципа Діріхле випливає лише, що є два ящики з яблуками одного сорту. В розв'язанні цієї задачі нам допоможе уза­гальнений принцип Діріхле: "Якщо в N клітках сидять не менше kN+1 пташка, то в якійсь а кліток сидить принаймні k + 1 пташок."

Зверніть увагу на те, що у випадку к = 1 узагальнений прин­цип Діріхле перетворюється в звичайний принцип Діріхле. Доведення цього "узагальненого принципу" залишаємо Вам як вправу.

Розв'язок задачі 5. 25 ящиків-"пташок" розсадимо по 3 "клітках"-сортах. Оскільки

25 = 3·8 + 1, то застосуємо "узагальнений принцил Діріхле" для N = 3, к = 8 і отримаємо, що в якійсь "клітці"-сорті не менше 9 ящиків.

          Якщо Ви розібрали тільки що наведений тут розв'язок, то було б дуже повчальним перевірити, чи змогли б Ви викласти цей ж розв'язок без згадки про будь-який принцип Діріхле, користуючись лише мірку­ваннями типу тривіального підрахунку, за допомого яких ми довели принцип Діріхле.

   В більшості всіх подальших задач на принцип Діріхле необхідно застосовувати саме узагальнений принцип Діріхле. Маємо ще дві за­дачі:

   Задача 6. В країні Курляндії т футбольних команд (по 11 футболіс­тів у кожній). Всі футболісти зібралися в аеропорту для поїздки в іншу країну на відповідальний матч. Літак зробив 10 рейсів, перевозячи за кожним разом по т пасажирів. Ще один футболіст прилетів на місце майбутнього матчу на вертольоті. Доведіть, що хоча б одна команда була в повному складі доставлена в іншу країну.

   Задача 7. Дано 8 різних натуральних чисел, не більших 15. Доведіть, що серед їхніх додатних попарних різниць є три однакових.

       При розв'язанні задачі 7 зустрічається, здавалось би, нездоланна перешкода. Неоднакових різниць може бути 14 — від 1 до 14 — це ті 14 кліток, в які ми будемо саджати кроликів. Хто ж буде нашими пташками? Ними, безумовно, повинні бути різниці між парами за­пропонованих нам натуральних чисел. Проте маємо 28 пар і їх можна розсадити по 14 клітках так, що в кожній клітці буде сидіти рівно дві “пташки" (і значить, в кожній менше трьох). Тут треба скористатися  додатковим міркуванням: в клітці з номером 14 може сидіти не більше одної пташки, адже ж число 14 можна записати як різницю двох натуральних чисел, які не перевищують 15, лише одним спосо­бом: 14 = 15-1. Значить, в 13 клітках, які залишилися, сидять не менше 27 пташок, і застосування узагальненого принципу Діріхле дає дам бажаний результат.

*   *   *

       В серії із чотирьох наступних задач також необхідно застосувати принцип Діріхлє (або узагальнений принцип Діріхле) плюс яке-небудь додаткове міркування.

Задача 8. Доведіть, що в будь-якій компанії з 5 чоловік є двоє, які мають однакове число знайомих в цій компанії.

Задача 9. Декілька футбольних команд проводять турнір в одне коло. Доведіть, що в будь-який момент турніру знайдуться дві команди, які зіграли на цей час однакове число матчів.

Задача 10.

Підказ до подачі 10а. Розбийте дошку на 16 квадратиків 2x2 — це клітинки; пташками, звичайно, будуть чорні поля.

Задача 11. 10 школярів на олімпіаді розв'язали 35 задач, причому відомо, що серед них є школярі, які розв'язали рівно одну задачу, школярі які розв'язали рівно дві задачі, та школярі, які розв'язали рівно три задачі. Доведіть, що є школярі, які розв'язали не менш п'яти задач.

Методичні зауваження. При розгляді задач дуже корисно чітко поділити доведення на пошуки пташок і кліток, додаткові міркування та, нарешті  застосування принципу Діріхле. Конкретною, хоч і не головною, метою для Вас може служити вироблення певного автоматизму в застосуванні принципу Діріхле та навичок у визначенні за зовнішнім виглядом задачі того, що вона — на принцип Діріхле.

 

Заняття 9-12

Тема. Задачі на переливання. Задача Пуассона.

 Задачі на переливання можна розв’язувати:

а) з кінця;

б) методом проб;

в) у вигляді таблиці.

Задача Пуасона.

 Дехто має 12 пінт вина (пінта – старовинна міра рідини, приблизно дорівнює 0,568 л) і має намір подарувати з нього половину, але не має посудини в 6 пінт, а має дві посудини: одна у 8, а друга у 5 пінт. Яким чином можна отримати 6 пінт вина?

 Цю задачу недаремно пов’язують з ім’ям знаменитого французького математика, механіка і фізика Симеона Дені Пуассона (1781-1840). Коли Пуассон був ще дуже молодим і сумнівався у виборі життєвого шляху, приятель показав йому тексти кількох задач, з якими не міг впоратися сам. Пуассон вирішив їх усі менше, як за годину. Особливо йому сподобалась задача про дві посудини.

 - Ця задача визначала мою долю, - говорив він згодом. – Я вирішив, що обов’язково буду математиком.

Розв’язання задачі Пуассона

12	5	8
12	-	-
4	-	8
4	5	3
9	-	3
9	3	-
1	3	8
1	5	6

Що і треба було зробити 

Розв’яжемо ще декілька задач на переливання, починаючи з простих.

Задача (усно). Маємо дві посудини – трилітрову  та п’ятилітрову. Користуючись ними, отримати 1 літр води.

Розв’язання

Ця задача може бути розв’язана усно, заповнимо трилітрову посудину, переллємо з неї воду у п’ятилітрову. Знову заповнимо трилітрову посудину і знову переллємо до країв у п’ятилітрову посудину. При цьому у трилітровій посудині залишиться 1 літр води.

Задача 1. Із посудини на 14 літрів треба відлити 3 літри рідини, користуючись двома порожніми посудинами на 5 і на 9 літрів.

 

Розв'язання.

№ переливань	Кількість гасу після переливання
	14л	9л	5л
Початкове положення	14	0	0
1 2 3 4 5 6 7 8	5 5 10 10 1 1 6 6	9 4 4 0 9 8 8 3	0 5 0 4 4 5 0 5

Задача 2. Як, маючи лише два відра на 10 літрів і 7 літрів, принести з річки 8 літрів води?

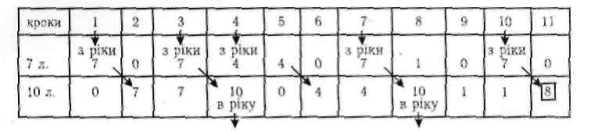
Хід міркувань при розв'язуванні способом «з кінця» можна продемонструвати на розв'язанні задачі 3.

Задача 3 Чи можна, маючи посудини на 3 л і 5 л, набрати з річки 4 л води?

Розв'язання. Припустимо, що в 5-ти літрову посудину набрано 4 л води. Це можливо, якщо з неї відлити до 3-й літрової посудини 1 л води. Для цього необхідно, щоб у 3-й літровій посудині було 2 л води. Два літри води можна налити в 3-й літрову посудину, якщо набрати повну 5-ти літрову, перелити з неї в 3-й літрову 3 л води, вилити їх у річку, а в 3-й літрову посудину перелити решту 2 л із 5-ти літрової посудини. Отже, можна набрати 4 л води, маючи 3-й літрову і 5-ти літрову посудини.

Алгоритм розв'язку задачі можна записати при допомозі пар чисел, де на першому місці вказано кількість води в 5-ти літровій посудині, а на другому місці — в 3-й літровій посудині:

(5; 0); (2; 3); (2; 0); (0; 2); (5; 2); (4; 3).

Задача 4. Як поділити порівну 12 л хлібного квасу із 12-ти літрової банки, маючи посудини на 3 і 8 л?

Задача 5. Каністра ємністю 10 л наповнена гасом. Як, маючи порожні посудини на 7 і 2 л, розлити гас у дві каністри по 5 л?

Задача 6. Є дві посудини на 9 і 4 л. Як з їх допомогою набрати з бака 6 л деякої рідини?

Задача 7. Як маючи дві посудини ємністю 5 і 9 л, набрати з озера 3 літри води?

Задача 8. Є три посудини ємністю 8, 5 і 3 л. Перша з них наповнена молоком. Як розлити в них молоко по 4 літри?

Задача 9. Як маючи лише дві посудини ємністю 4 і 9 л, набрати з річки 3 літри води?

Задача 10. Як, маючи лише дві посудини ємністю 5 і 7 л, розлити з каністри на

12 л бензин у баки двох автомобілів порівну?

    Задача 11. Як, маючи два відра на 4 і 9 л, принести з річки 7 л води?

Задача 12*. Як з повної каністри на 12 л відлити 7 л, користуючись двома порожніми посудинами на 4 і 9 літрів?

Задача 13*. У бочці є не менше 10 л бензину. Як набрати з неї 6 л з допомогою двох відер на 9 і 5 л?

Задача 14*. У бочці є не менше 13 відер бензину. Як відлити з неї 8 відер з допомогою 9-відерної і 5-відерної бочок?

 

Заняття 13-14

Тема. «Рятівні круги» великого Ейлера

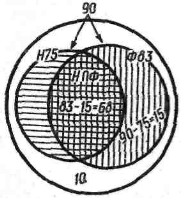Задача. Приїхало  100 туристів. З них 10 осіб не знали ні німецької мови, ні французької, 75 осіб знали німецьку мову і 83 знали французьку. Скільки туристів знали дві мови: німецьку і французьку?

Розв'язувати такі задачі допомагають такі звані круги Ейлера, які відкрив 200 років тому видатний математик, член Петербурзької Академії Наук, сучасник Ломоносова - Леонард Ейлер (1707—1783),] Це - малюнки, що є ніби «рятівним поясом» для розв'язання таких задач. Англійський математик Венн замість кру­гів брав фігури довільного контура (що не має принци­пового значення). Тому в ма­тематиці такі малюнки нази­вають діаграмами           Мал.. 1              Ейлера — Венна.

 «Помістимо» всіх туристів у великий круг (мал.1) Накреслимо в цьому крузі два менших. В один «помі­стимо»    множину   туристів,

    

 

 

 

 

 

 

 

 

 

 

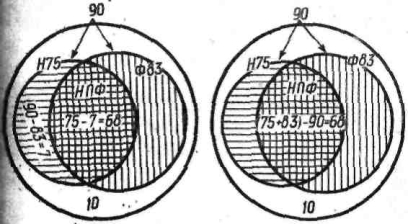
                       Мал. 2    Мал. 3

 

що знають німецьку мову, — Н, в другий—тих, що зна­ть французьку, — Ф. Ці дві множини перетинаються, і наше завдання — визначити їх переріз: Н ∩ Ф. Це можна зробити по-різному, але спочатку виключимо 10 туристів, які не знають жодної з двох мов.

Спосіб   І.   У двох  внутрішніх  кругах разом 90 чол. (100—10). Але з них 75 належать до   круга —Н, отже, решта   15 чол.   (90 — 75) знають лише французьку  мову і не входять до круга Н,  а 68 (83—15) з круга Ф входять також до круга Н, тобто Н ∩ Ф має 68 елементів. 2-й варіант цього способу; 1) 90 — 83 = 7;

2) 75 — 7 = 68 (мал. 2).

Спосіб II. 1) 90—75=15 (не знали німецької мови); І) 90 — 83 = 7 (не знали французької мови); 3) 90 — (15 + 7) = 68  (знали обидві мови).

Спосіб III. Коли б круги Н і Ф не мали спільних еле­ментів, то множина

Н U Ф містила б 75 + 83 = 158 елементів. Але за умовою їх лише 90. Отже, спільних еле­ментів буде: (75 + 83) — 90 = 68 (мал. 3).

Зобразіть розв'язання задачі способом II за допомогою діаграми Ейлера—Венна.

 Контрольні задачі

Розв'яжіть різними способами, скориставшись діаграмами Ейлера — Венна:

    1. У класі 35 учнів. З них 20 працюють у математичному гуртку, 11 — у гуртку «Умілі руки», 10 не беруть участі в роботі цих гуртків. Скільки учнів працюють в обох гуртках? Скільки учнів працюють тільки в математичному гуртку? Скільки учнів відвідують тільки один  якийсь гурток?

2. У  таборі 70 дітей, 3 них 27 відві­дують драматичний гурток,

32 — хоровий і 22 — спортив­ний. У драмгуртку 10 хористів, у хорі 6 спортсменів, у драмгуртку 8 спортсменів. 3 спортсмени відвідують драмгурток і хор. Скільки дітей не співає в хорі, не за­хоплюється спортом і не працює в драмгуртку? Скільки дітей захоплюються тільки спортом?

Заняття 15-18

Тема. Задачі, які розв'язуються з кінця.

I. Мотивація навчальної діяльності.

Розв'язати задачу:

Зустрілися дві жінки. Одна ішла на базар, а друга з базару. Перша спитала другу: «Що ти продавала?» Відповідь була така: «Я продавала яйця. Першому покупцю я продала половину всіх яєць і ще пів'яйця. Другому продала половину остачі і ще пів'яйця. Третьому я продала ще половину остачі і пів'яйця. Більше яєць у мене не було». Скільки яєць продала жінка?

(Учні шукають шляхи розв'язування задачі, при цьому виникають значні труднощі.)

II. Пояснення вчителя.

Ця задача, на перший погляд, досить складна, бо приводить до рівняння, яке учні ще не вміють розв'язувати.

Якщо аналізувати задачу «з кінця», то можна прийти до висновку, що пів'яйця стано­вить другу половину покупки третього покупця. Отже, третій покупець купив одне яйце, яке без пів'яйця становить половину остачі після продажу яєць першому покупцю. Отже, другий покупець купив 1,5 + 0,5 = 2 яйця. Аналогічними міркуваннями приходимо до висновку, що перший покупець купив 3,5 + 0,5 = 4 яйця. Отже, всього було 7 яєць.

Це розв'язання зручно подати у вигляді таблички.

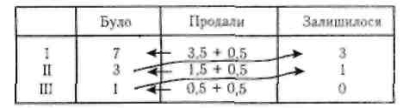
III. Осмислення вивченого матеріалу.

Задача 1. (Самостійно)

Я задумав число, додав до нього 1, суму помножив на 2, добуток поділив на 3 і відняв від результату 4. Одержав 5. Яке число я задумав?

(Розв'язання: (5 + 4) х 3 : 2 - 1 = 12,5).

Задача 2. З ящика взяли половину всіх яблук і ще пів'яблука, а потім половину залишку і ще пів'яблука, накінець, половину остачі і пів'яблука. Після цього в ящику залишилося 31 яблуко. Скільки яблук було в ящику спочатку? (З бали)

Розв'язання:

 

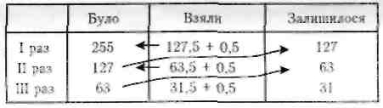
IV. Математична гімнастика.

1. Усний рахунок:

32 х 38; 81 х 89; 54 х 56; 66 х 64.

2. Математичний фокус.
(Відгадування дати дня народження)

V. Розв'язування задач.

Задача 1. Мати для трьох синів залишила зранку тарілку слив, а сама пішла на
роботу. Першим прокинувся старший син. Побачивши на столі сливи, він з'їв їх
третю частину. Другим прокинувся середній. Думаючи, що його брати ще не їли
слив, він з'їв третю частину того, що було на тарілці. Найпізніше встав молодший
син. Побачивши сливи, він вирішив, що його брати ще не їли їх, і тому з'їв лише
третю частину слив, які лежали на тарілці, після чого на тарілці залишилось
8 слив. Скільки всього слив було спочатку? 

Задача 2. Біля мосту через річку зустрілися ледар і чорт. Ледар поскаржився
на свою бідність. У відповідь чорт запропонував: «Я можу допомогти тобі. Кожного
разу, як ти перейдеш цей міст, у тебе гроші подвояться. Але кожного разу, перейшовши міст, ти повинен віддати мені 24 коп. Три рази проходив ледар міст, а коли заглянув у гаманець, там стало порожньо. Скільки грошей було у ледаря?             

Задача 3. Поверхня ставка поступово заростає лататтям. Латаття ростуть настільки швидко, що за кожен день заросла ними площа подвоюється. Вся поверхня ставка заросла за ЗО днів. За скільки днів перша половина всієї поверхні ставка була закрита лататтям?             

Задача 4. Один біолог відкрив цікаву різноманітність амеб. Кожна з них через хвилину ділиться на дві. У пробірку біолог кладе одну амебу, і рівно через годину вся пробірка виявляється заповненою амебами. Скільки потрібно часу, щоб вся пробірка заповнилась амебами, якщо в неї покласти спочатку не одну амебу, а дві?

Задача 5. Мати купила яблука. Два з них взяла собі, а решту розділила між трьома своїми синами. Першому вона дала половину всіх яблук і половину яблука, другому — половину остачі і ще пів'яблука, третьому — половину нової остачі і пів'яблука, яке залишилося.

При цьому не довелось розрізувати жодного яблука. Скільки яблук купила мама? Скільки яблук отримав кожний із синів?

 

Заняття 19-23

Тема: Розв’язування старовинних задач

Старовинний спосіб розв’язання задач на змішення сумішей

1. Як змішати масла?

     У деякого чоловіка були  продажні масла: одне ціною 10 гривень за відро, друге 6 гривень за відро. Захотілось йому зробити з цих двох масел, змішавши їх, масло ціною 7 гривень за відро. Які частини цих двох масел треба взяти, щоб отримати відро масла ціною 7 гривень?.

    Наведемо старовинний спосіб розв’язання цієї задачі.

    Один під одним пишеться ціна даних масел, зліва від них і приблизно посередині – ціна масла, яке повинно бути після змішення. З’єднавши написані числа лініями, отримаємо такий малюнок:

 6

               7

 10

Меншу частину віднімаємо від ціни змішаного масла і результат поставимо справа від більшої ціни. Потім з більшої ціни віднімаємо ціну змішаного масла, а те, що залишиться, напишемо з права від меншої ціни. Отримаємо такий малюнок.

6. 3

                7

  10    1

 

З цього робиться висновок, що дешевшого масла треба взяти втричі більше, ніж дорожчого, тобто для отримання 1 відра масла ціною 7 грн. треба взяти дорожчого масла ¼ відра, а дешевшого ¾ відра.

Чи вірно знайдена відповідь до задачі?

2. Про сплав срібла.

Маємо срібло: одне одинадцятої проби, друге чотирнадцятої проби. Скільки якого срібла треба взяти, щоб отримати 1 фунт срібла дванадцятої проби?

(В Росії існувала золотникова система позначення проби на основі російського фунту, включаючого 96 золотників, по яких проба виражалася ваговою кількістю благородного металу в 96 одиницях сплаву, наприклад, слова «срібло одинадцятої проби» означають, що в 96 частинах сплаву існує 11 частин срібла. В наш час проба означає число частин благородного металу в 1000 частинах (по масі) сплаву.)

Розв’яжіть цю задачу тим же способом, що й попередню.

3. Як змішати чай?

Дехто має чай трьох сортів – цейлонський по 5 гривень за фунт, індійський по 8 грн. за фунт та китайський по 12 грн. за фунт. В яких долях треба змішати ці три сорти, щоб отримати чай ціною в 6 грн. за фунт?

Ось розв’язання з «Арифметики» Л.Ф. Магницького:

«А когда случится мешати три товара из них же зделати четвертый по желаемой цене и тогда един перечень малейший дважды в правиле полагается. Яко же зде видимо есть»:

 5   6  6

          6

 12   1  2

           _____

 5   2  8

         6      1

 8   1  1  

              10

Тут пропонується взяти 6+2=8 частин чаю ціною по 5 грн. і по одній частині чаю ціною 8 грн. і 12 грн. за один фунт. Указаний Л.Ф. Магницьким спосіб полягає в наступному. Потрібно метод, показаний в задачі 1, застосувати двічі: перший раз, взявши речі з найменшою і найбільшою ціною, а в другий раз взявши речі з найменшою і середньою ціною. При цьому будуть знайдені долі, в яких треба змішувати речі найбільшої і середньої ціни (в наведеному прикладі 1 і 1). Склавши потім долі дешевих речей, знайдених в перший і другий раз (6+2)=8, отримаємо долю дешевої речовини в загальній суміші. Чи вірно знайдена відповідь задачі?

4. Срібло трьох сортів.

    Дехто має серебро різних проб: одне – дванадцятої, друге – десятої проби, третє – шостої проби. Скільки якого серебра треба взяти, щоб отримати 1 фунт серебра дев’ятої проби? Рішіть цю задачу способом, приведеним в задачі 3.

 

Заняття 24-28

Тема: Розв'язування логічних задач

На відміну від звичайних математичних задач чисто логічні задачі розв’язуються зіставленням фактів, зв’язки між якими далеко не завжди очевидні. Прихованість зв’язків створює враження, ніби поданої в умові задачі інформації недостатньо.

Часто в умові логічної задачі так багато фактів, що утримати їх у пам’яті важко. Тоді виконують допоміжні записи на спеціальних таблицях. Ці записи дають змогу виключити з розгляду неможливі варіанти (які суперечать умові). У відповідні клітки заносять цифри, що показують на підставі якої умови виключено ту чи іншу можливість.

Пояснимо методику такого розв’язування задач на прикладі: «Вздовж алеї, що йде в меридіональному напрямку, ростуть вишня, груша, горіх, персикове дерево, слива та яблуня. Відомо, що яблуня міститься на північ від груші, але на південь від горіха. Груша росте поруч із сливою, а горіх – поруч з персиковим деревом. Між вишнею і персиковим деревом є ще одне дерево, а між яблунею і персиковим деревом – два дерева; стільки ж дерев між грушею і вишнею. В якому порядку ростуть дерева?»

Розмістити 6 дерев уздовж алеї можна 6!¹, тобто 720 способами. Перевіряти всі ці варіанти було б занадто довго.

Пронумеруємо місця дерев з півночі на південь: 1,2,3,4,5,6. За першою умовою яблуня не на першому місці, бо вона росте на південь від горіха. Вона не може бути і на шостому місці, бо міститься на північ від груші. Отже, груша не може бути ні на першому, ні на другому місцях. Оскільки горіх росте на північ від яблуні, він не може бути ні на шостому, ні на п’ятому місцях.

Таблиця 1

	1	2	3	4	5	6
В.	3					3
Гр.	1	1
Гор.					1	1
П.			3	3		2
С.	2
Я.	1					1

 

¹n! = 1·2·3· ……..· n.

Груша росте поруч із сливою, отже, вона не може бути на першому місці. Оскільки горіх росте поруч з персиковим деревом, персикове дерево не може бути шостим. Між яблунею і персиковим деревом ростуть два дерева, тому персикове дерево не може бути ні на третьому, ні на четвертому місцях. За тією ж умовою вишня не може бути ні на першому, ні на шостому місцях.

Все це внесено в таблицю 1.

Після заповнення таблиці виявляється, що на першому місці росте або горіх, або персикове дерево.

Якщо горіх на першому місці, то персикове дерево на другому. Отже, вишня на четвертому місці, а яблуня на п’ятому. Для груші і сливи лишилися третє і шосте місця. А за умовою ці дерева ростуть поруч. Отже, горіх росте не на першому місці, тому на першому місці може бути тільки персикове дерево.

Тоді на другому місці горіх, вишня на третьому, яблуня на четвертому, груша на шостому і слива на п’ятому. Всі умови здійснено. Таблиця допомагає розв’язанню, але не доводить його до кінця. Після заповнення таблиці треба проаналізувати здобуті дані.

У деяких випадках можна обійтися і без таблиці. Це буває тоді, коли умова містить мало фактів або коли відповідь на поставлене запитання можна дістати внаслідок деяких обчислень. Наприклад, розглянемо задачу:

«Під час прогулянки у вихідний день Варський випив 1 склянку води, Алімов – 2 склянки, Павлов – 3, Шилюк – 4; Клавдія випила води стільки ж, скільки її чоловік, Ганна вдвічі більше, Олена – втричі більше, Софія в 4 рази більше за свого чоловіка. Всього ці 4 подружжя випили 32 склянки води. Хто з ким одружений?»

Чоловіки випили 1+2+3+4 = 10 склянок води, а жінки 32-10 = 22 склянки. За умовою задачі найбільша кількість води, яку могли випити жінки, дорівнює 1·1+2·2+3·3+4·4 = 30. Насправді ж випито на 8 склянок менше.

Легко помітити, що переставляння коефіцієнтів двох сусідніх множників зменшує загальну суму на 1, переставляння коефіцієнтів через 1 зменшує загальну суму на 4, а переставляння крайніх коефіцієнтів зменшує суму на 9. Отже, зменшення суми на 8 можна досягти переставлянням коефіцієнтів І і ІІІ, ІІ і ІV. Справді,

1·3+2·4+3·1+4·2 = 22 (склянки)

Отже, Варський одружений з Оленою, Алімов – з Софією, Павлов – з Клавдією, Шилюк  - з Ганною.

Тренувальні вправи

№1. Зустрілися три подруги: Бєлова, Краснова і Чернова. На одній із них була чорна сукня, на другій – червона, а на третій – біла. Дівчина в білій сукні каже Черновій: «Нам необхідно обмінятися сукнями, бо їх колір не відповідає нашим прізвищам» Який колір сукні в кожної дівчини?

№2. Микола, Борис, Вова і Юра посіли перші чотири місця у змаганнях. На питання, які місця вони посіли, троє з них відповіли:

1. Микола не перше і не четверте;
2. Борис – друге;
3. Вова не був останнім.

Хто яке місце посів у цьому змаганні?

№3. У кафе зустрілося троє друзів: скульптор Бєлов, скрипаль Чернов і художник Рижов. «Чудово, що в одного з нас біле волосся, у другого чорне, а у третього руде. Але ні у кого колір волосся не відповідає прізвищу», - зауважив чорноволосий. «Твоя правда», - відповів Бєлов. Який колір волосся в художника?

№4. У пляшці, склянці, глечику і банці знаходиться молоко, лимонад, квас і вода. Відомо, що вода і молоко не в пляшці, посудина з лимонадом стоїть між глечиком і посудиною з квасом, у банці – не лимонад і не вода. Склянка стоїть біля банки і посудини з молоком. У чому знаходиться кожна рідина?

№5. Іван, Петро, Сашко і Микола мають прізвища, що починаються літерами І, П, С, М. Відомо, що:

1. Іван та С. – відмінники;
2. Петро та І. – трієчники;
3. І. вище від П. за зростом;
4. Микола за зростом нижче від П.;
5. Сашко і Петро однакового зросту.

На яку літеру починаються прізвища кожного з хлопчиків?

№6. У лісі проводилися змагання з бігу. Обговорюючи його підсумки, одна білка сказала: «Перше місце посів заєць, а другою була лисиця». На що інша білка заперечила: «Заєць посів друге місце, а першим був лось». Пугач на все це зауважив, що у висловлюванні кожної білки одна частина правдива, а інша – ні. Хто посів перше, а хто друге у змаганнях?

Заняття 29-33

Тема: Розв’язування олімпіадних задач

№1. 10 склянок стоять на стійці, як показано на рисунку. Три містять яблучний сік (світлого кольору) та дві – виноградний сік (більше темного кольору). Сік треба перелити в п’ять склянок, що стоять праворуч а п’ять ліворуч повинні бути порожніми. Крім того, дві склянки однієї і тієї ж форми містять завжди один і то й же вид фруктового соку. Можна переливати з однієї склянки в іншу, після чого порожню склянку ставити на попереднє місце. Скільки мінімально треба зробити таких переливань, щоб отримати необхідний результат?

 

 

1         2       3          4           5         6           7        8          9         10

Розв’язання

Занумеруємо склянки зліва направо (див. рисунок). Після переливань у п’яти склянках праворуч має міститися увесь сік: виноградний у склянках одного виду, а яблучний – іншого. З п’яти склянок праворуч дві однакової форми, а три – іншої; виноградного соку вистачить лише на дві склянки, а яблучного – на три, очевидно, що виноградний сік має міститися в сьомій та дев’ятій склянках, тому першим переливанням ми маємо перелити сік з десятої склянки в дев’яту, ще три переливання будуть потрібні для переливання яблучного соку з 2,3,5 у 6,8,10.

Відповідь: 4 переливання.

 

№2. Три жабки-стрекотушки та прекрасний принц.

Еллані, Жеральдіна та Мелані говорять.

Ж: Я не знайшла прекрасного принца.

Е: Я також не знайшла прекрасного принца.

М: Еллані бреше.

Ж: Мелані говорить правду.

Лише одна з трьох жабок обманює і лише одна дійсно знайшла принца. Хто знайшов принца?

Розв’язання. Нехай бреше Жеральдіна, тоді, судячи з її слів, Мелані має також обманювати, а це суперечить умові. Отже, Жеральдіна говорить правду, з її слів випливає, що вона не знайшла прекрасного принца. Мелані говорить правду. Зі слів Мелані випливає, що Еллані – брехуха, а отже, Еллані знайшла прекрасного принца.

Відповідь: Еллані знайшла прекрасного принца.

 

№3. В обох випадках терези перебувають у рівновазі. Яка вага одного яблука?

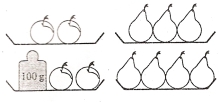
Розв’язання. Два яблука важать як три груші, тому, якщо з терезів зображених на рисунку, забрати 2 яблука та 3 груші, рівновага не порушиться, отже, вага однієї груші 100 г, трьох груш – 300 г, двох яблук – 300 г, одного яблука – 150 г

Відповідь: 150 г.

 

№4. Розмістіть п’ять доміно, що задано умовою, у фігурі. Домалюйте необхідні частини доміно.

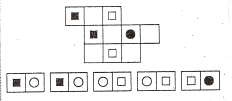
Розв’язання. Крайня ліворуч та крайня праворуч клітинки можуть бути розміщені в доміно лише одним способом (див. рис. 1).

 

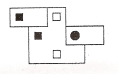
        Рис.1

Тепер, очевидно, існує один спосіб розміщення цих доміно (див. рис. 2).

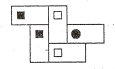
        Рис.2

За умовою, на доміно із замальованим колом знаходиться прямокутник, із замальованим прямокутником – коло, а з прямокутником - коло (див. рис. 3).

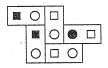
       Рис.3

 

№5. Дідусь Михайло поділив квадрат на п’ять однакових прямокутників так, як показано на рисунку. Знайдіть периметр квадрата, якщо периметр кожного з п’яти однакових прямокутників дорівнює 150 м.

Розв’язання.

Р( АВВ₁А₁) = 2(АВ+АА₁)=150 см,

АА₁=AF=AB+BC+CD+DE+EF=5AB, 

AB =

  A B C D E F

A ₁B₁C₁D₁E₁F₁

12 AA₁ = 750,

AA₁ = 62,5 см.

Р(AFF₁A₁) = 62,5·4 = 250 cм.

Відповідь: 250 см.

 

№6. Невмілий друкар. Коли друкар хотів занумерувати сторінки з першої і до останньої, не пропускаючи жодної, він припустився помилки. Замість 9 він завжди друкував 6, а інші цифри були надруковані правильно. Для нумерації всіх сторінок було використано рівно 36 разів цифру 6. Скільки сторінок містить книги?

Розв’язання. На кожних десяти сторінках книги цифра 6 зустрічається двічі в розряді одиниць. Тому з 1 по 59 сторінки шістка зустрічається 12 разів, з 60 по 69 вона з’явиться також 12 разів (двічі в розряді одиниць та 10 разів у розряді десятків). З 70 по 89 цифра 6 зустрічається 4 рази.

Отже, з 1 по 89 сторінку шістка зустрічається 28 разів, 8 шісток, що залишилися, зустрінуться з 90 по 97 сторінки.

Відповідь: У книзі 97 сторінок.

 

Заняття 34-35

Тема: Математичні цікавинки

Гра «Подорож по маршруту в Країну Знань»

1. Ми в аеропорту «Не зіб’юсь з дороги». Лічіть до 40, але замість чисел, які діляться на 4, говоріть «Не зіб’юсь». Отже, добре пригадайте таблицю множення на 4. (Діти по черзі лічать: один, два, три, не зіб’юсь, п’ять, шість, сім, не зіб’юсь і т.д.).

2. Наш літак приземлився на аеродромі «Кмітливість». Тут нам пропонують задачу: «Книжка коштує 20 коп. та ще половину своєї ціни. Скільки коштує книжка?» Розв’язуйте швидко, зупинка літака – 3 хв.

(З’ясувавши, що книжка коштує 40 коп., учитель продовжує вести учнів обраним маршрутом).

3. А тепер нас просять допомогти метеорологи, яким треба уточнити графік роботи літаків. Нас запитують: «Якщо о 12 год дня йде дощ, то чи можна сподіватися, що через 36 год буде сонячна погода? (ні, бо це буде ніч).

4. Ми знову в дорозі – поспішаємо, щоб не запізнитися в Країну Знань. Але нас не випустять з літака просто так. Перепусткою до Країни Знань є відповідь на запитання: «Коли ми дивимося на цифру 2, а кажемо 10?».

З’ясувавши відповідь (коли годинник показує 10 хвилин якоїсь години), учитель повідомляє, що всі діти одержали перепустку до Країни Знань.

Калейдоскоп часу

Вузлик на пам’ять

Усі знають, що в лютому 28 або 29 днів. А от які місяці мають по 30 днів, а які по 31 дню? Звичайно, можна полічити по кісточках на руках. Але це досить незручно. Краще запам’ятати, що по 30 днів мають лише чотири місяці, порядкові номери яких римськими цифрами записуються так, що їх дуже легко запам’ятати:

IV і VI (квітень і червень);

IX і XI (вересень і листопад).

Загадки-жарти

1. В якому місяці діти найменше плачуть?

Відповідь: у лютому.

2. Коли година має менше від 60 хвилин?

Відповідь: Коли вона академічна (урок триває 45 хв).

3. Коли дід буде молодший за онука?

У літаку, що прямував до Країни Знань, було два пасажири: дід і онук. Цікава парочка! Уявіть собі, онук щоразу старіє в кілька разів швидше, ніж дід. І як це в нього виходить? Не розумію! 40 років назад дід був старший за онука в 10 раз, а зараз він старший за онука тільки в 2 рази. Мабуть скоро їх вік зрівняється? А потім дід стане молодший за онука!?

Чи можна дізнатися, коли дід стане вдвоє молодший за онука?

4. Назвіть підряд 5 днів тижня, не використовуючи назв днів і порядкових чисел.

Відповідь: Позавчора, вчора, сьогодні, завтра, післязавтра.

5. Мій дід старший за мого батька на 24 роки, а мій батько на стільки ж старший за мене. Скільки років кожному в нас, якщо 2 роки тому нам разом не було й 100 років?

Відповідь: 11, 35, 59.

6. За який час можна найшвидше підсмажити 3 скибочки хліба на сковорідці, яка вміщує лише дві скибочки, якщо на підсмажування однієї скибочки з одного боку потрібно 1 хв?

Відповідь: за 3 хв.

7. Один учень розв’язав задачу за 1 год. Який час розв’яжуть цю задачу 10 учнів?

8. 10 насосів за 10 хв викачують 10 т води. За скільки хвилин 25 насосів викачають 25 т води?

Відповідь: за 10 хв.

Література:

1. Аменицкий Н.Н., Сахаров И.П. Забавная арифметика. – М.: Наука. Физмат-лит. 1991.
2. Гєнкін С.А., Ітенберг І.В, Фомін Д.В. Ленінградські математичні гуртки. – ТВіМС, 1997.
3. Кушнір І. Шедеври шкільної математики. – К: ООО «Астарта», 1995.
4. Математика в школах України.  Науково-матеодичний журнал: №№31, 33, 2008, №2,4, 2009
5. Олейник С.Н., Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи. – М.: наука. Физмат.лит., 1988.