ЦІКАВА МАТЕМАТИКА У РОЗВЯЗКАХ І МІРКУВАННЯХ ЯК ШЛЯХ ДО РОЗВИТКУ ТВОРЧОГО МИСЛЕННЯ УЧНІВ

Робота з обдарованими дітьми

Вчитель математики Луньова Ірини Ярославівни вища категорія,  вчитель методист

                                             Анотація

Навчально-методичний посібник розроблено для підготовки учнів 5-11 класів до математичних конкурсів, олімпіад, турнірів. Ця розробка адресована тим, хто хоче навчитися розв’язувати задачі олімпіадної математики та навчити цього своїх учнів. Вона написана на основі багаторічного досвіду підготовки учнів до участі в міських і обласних математичних олімпіадах та конкурсах.

Мета цієї розробки – надати вчителям, учням конкретну допомогу в розвитку вміння розв’язувати задачі даного напрямку.

В посібнику пропонуються програми та нестандартні завдання, які  поліпшують якість знань, розвивають пізнавальну діяльність та творчу ініціативу дітей. Використання таких вправ сприятиме вихованню в учнів інтересу до вивчення математики, розвитку інтелектуальних здібностей та відкриттю творчого потенціалу школярів.

Сподіваюся, що матеріали збірки Ви, шановні колеги, будете використовувати не тільки на шкільних олімпіадах, турнірах, позакласних заходах , але й на щоденних уроках математики. Адже, як казав великий А. Ейнштейн, «вміє вчити той, хто вчить цікаво».

                                    

   Будь якому суспільству потрібні обдаровані люди і завдання суспільства полягає в тому, щоб розглянути і розвинути здібності всіх його представників. На превеликий жаль далеко не кожна людина здатна реалізувати свої здібності. Проте розвиток здібностей і талантів будь-якої людини важливо не тільки для нього самого, а й для суспільства в цілому. Якісний стрибок у розвитку нових технологій спричинив за собою різке зростання потреби в людях, що володіють нестандартним мисленням, що вносять новий зміст у виробниче і соціальне життя,вміють ставити і вирішувати нові завдання пов’язані з майбутнім. Жага відкриття, прагнення проникнути в найпотаємніші таємниці буття народжується ще на шкільній лаві. Вже в початковій школі можна зустріти таких учнів, яких не задовольняє просто робота зі шкільним підручником. Такі діти явно або не явно виділяються серед своїх однолітків своєю здатністю вчитися, придумувати незвичайне, вирішувати нестандартні завдання. Тому вчителі повинні піклуватися про задоволення інтелектуальних та творчих запитів цих учнів . Розвиток логічного мислення – одне з основних завдань вивчення математики. Яку б професію в майбутньому не обрав би мій учень, йому потрібно з шкільної парти навчитися правильно і швидко міркувати, аргументувати розв’язання задач та отриманий результат, формулювати задачі і творчо підходити до їх вирішення, самостійно поповнювати багаж знань. Як відомо, інтерес до математики і математичні здібності виявляються в ранньому віці. Значну роль у їх розвитку відіграє систематичне розв’язування задач, які можуть захопити юних математиків  і породжувати прагнення до самостійних досліджень. Запропонована програма і задачі є доповненням до окремих тем шкільного курсу.                                                                                                           

                                        

 

Логічні задачі, як шлях до творчого розвитку мислення учнів

 

Сучасна школа вимагає переосмислення процесів навчання і виховання, застосування перспективних технологій, створення умов для самонавчання, саморозвитку і самореалізації особистості учня. На перший план виступає розвиток творчого потенціалу дитини, розкриття індивідуальних, самобутніх її здібностей.

Важливим засобом інтелектуального розвитку школярів є використання на уроках математики завдань з логічним навантаженням. До таких завдань відносяться ті завдання, у яких зв’язки між даними і шуканими висловлено нечітко. Тому в процесі роботи необхідно розкрити і встановити існуючі зв’язки. Успішне розв’язання зазначених завдань залежить від уміння учня логічно і творчо мислити, бути кмітливим, здатності вести цілеспрямований пошук плану, будувати складні судження – міркування зі сполучниками: і, чи, якщо…, то. Зміст кожного завдання з логічним навантаженням дає змогу учням включати в пошук розв’язання дотепні міркування і певне розмірковування, цілісно і синтетично уявити і, завдяки цьому, глибоко вникнути в ситуацію, спланувати свої дії на три-чотири кроки вперед, передбачити результат (навіть негативний) і на основі цих міркувань вибрати ланцюжок дій, який найбільш швидко та економно приведе до очікуваного результату. Процес розв’язування завдань з логічним навантаженням має такі етапи: 

         - Підготовчий – уміння аналізувати структуру завдання, зіставляти дане завдання з відомими.

        - Визрівання нової ідеї, формулювання гіпотези (передбачення) – уміння знаходити приховані зв’язки між даними і невідомими елементами.

       -  Перевірка гіпотези – уміння аналізувати гіпотезу щодо можливого розв’язання завдання.

            - Розвиток ідеї – уміння логічно опрацьовувати знайдене розв’язання завдання.

Провідною метою використання завдань з логічним навантаженням на уроках математики є інтелектуальний розвиток кожного учня, який включає:

1. Оволодіння загальними розумовими діями і прийомами розумової діяльності: аналізом, порівнянням, узагальненням, аналогією.

2. Розвиток пізнавальних інтересів: пам’яті, уваги, уяви й, особливо, діалектичного мислення, що досягається поступово шляхом підведення учнів до більш складних узагальнень.

3. Мовний розвиток учнів, який здійснюється у процесі проблемно-пошукового діалогу між учителем та учнями через пояснення власної точки зору, зіставлення різних поглядів, висування припущень, їх аргументація, висловлення оцінних суджень.

         Логічні задачі  не мають прямого зв’язку з яким-небудь учбовим матеріалом, тому їх можна використовувати в будь-якій темі курсу математики з метою виховання в учнів уміння проводити доказові міркування. Наприклад. Вовк і лисиця змагалися з бігу. Хто яке місце зайняв, якщо відомо, що Вовк був одним із перших, а Лисиця була передостанньою. Відповідь: Лисиця – перша Вовк – другий. Тут учні мають усвідомити, що за умовою задачі є тільки двоє звірів, і Лисиця прибігла передостанньою, тобто першою.

Розв’язування завдань з логічним навантаженням створює чудові можливості для прояву ініціативи і самостійності учнів, розвитку їх творчого потенціалу. Виконання цікавих завдань дає і велике задоволення.

Розвиток навичок розв'язування задач, безумовно, сприяє підвищенню рівня інтелекту, а під час дозвілля - це дуже корисне тренування.  Головна цінність цих завдань полягає в тому, що дитина впевненіше підходить до розв'язування власних особистісних проблем, а не тільки цікавих головоломок. Адже одні й другі мають багато спільного, зокрема методи розв'язування задач. І там, і тут можна досягти значних успіхів шляхом вправляння й тренування. Читаючи задачу, учень застосовує всю свою спостережливість і вміння зосередитися, відбирає з неї ті факти, які потрібні для розв'язування. Тому майже на кожному уроці пропоную учням такого типу вправу. Так у 5 класі під час вивчення теми  «Розв’язування задач за допомогою рівнянь» учнями було  розв’язано їх декілька, причому їх зміст було пов’язано з історією і літературою.  Такі задачі розвивають в дитини такі якості, як раціональність та практична кмітливість, комбінаторне мислення, вміння відшукати оптимальний шлях, продумати виграшну стратегію.

Використання таких завдань на уроках сприяє вихованню в учнів інтересу до вивчення математики, бажання пізнати нове, розширити кругозір. Разом з тим вони полегшують процес засвоєння навчального матеріалу, розвивають пізнавальну діяльність та творчу ініціативу дітей.

Оскільки нестандартних задач у підручнику небагато, то я створила підбірку логічних вправ  для 5 класу з кожної теми програмованого матеріалу. Ці завдання  можна використовувати як і на уроках, так і в індивідуальній роботі  з розвитку творчих здібностей учнів. Вони під силу не лише відмінникам з математики, а й прихильникам інших шкільних дисциплін. Логічні вправи не потребують великих затрат часу на обчислення, тому їх широко можна застосовувати в позакласній роботі з математики і не тільки в 5 класах. Вони також є першою сходинкою при підготовці дітей до участі в майбутньому в олімпіадах.

                                                                           

        Цікава математика у розв’язках  і міркуваннях

 

В таких задачах учнi не знають заздалегiдь нi способу їх розв’язання, нi того, на якому навчальному матерiалi ґрунтується розв’язання. Щоб виконати таку вправу, треба всебiчно врахувати взаємозв’язки між даним i шуканим, правильно оцiнити окремi компоненти завдання, поданого в нестандартнiй формі, зрозумiти  властивостi величин та залежностi мiж ними, якi безпосередньо не зазначенi в умовi, але випливають з певних закономірностей, причинних залежностей. Задачi логiчного спрямування стимулюють дiтей до активної розумової дiяльностi, до творчого пошуку, розвиваютъ логiчне мислення, кмiтливiсть, комбiнаторнi здiбностi, а головне — сприяють усвiдомленню математичних закономiрностей, формуванню навичок свiдомого вибору дiй, практичних умiнъ i загалом пiдвищують  культуру мислення. Досвiд показує, що сильнi учнi з iнтересом розв’язують такi задачi, виявляють творчу самостiйнiсть, насолоджуються радiстю перемоги. А емоцiї, викликанi розв’язуванням нестандартних творчих задач, пережитi людиною в шкільному вiцi, можугь пробудити у неї смак до розумової дiяльностi, залишити свiй слiд в розумі i характерi людини на довгi роки, а може бути, i на все життя.

              

Використання історичного матеріалу на уроках математики як засіб розвитку пізнавальної активності учнів

 

          Під час викладання математики зібрано певну кількість історико-математичних відомостей, пов'язаних з вивченням шкільного курсу математики, цікавих задач, задач на «кмітливість», старовинних задач, різних математичних «чудес», які використовую на уроках.

Під час вивчення теми арифметична прогресія у 9 класі розв'язуємо історичну задачу про поділ хліба .

Зазвичай, вивчаючи прогресії, розв'язують задачу двох тисячорічної давності про вина городника винахідника шахів. Але значно старша задача - це задача про поділ хліба, яку записано у знаменитому єгипетському папірусі Рінда. Цей папірус знайдений Ріндом наприкінці минулого століття, складений близько 2000 років до нашої ери і списаний з іншого, ще давнішого математичного твору, можливо третього тисячоліття до нашої ери.                                         

Задача

Сто міх хліба поділити між п'ятьма працівниками так, щоб другий одержав на стільки само більше хліба від першого, на скільки третій одержав більше другого, четвертий більше від третього, п'ятий від четвертого. Крім того, двоє перших повинні одержати хліба у 7 раз менше від інших. Скільки мір хліба треба дати кожному?

Діти також розв'язують охоче старовинні задачі з арифметики. З старовинного російського підручника з математики, який має назву «Повний курс чистої математики, складений Артилерії Штик-Юнкером і Математики партикулярним Учителем Юхимом Войтяхівським на користь і застосування юнацтва і тих, що роблять вправи з математики» (1795р.) розглядаємо таку задачу про винагороду воїнам.

Задача.Воїнові, що заслужив видано винагороду: за першу рану - 1 к., за другу - 2 к., за третю - 4 к. і т.д. Після підрахунків виявилось, що воїн одержав винагороду 655 руб. 35 к. Запитується, яка кількість його ран.

При вивченні теми « Розв'язання задач за допомогою квадратних рівнянь» у 8 класі, розв'язують таку задачу.

Задача Ейлера

Двоє селянок принесли на базар разом 100 яєць, одна більше, ніж інша. Обидві вторгували однакові суми. Перша мовила тоді другій: «Коли б у мене були твої яйця, я б вторгувала б на 15 крейцерів». Друга мовила: «А якби твої яйця були у мене , я вторгувала б на них 6 2/3 крейцера». Скільки грошей було у кожної селянки?

Зацікавлено учні сприймають віршовані задачі і короткі історичні довідки до них. Вивчаючи тему «Розв'язання задач за допомогою рівнянь» у 7 класі, розв'язуємо з учнями задачі Метродора, який увійшов в історію математики як автор цікавих задач, складених у віршованій формі. Задачі Метродора  входили до рукописних збірників і були дуже поширені. Український переклад цих задач виконав Іван Франко.

Пори дня

«О примудрий чесознавче,

Яка часть нам дня прийшла вже?»

«Що прийшло вже з сеї днини,

Візьми з того дні третини.

А на все дозвілля своє

Матимеш ще стільки вдвоє».

Застосування елементів українознавства на уроках математики нерідко дає несподівані високі результати. Математичні поняття пов'язуються в пам'яті не лише з цифрами і буквами, а ще асоціюються з історичними подіями чи предметами які їх стосуються. Застосовуючи українознавчу інформацію на неспеціальних уроках, учитель досягає водночас кількох цілей. Таке поєднання дає змогу подати учням матеріал у новому світлі, що значно підвищує їх інтерес, концентрує увагу та, відповідно, покращує процес мислення й вчення. Крім того, запровадження українознавчих елементів розвиває в учнів почуття патріотизму, допомагає глибше ознайомитися з історією, звичаями та традиціями рідного краю, духовно збагачує. Такий інтегрований підхід допомагає всесторонньо ознайомлювати учнів з досягненнями української науки, надбаннями культури українського народу.

Завдання: Розв'язати пропорції та знайти суму знайдених чисел.

•1.     х : 16 =120 : 16

•2.     х : 12 = 540 : 18

•3.     260 : 16 = 390 : х

•4.     276 : 12 = х : 55

Відповідь: 1905 - рік, коли вийшов «Словар української мови».

•1.     215 : х = 86 : 2

•2.     123 : 41 = 9 : х

•3.     310 : х = 124 : 2

•4.     361 : 19 = 57 : х

Відповідь: 16 липня 1990рік прийнято декларацію про незалежність України, де проголошено наміри народу самостійно вирішувати свою долю.                                                  

          

                                          5 клас                                                                                                             

1. Задачі на складання загадок, математичних ребусів, задачі на гру чисел, задачі записані у вигляді цікавих історій.
2. Складання та розрізування паперу, рамки та вкладки Монтессорі.
3. «Стомахіон» Архімеда. Різновид конструкторів поліміно, Т-конструктор. Шахова дошка.
4. Принцип доведення від супротивного. Поняття контра позиції, інверсії.
5. Задачі що розв’язуються з кінця.
6. Задачі на логіку.
7. Задачі на перестановку, переливання та зважування.
8. Старовинні задачі на вгадування чисел.
9. Принцип крайнього.
10. Геометричні задачі.

 

                    

 

 

                                           Задачі

1. Назви всі двоцифрові числа, сума цифр яких дорівнює три.

2. Назви всі двоцифрові числа, сума цифр яких дорівнює найбільшому одноцифровому числу.

3. Які цілі числа при закресленні останньої цифри зменшується у ціле число разів?

4. Як швидко обчислити:    1+3+5+7+9+…+99?

5. Яке число лишнє:     0, 1, 2, 3?

6. Скільки є двоцифрових чисел, у яких серед цифр є хоч одна п’ятірка?

7. Для нумерації сторінок книги необхідно всього 1392 цифри. Скільки сторінок  має ця книга?

8. Скільки всього прабабусь і прадідусів було у всіх ваших прабабусь і прадідусів?

9.   За диван заплатили спочатку 416 грн., а потім і ще половину вартості цього дивану Скільки коштує диван? 

10. Жили-були дід та баба. Була в них курочка Ряба. Курочка несе кожне друге яйце просте, а кожне третє – золоте. Чи може таке бути?

11. Візьміть будь-які три різні цифри, крім нуля. Складіть із них всі можливі трицифрові числа, додайте їх і отриману суму поділіть на суму взятих  цифр. У вас вийде 222. Чому?

12. Обчисліть: 2379•23782378 -  2378•23792379.

13. Мишці до дірки 20 кроків, кішці до мишки 5 стрибків. Доки кішка робить один стрибок, мишка робить 3 кроки, а 1 стрибок кішки дорівнює 10 крокам мишки. Чи дожене кішка мишку?

14. Поставте замість зірочок знаки + і – так, щоб виконувалась рівність: 40*20*60*30*50=100.

15. У батька 5 дочок і кожна дочка має брата. Скільки дітей у батька? (шестеро).

16. Кравець має 18м сукна і щодня відрізає від нього по 3 м. На який день від це зробить останній раз? (на п'ятий день).

17. Двоє пішли - 5 цвяхів знайшли. Четверо підуть - скільки знайдуть? (жодного).

18. Горіло 5 свічок. Дві з них згасли. Скільки свічок залишилося? (дві).

19. Одне яйце варять протягом 4 хвилин. Тоді воно вважається звареним. За скільки  хвилин можна зварити 5 яєць. (за 4 хвилини).

20. Селянин ішов до залізничної станції і зустрів дві бабусі, кожна з яких несла по два кошики і в кожному кошику було по два кролі. Скільки йшло до станції?

(один селянин).

21. Скільки буде десятків, якщо два десятки помножити на два десятки? (40).

22. На дереві сиділо 6 горобців. Стрілець вистрілив, влучив у двох із них. Скільки горобців залишилося на дереві? (жодного).

23. Два півні можуть розбудити своїм співом одну людину. Скільки людей розбудять своїм співом шість півнів?  (одну людину).

24. Що більше і на скільки: х чи х+10;  х чи х – 5?

25. Коли таке буває: 65+х=65-х,     240-х=х?

26. За записами розв’язання відтвори початкове рівняння:

…*…=30;       х=90-30;    х=60.

27. В одній купці 25-копійкові монети, а в другій – 5-копійкові. Кількість монет в купках однакова. Скільки грошей в кожній купці, якщо всього було 3 грн.?

28. Деяке число поділили на 2, до результату додали 1, потім все це поділили на 5, результат помножили на 9 і знову отримали те саме число. Знайти це число. ( 18 )

29. Знайди х, не виконуючи ніяких обчислень:        

     64-х=64+х                                                                          

     х + 341=341 - х  

30.Знайди різницю добутків чисел 809∙908  і   809∙808.

40.  Знайди значення виразів:

 а) 6х + 6у, якщо х+у=20

 б) 9х- 9у, якщо х – у =11

41. Кенгуру купив три сорти шоколадок: великі, середні, і малі. Одна велика шоколадка коштує 4 гривні, одна середня шоколадка коштує 2 гривні, малі шоколадки по одній гривні. За16 гривні Кенгуру купив 10 шоколадок. Скільки великих шоколадок купив Кенгуру? Відповідь:  1 велику, 3 середні, 6 маленькі.

42.   У якому трикутнику сума двох його кутів дорівнює третьому?

(у прямокутному).

43. Скільки граней має непідстружений шестигранний олівець?

44. Як перевірити, що чотирикутник є квадратом.

45. Маємо прямокутник зі сторонами 12см і 10 см. Що треба зробити з його довжиною, щоб отримати квадрат?

46. Як  у кімнаті можна поставити 2 стільці так, щоб біля кожної стіни стояло по одному стільцю?

47. Чи можна з трьох паличок 10, 6 і 4 см скласти трикутник? Паличкою якої довжини треба замінити меншу, щоб можна було скласти трикутник?

48. Боксерський ринг має форму квадрата, сторона якого 6м. Ринг огороджено потрійним канатом. Скільки метрів канату використали?

49. Доберіть закінчення до даних слів, яке є мірою довжини.

    Пери

     Діа                          ( . . . . )

     Моно

50.  Підберіть слово, яке означає те саме, що і слова за дужками.

Чотирикутник ( . . . . . . . ) друга степінь числа.

51.Із 22 сірників складіть прямокутник найбільшої площі.

52.Периметр прямокутника 28 см (довжини виражаються цілим числом). Чи може його площа дорівнювати 40 см2? 33см2?

53.Скільки чотирикутників у п’ятикутній  зірці?

  54.Садівника спитали, скільки у твоєму саду дерев? Він відповів: "Половина всіх моїх дерев -яблуні, половина з тих, що залишилися - груші; а решта шість дерев - вишні". Скільки в цьому саду дерев? (24 дерева).

55. Вранці бабуся поділила між чотирма внуками порівну два яблука, в обід  - шість, а ввечері – три. Скільки яблук одержав кожний онук за день?

56. Пляшка, що може вмістити 1/3 літра, заповнена на ¾ водою. Скільки води залишиться у пляшці після того, як з неї вилили 200 мл?

57.Запиши число 100 чотирма дев’ятками. ( 99 + 9/9 )

58.За тиждень Вінні - Пух з’їдає 9 кг меду. Скільки меду в середньому з’їдає Вінні - Пух за 1 день?

59 При яких значеннях х дроби: 7 /х  і х /3 одночасно неправильні?

60.При яких значеннях х дроби: х /7  і 3 /х одночасно правильні?

61.Перестав цифри різними способами так, щоб дістати неправильний дріб зі   109/110.

62.Перестав цифри різними способами так, щоб дістати правильний дріб зі   111/109.

63. У банку помістилося 1 л молока і ще могло поміститися 1/5 л. Яка місткість банки?

64. Коли до третини задуманого числа додати 5, то вийде 20. Яке число було задумано?

64. Відомо,що третина половини числа становить 12. Знайдіть це число.

65. Число 666 потрібно збільшити у півтора рази, не проводячи над цим ніяких арифметичних дій. Як це зробити?   (Аркуш паперу, на якому написано число, повернути на 180°).

66. Скільки буде, коли 10 поділити на десяту частину?  (100).

67.  Скільки буде, коли сотню поділити на четверту частину?  (400).

68. Знайди четверте число в записі: 0,3; 0,6; 1,2;…

 

69. Не обчислюючи частки, порівняй вирази:

а)20,8:16 і 10,4:8                   

б)1,365:65 і 13,65:65

 в)14,7: 21 і 1470:21

70. Який знак треба поставити між цифрами 3 і 4, щоб одержати число більше, ніж 3, але й менше, ніж 4?

71. Швидкість течії річки 1,5 км/год. Пароплав пливе проти течії річки. На скільки кілометрів за годину його швидкість за течією буде більша від швидкості проти течії?    (на 3 км/год).

72. У прикладах витерті коми. Розставте їх у потрібних місцях:

26+14=4          4+215=615         63+19=253856 - 556=3

74-36=704      89-6=29

73. Знайди пропущене число: 

2,7        6,1    3,4

1,8            5,9

74. Назви 4 числа більших від 0,1, але менших за 0,3

 

 

                   

                                6 клас

1.Задачі економічного характеру.

2.Задачі на принцип Діріхле.

3.Задачі на подільність. Теорема про подільність суми і добутку чисел.

4.Старовинні задачі на обчислення в часі та подорожі.

5.Теорема про ділення з остачею.

6. Гральний кубик.

7. Задачі про існування числа з певними властивостями.

8.Задачі на відсотки.

9.Аркуш Мебіуса.

10. Комбінаторні задачі. Біном Ньютона.

11.Задачі на періодичність повторення остач.

12. Задачі на розбиття множини натуральних чисел на підмножини відношенням: мати рівні остачі в результаті ділення на задане число.

 

                         

                                          Задачі

1. Кілька хлопчиків збирали гриби. Один знайшов 6 грибів, а всі інші по 13. Другого дня кількість хлопчиків була іншою. Один з них знайшов 5 грибів, а решта - по 10. Скільки хлопчиків було кожного разу, якщо в обох випадках вони назбирали однакову кількість грибів К, причому відомо, що 100 < К < 200?

Відповідь: першого разу було 14 хлопчиків, а другого - 18 хлопчиків.

2. Знайти всі трицифрові числа, для яких різниця між числом і потроєною сумою його цифр дорівнює 107.

Відповідь: 122 та 149.

3. Знайти всі двоцифрові числа, кожне з яких на 9 більше від суми квадратів його цифр.

Відповідь: 10, 11, 34, 74, 90, 91.

4. Довести, що довільне просте число р > 2 єдиним способом можна подати у вигляді різниці квадратів двох натуральних чисел.

5. Знайти всі пари натуральних чисел, добуток яких у р разів більший за їх суму, де р - просте число.

Відповідь:

 якщо к = 1, то х = р + 1, у = р + р2; якщо к = р, то х = 2р, у = 2р;

якщо к = р, то х = р2+р, у = 1+р.

6. Скількома способами число 1285 можна подати у вигляді суми к послідовних натуральних чисел?

Відповідь: Отже, існує 3 способи.

7. Знайти найменше натуральне число, яке під час ділення на 9 і 14 дає відповідно остачі 7 і 5.

Відповідь: 61.

8. Для настилання підлоги завширшки 6 м є дошки завширшки 17 см і 15 см. Скільки треба взяти дощок того й другого розмірів, якщо вважати, що довжина кімнати і довжина дощок однакові, і дошки кладуться вздовж кімнати?

9. На трасі 800 м треба прокласти газові труби. На складі є труби довжиною 11 м і 13 м. Як найекономніше використати ці труби?

10. Автобаза може послати 30 машин для вивозу цукрових буряків на три приймальні пункти. На базі є дво-, три- і п'ятитонні машини.

11. Скільки треба машин кожної тонажності, щоб за кожну ходку вивозити 100 тонн буряків? Знайти оптимальний розв'язок.

12. 26 осіб витратили разом 88 монет, причому кожен чоловік  витратив 6, жінка - 4, а дівчина -2 монети. Скільки було чоловіків, жінок і дівчат? (Задача Адама Різе (1492-1559)).

13. Хтось купив 30 птахів за 30 монет; з числа цих птахів: за кожних 3 горобців було заплачено 1 монету, за кожних двох горлиць також одну монету і, нарешті, за кожного голуба - по дві монети. Скільки куплено птахів кожного виду? (Задача Леонардо Пізанського (1201)).

 

                      

 

                                   7 клас

1. Задачі, що розв’язуються за допомогою таблиць істинності.
2. Алгоритм Евкліда і мала теорема Ферма.
3. Лінійні рівняння з модулями.
4. Нестандартні способи розв’язування рівнянь:

а) графічний метод;

б) використання умови існування дробу;

в) використання умови рівності дробу нулю;

г) Діафантові рівняння;

д) перетворення в добуток;

е) рівняння з параметром.

5.Задачі на роботу і продуктивність праці.

6.Задачі на відсотки:

а)на концентрацію і процентний вміст;

б)на процентний приріст і обчислення «складних відсотків».

7. Задачі на рух

8. Задачі що приводять до невизначених рівнянь.

9. Визначні точки і лінії в трикутнику.

10. Чотирикутник і коло.

              

                                 Задачі

1. Розшифрувати ребус:    К І Т 2 = З А Є Ц Ь, де різним буквам відповідають різні цифри.

Відповідь. 2092  = 43681,  2592 = 67081.

2  Якою цифрою закінчується число 220 + 211 ?

А: 0            Б: 2            В: 4           Г: 6           Д: 8

Відповідь. Цифрою 4.

3.  Який із двох виразів більший:

Відповідь: перший вираз більший.

Розв’язання. Підрахувати, який із виразів більший, можна безпосередньо, звівши обидва до спільного знаменника. А можна зробити інакше — згрупувати доданки та від’ємники в пари: 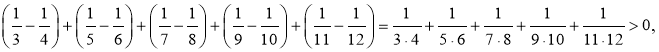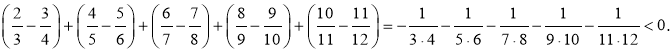Оскільки перший вираз додатний, а другий — від’ємний, перший вираз є більшим.

4. Знайдіть найменше п’ятицифрове число, яке ділиться на 9 і всі цифри якого різні.

Відповідь: 10 269.

Розв’язання. Число буде найменшим, якщо якомога меншими є його перші цифри, зокрема якщо перша цифра числа — 1, а друга цифра — 0. За умовою цифри числа не мають повторюватися, тож найменше можливе значення третьої цифри — 2. Для того, щоб число було кратним 9, треба, щоб сума двох його останніх цифр та цифр 1, 0 і 2 була кратною 9, тобто дорівнювала 9 чи 18. Це означає, що сума двох останніх цифр числа повинна дорівнювати 6 або 15. У першому випадку двома останніми цифрами можуть бути 06, 15, 24, 33, 42, 51 або 60; жодна з цих пар не дасть разом із цифрами 102 число, всі цифри якого різні. Якщо ж сума двох останніх цифр — 15, це або 69, або 78, або 87, або 96. Пара цифр 69 і дає найменше число, що задовольняє умову: 10 269.

5. Чи можна розфарбувати всі 12 частин рисунка у три кольори так, щоб жодні дві частини, пофарбовані однаково, не мали спільної межі?

Відповідь: не можна.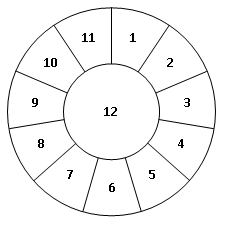

Розв’язання. Спробуємо розфарбувати рисунок у червоний, зелений та синій кольори. Центральний круг можна зафарбувати у довільний із трьох кольорів. Пофарбуймо його червоним. Усі 11 секторів мають спільну межу із центральним кругом, а отже жоден із них фарбувати у червоний колір після цього не можна.

Розглянемо перший сектор. Його слід фарбувати або в зелений, або в синій колір. Пофарбуймо його зеленим. Тоді другий сектор не може бути ні зеленим, ні червоним, тобто маємо зробити його синім. Тепер третій сектор не може бути синім і не може бути червоним, отже фарбуємо його зеленим і т. д. Вийде так, що 11-й сектор ми пофарбуємо зеленим кольором. Але тоді сусідні 1-й та 11-й сектори матимуть однакові кольори. Отже, розфарбувати рисунок потрібним чином не вдасться.

6. Сторони чотирикутника ABCD мають такі довжини: АВ=9, ВС=2,СD=14, АD=5 . Знайдіть довжину діагоналі AC, якщо відомо, що вона є цілим числом.

Відповідь:  АС=10

Розв’язання. Застосуймо нерівність трикутника до   та до  : для першого матимемо, що  , тобто що  , а для другого трикутника — що  , тобто  . Таким чином,  , звідки 

Зауважимо, що чотирикутник, описаний в умові задачі, нескладно сконструювати. З допомогою тригонометрії можна показати, що він є опуклим.

7. Леся написала на дошці кілька попарно різних натуральних чисел. Андрійко не зміг вибрати серед цих чисел трьох, сума яких ділилася б на 3. Яку найбільшу кількість чисел могла виписати Леся?

Відповідь: 4 числа.

Розв’язання. Леся могла написати на дошці, приміром, такі чотири числа: 3, 4, 6, 7. Те, що сума жодних трьох із них не ділиться на 3, легко перевірити безпосереднім перебором.

 

                      

                                            8 клас

1. Теорема Безу
2. Метод невизначених коефіцієнтів.
3. Розкладання раціональних виразів на елементарні дроби.
4. Похідні пропорції.
5. Коло Ейлера.
6. Вписані і описані трикутники.
7. Співвідношення в колі.
8. Чотирикутник і коло.
9. Коло, як засіб розв’язування задач.
10. Задачі на нерівність трикутника.

 

 

                       

 

 

                                       Задачі

1.В рівності 2011 + 210 = 210 + 1197 пересунути дві цифри так, щоб вийшла правильна рівність.

Розв’язання. Легко перевірити справедливість рівності 2011 + 210 = 2¹º + 1197.        2221 = 1024 + 1197

2. Дано рівняння 20х + 11у = 2011. Знайти х+ у.

А: 20            Б: 31            В: 101           Г: 201           Д: 211

Розв’язання  х = 100, у = 1, тоді х+ у =100 + 1 = 101.

Відповідь. 101.

3. Знайти натуральні розв’язки рівняння а² b – 1 = 2011 ?

Розв’язання.Запишемо дане рівняння у вигляді а² b = 2012 = 2² • 503. Існує тільки один повний квадрат, що є дільником добутку 2² • 503. Отже, 2² • 503 – 1 = 2011.

Відповідь. а = 2, b = 503.

4.  Обчисліть значення виразу:

 .

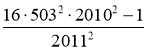
Відповідь: 4 044 119.

Розв’язання. Проведімо такі перетворення:

 

 

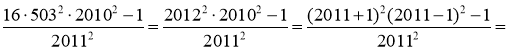
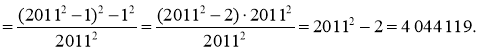
 5. Чи існують цілі числа x, y, z, які задовольняють рівність:

Відповідь: таких чисел не існує.

Розв’язання. Якби такі три числа x, y та z існували, принаймні два з них мали би однакову парність. Припустимо, це пара чисел x та y. Тоді сума х+у -парна, а отже парним мав би бути й добуток (х+у)(у+z)(z+х) . Число ж 2011, якому цей добуток повинен дорівнювати, — непарне. Одержана суперечність показує, що цілих чисел, які задовольняють умову, не існує.

6. У першій коробці кілька жовтих кульок, а у другій — кілька блакитних. Андрій перекладає декілька кульок із першої коробки в другу, після чого перемішує вміст другої коробки. Далі Леся перекладає таку ж саму кількість кульок із другої коробки в першу. Яких кульок тепер більше: жовтих у другій коробці чи блакитних у першій?

Відповідь: їх однакова кількість.

Розв’язання. Нехай діти перекладали з коробки в коробку по n кульок, причому серед n кульок, які переклала Леся, жовтих було m, а блакитних —  . Тоді жовтих кульок у другій коробці після Андрієвого перекладання було n, а після Лесиного стало n-m  . Блакитних же кульок у першій коробці після Андрієвого перекладання не було взагалі, а після Лесиного стало n-m  — стільки ж, скільки й жовтих кульок у другій коробці.

7. Знайдіть усі такі прості числа p та q, для яких число 2²+р²+q²   також є простим.

Відповідь:  p=2, q=3 або p=3, q=2.

Розв’язання. Якщо числа p та q непарні, то число 2²+р²+q²    парне і, очевидно, більше за 2, а тому не може бути простим. Отже, серед простих чисел p та q є парне, яке дорівнює 2. Припустимо, що таким є число p. Лишається знайти всі прості q, для яких простим є число q²+8.  .Помітимо, що коли число не ділиться на 3, себто дає при діленні на 3 остачу 1 або 2, квадрат цього числа дає від ділення на 3 остачу 1, а тому якщо q ділиться на 3 , то q²+8≡9 (mod 3) , тобто число q²+8˃3  ділиться на 3 і не є простим. Таким чином,qділиться на 3  , звідки q=3 . Аналогічно, якщо q=2 , то p=3  . Залишається підставити пари (2, 3) і (3, 2) у початковий вираз і пересвідчитися, що обидві справді дають просте число 17.

8. A й B — точки перетину кіл S₁ та S₂  таких, що центр кола S₁  лежить на колі S₂ , а центр кола S₂  лежить на колі S₁ . Точку C, відмінну від точки B, вибрано на колі S₁   так, що AC=AB . Знайдіть кути трикутника ABC.

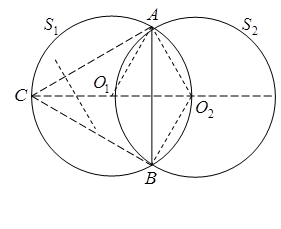
Відповідь: усі кути дорівнюють по 60⁰.

                                                 9 клас

1.Доведення нерівностей: а) спосіб підсилення; б) від супротивного; в) метод математичної індукції.

2.Нерівність Коші, Коші-Буняковського.

3.Врахування взаємного розташування коренів і параметра під час розв’язування нерівностей.

4.Площі фігур.

5. Теорема Птолемея.

6. Числа Фібоначі.

7. Способи знаходження сум.

 

                                Задачі

1. За яких значень параметра a рівняння

   має рівно два різних дійсних корені?

Відповідь:   

Розв’язання. Число x буде коренем рівняння тоді й лише тоді, коли  х=2  або ж х≥0   і    (а якщо так, то х=а² ). Тобто для того, щоб рівняння мало два різних корені, необхідно і достатньо, щоб існувало таке х≠2  , що . Це справджується для всіх 

2. Від’ємні числа a, b, c, d задовольняють такі умови:а=в+2с, а+с=в+d ,  b=d+c. Яке число більше: a чи c?

Відповідь:a<c 

Розв’язання. Виразимо b із кожного з трьох рівнянь:

 Тоді   , а також    . Оскільки всі числа від’ємні,  .

Зауважимо, що набір чисел, які задовольняють умову, існує: приміром,a=-6, b=-4,c=-1,d=-3.       

3. На дошці записано числа 1, 2, 3, ..., 101. Андрійко може вибрати серед записаних чисел довільні два a, b та записати замість них число  . Після 100-ї такої операції на дошці залишиться єдине число. Яке найбільше значення воно може мати?

Відповідь: 101.

Розв’язання. Оскільки всі числа на дошці залишатимуться невід’ємними на кожному кроці, а для невід’ємних чисел a та b завжди  , можемо стверджувати, що числа́, більшого за 101, на дошці опинитися на може. Число 101, з іншого боку, справді може залишитись останнім. Для цього Андрійку достатньо зробити так: спершу провести операції з парами чисел (1, 2), (3, 4), …, (99, 100) — записати замість кожної з цих пар одиницю. Далі він розіб’є отримані 50 одиниць на 25 пар і проведе операції з ними, внаслідок чого дістане 25 нулів, записаних на дошці разом із числом 101, яке Андрійко не чіпав. Далі хлопець по одному прибиратиме нулі, ставлячи їх у пари із числом 101.Отже, найбільшим числом, яке може лишитися після 100 операцій, є число 101.

4. Знайдіть усі натуральні значення n, для яких обидва числа 9n+28   та 5+n   є точними квадратами.

Відповідь: n=4

Розв’язання. Нехай деяке число n задовольняє умови задачі, причому  9n+28=x² та n+5=y² , де x та y — цілі і, без втрати загальності, додатні числа. Тоді маємо:(3y+x)(3y-x)=9y²-x²=9(n+5)-(9n+28)=45-28=17.Оскільки  3y+x˃1 , а 17 — просте число, повинна

справджуватися система:

 

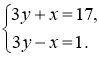
Звідси відразу знаходимо, що y=3  , а n=y²-5=4  . Перевіркою переконуємось, що значення n=4   задовольняє умову задачі.

5. У трикутнику ABC проведено бісектрису BD. Відомо, що центр описаного навколо   кола збігається із центром кола, що вписане у трикутник ВСD  . Знайдіть кути трикутника АВС .

Відповідь: ےА=72º, ےВ=72º,ےС=36º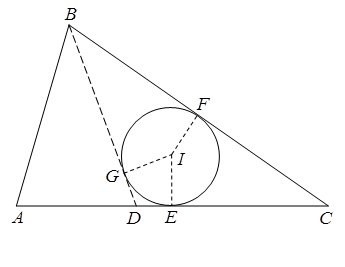  

Розв’язання. Позначмо спільний центр кіл через I, а точки дотику вписаного у ΔВСD  кола до сторін CD, BC і BD через E, F, G відповідно (рис. 5). Відрізки IE та IF — серединні перпендикуляри до сторін AC й BC відповідно, а тому AE=CE  та BF=CF . Із властивостей дотичних до кола BG=BF, CF=CE  і DG=DE , тому BD=BG+DG=BF+DG=CF+DE=CE+DE=CD. Також маємо, що DC=2CF=2CE=AC. Отже, трикутники BDC та ACB рівнобедрені. Звідси маємо, що ےBAC=ےABC=2ےDBC=2ےBCA180º=ےBAC+ےABC+ےBCA=5ےBCAےBCA=36º,ےBAC=ےABC=2ےBCA=72º

                                    10 клас

1.Теорема Вейєрштраса.

2. Рівняння що містять цілу і дробову частини та способи їх розв’язування.

3. Використання властивостей функції до розв’язування задач з параметрами.

4. Тригонометричні рівняння і нерівності з параметрами.

                       

                                    Задачі

Задача 1.

Містер Сміт, зайшовши в магазинчик, промовив : “Ей, продавець, скільки ти хочеш за сім?”- Двадцять центів, прошепотів зляканий торговець- А за тридцять сім?- Сорок центів.- Добре, заверни мені двісті сімдесят два.- З Вас шістдесят центів, містер. Запитання, що купив Містер Сміт?

Задача 2.  ОДТЧПШСВДД Що значать цей набір букв? Цю загадку учень 1-го класу вирішує за п’ять хвилин, старшокласник – за 15 хвилин, студент – за годину, професор – не вирішить ніколи. Що ховається за цими буквами?

Задача 3.  Із гнізда вилетіло 3-и ластівки? Яка ймовірність того, що через 15 секунд вони будуть в одній площині?

Задача 4. Начальник цеха запросив на нараду декілька чоловік. Кожний член наради, входячи в кабінет, потиснув руку кожному з присутніх. Скільки було членів наради, якщо було зафіксовано 78 рукостискань.

Задача 5

За яких значень параметра a рівняння :

має рівно три різних дійсних корені?

Відповідь:

Розв’язання. Рівняння можна переписати як , тому число x буде коренем цього рівняння тоді й лише тоді, коли , або — тобто і . Таким чином, рівняння матиме три різні корені тоді й тільки тоді, коли , причому і , тобто і

Задача 6

 Нескінченна спадна геометрична прогресія має перший член m, знаменник , а сума її членів дорівнює 3. Знайдіть усі можливі пари за умови, що m та n — натуральні числа.

Відповідь:

Розв’язання. Оскільки сума членів геометричної прогресії, описаної в умові задачі, дорівнює 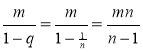, нам необхідно знайти всі натуральні m та n такі, що . Можемо записати:

Звідси, оскільки n — натуральне і не дорівнює 1, , а

Задача7

 У скільки способів можна розфарбувати всі 13 частин рис. 6 у три кольори так, щоб жодні дві частини, пофарбовані однаково, не мали спільної межі? Два розфарбування вважаються різними, якщо хоча б одна з 13 частин пофарбована по-різному.

    

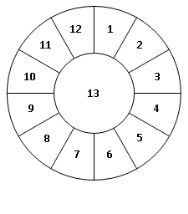
Розв’язання. Центральну частину можна пофарбувати в один із трьох кольорів. Тоді всі 12 секторів доведеться фарбувати в інші два кольори, адже кожен із секторів має спільну межу із центральною частиною. Сектор 1 можна пофарбувати у довільний із двох кольорів, а кольори решти секторів встановлюються після цього автоматично: сектор 2 має бути пофарбовано в колір, відмінний від кольору центральної частини і сектора 1; сектор 3 повинен бути пофарбований у колір, відмінний від кольору центральної частини й сектора 2 і т. д. Легко бачити, що таке розфарбування справді задовольнятиме умову задачі, адже пара секторів 12 і 1 також буде розфарбована по-різному.

Отже, маємо варіантів розфарбування.

Задача 8

 Доведіть, що для будь-яких дійсних чисел справджується нерівність:

Розв’язання. Щоб довести нерівність, можна розглянути випадки: всі можливі комбінації знаків виразів , та . Утім, можна зробити простіше — скористатися нерівністю , яка справджується для довільного дійсного числа a:

Задача 9 У чотирикутнику ABCD, що вписаний у коло, діагональ AC є бісектрисою кута DAB. На промені AD за точкою D вибрано точку E. Доведіть, що тоді й тільки тоді, коли

 

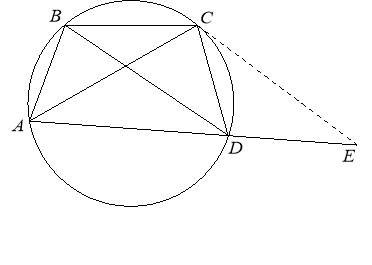Розв’язання. AC — бісектриса, тому, як відомо, (рис. 7). Крім того, .Якщо , то (за двома сторонами та кутом між ними), звідки .

Навпаки, якщо , то , звідки (за рівними кутами та парою сторін )

 

Задача 10.

 У три відра налито воду. Якщо чверть води з першого відра перелити до другого, а потім чверть води з другого перелити у третє, то в кожному відрі буде по 9 літрів води. Скільки літрів води було спочатку у третьому відрі.

Задача11. Потяг проходить міст довжиною 450 метрів за 45 секунд. А повз будки стрілочника – за 15 секунд. Знайти довжину потяга та його швидкість.

Задача 12.Чому дорівнює об’єм кристала?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

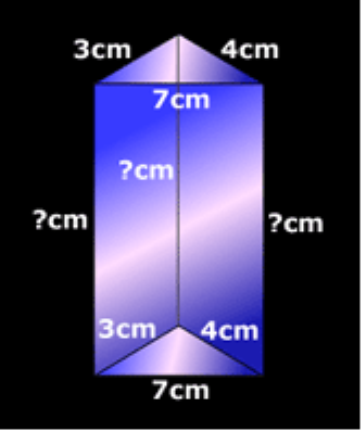
                                         11 клас

1.Асимптоти графіків. Перетворення графіків.

2.Функціональні рівняння Коші.

3.Використання похідної 1-го та 2-го порядків до доведення нерівностей.

4.Теорема Больцано-Коші.

5.Комбінаторика та Біном Ньютона.

6. Метод математичної індукції.

 

                              Задачі

1. Знайти всі розв’язки рівняння 2011^х – 2010^х = 1.

Розв’язання

Запишемо рівняння у вигляді .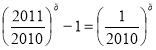

Функція в лівій частині рівняння зростає, а в правій частині спадає. Тому рівняння має не більше одного кореня.

Помічаємо, що х = 1 є коренем рівняння.

Відповідь. 1.

2. . Знайдіть усі значення , що задовольняють рівняння:

Відповідь:

Розв’язання. Зі співвідношення

дістаємо рівність , з якої, враховуючи, що , маємо, що

3. Позначимо через P(n) та S(n) відповідно добуток та суму цифр натурального числа n. Наприклад, , . Знайдіть усі двоцифрові числа n, для яких справджується рівність: .

Відповідь: 19, 29, 39, 49, 59, 69, 79, 89, 99.

Розв’язання. Нехай шукане двоцифрове число , . Рівняння з умови набуває такого вигляду:

Отже, умову задовольняють усі двоцифрові числа, що закінчуються на 9, і лише вони.

 

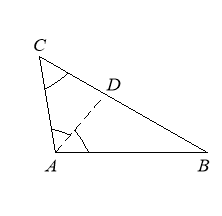4. У трикутнику ABC відрізок AD — бісектриса Виявилося, що , , а — рівнобедрений з вершиною D. Знайдіть довжини сторін

Відповідь:

Розв’язання. Зрозуміло, що (рис. 8). Із рівності кутів випливає, що , що дає співвідношення:

Звідси ,

Зауважимо, що трикутник зі сторонами справді задовольняє умову задачі: бісектриса AD ділить сторону BC у відношенні і дорівнює, після застосування теореми косинусів до трикутників ACB й ACD, 36.

5. У кожній клітинці квадратної таблиці міститься число 0 або число 1. Поряд із таблицею записали 10 чисел: суми значень у кожному з 4 рядків, суми значень у кожному з 4 стовпчиків і суми чисел на кожній із 2 великих діагоналей (тих діагоналей, що містять по чотири клітинки). Доведіть, що серед одержаних десяти чисел є принаймні три однакових.

Розв’язання. У кожному рядку, стовпчику та на кожній діагоналі містяться чотири числа, кожне з яких дорівнює 0 або 1, тому кожна записана сума може бути одним із п’яти чисел: 0, 1, 2, 3, 4. Якби серед 10 сум не було трьох однакових, це означало би, що кожне з п’яти можливих значень трапляється серед сум рівно двічі. Нехай це справді так. Розгляньмо одну з двох ліній, сума чисел на якій дорівнює 4; така лінія складається виключно з одиниць. Це не може бути діагональ, адже тоді в кожному рядку й у кожному стовпчику містилася би принаймні одна одиниця, тобто кількість ліній із сумою 0 була б меншою за дві. Хай тоді, без втрати загальності, лінія із сумою 4 — рядок. Це означає, що в кожному стовпчику й на кожній діагоналі є принаймні одна одиниця. Тоді дві лінії із сумою чисел 0 — теж рядки. Але в такому випадку друга лінія із сумою 4 теж не може бути ані стовпчиком, ані діагоналлю, тобто є рядком. Отже, маємо по два рядки із сумами 0 та 4, що означає, що сума чисел у кожному з чотирьох стовпчиків дорівнює 2, а це суперечить припущенню, що кожне значення від 0 до 4 трапляється серед сум рівно двічі. Одержана суперечність і завершує доведення.

 

6. Функція задовольняє такі умови:

• 
• 

Знайдіть значення

Відповідь:

Розв’язання. Для довільного , звідки . Використавши умову , матимемо:

Із допомогою методу математичної індукції покажемо, що . Базу індукції доведено вище. Індукційний перехід здійснимо, скориставшись співвідношенням :

Неважко індукцією показати й те, що функція справді задовольняє умову задачі: якщо , то

Отже,  

                                     

                                     Література

1. 2008 найкращих загадок / Упор. Г.Басюк. – Тернопіль: Яблуко. – 2008.– 320с.

2. Атамась В.В. Збірник задач з веселої математики / В.В Атамась. – Черкаси. – 1997.

3. Басанько А.М. За лаштунками підручника з математики. 5-7 клас / А.М. Басько, А.О. Романенко. – Тернопіль: Підручники і посібники. – 2005.

4. Буковська О. І. Математична логіка. 5-9класи / О.І Буковська. – X.: Основа. – 2005.

5. Волосюк М.А. Математичний тренажер ./ М.А. Волосюк. – Х.:ТОВ «Нова тема». – 2009. – 144с.

6. Друзь Б. Математична мозаїка. К.: Веселка, 1991. - 130 с.

7. Корнієнко Т.Л. Тиждень математики / Т.Л. Корнієнко, В.І. Фіготіна. – Х.: Ранок. – 2008.

8. Кривошея Т.М. Розкриймо дітям красу математичних міркувань / Т.М. Кривошея // Початкова школа. – 2000. – № 3. – С. 11-14.

9. Лишенко Г.П. Систематизація та методика розв'язування задач з логічним навантаженням. / Г.П. Лишенко // Початкова школа. – 1986. – №1. – С. 7-10.

10. Математичні розминки в 5 – 6  класах: Посібник. - Творча група «Гармонія» Решетилівської ЗОШ І-ІІ ступенів, 2006. –  23 с.

11. Математичні олімпіадні змагання школярів України: 2007-2008 та 2008-2009 / За ред. Б.В. Рубльова. – Львів: Каменяр. – 2010.

12. Позакласні заходи з математики. 5-8 класи / Упоряд. В. Морачова, І. Соколовська. – К. : Редакція загальнопедагогічних газет. – 2005. – 128с.

13. Позакласні заходи з математики. 9-11 класи: Збірник / Упоряд. І. Соколовська. – К.: Редакції загальнопедагогічних газет. – 2004. – 119с.

14. Підручна М.В. Математика. Позакласна робота / М.В. Підручна, Г.М. Янченко. – Тернопіль. – 1999.

15. Підручна М.В. Математика. Позакласна робота / М.В. Підручна, Г.М. Янченко. – Тернопіль. – 2001.

16. http://www.kangaroo.com.ua/index.php?r=pages/view&alias=archive

 

 

 

 

                                     Зміст

1.Анотація-----------------------------------------------------------------------        1

2.Вступ--------------------------------------------------------------------------          2

3.Логічні задачі, як шлях до творчого розвитку мислення учнів ----  3

4.Цікава математика у розв’язках і міркуваннях-------------------------  6

5.Використання історичного матеріалу на уроках математики,

як засіб розвитку пізнавальної активності учнів-------------------------   7

6. Перелік основних тем та підбірка задач з розвязками:

• 5 клас  -----------------------------------------------------------------------   10
• 6 клас  -----------------------------------------------------------------------   16
• 7 клас  -----------------------------------------------------------------------   19
• 8 клас  -----------------------------------------------------------------------    23
• 9 клас  -----------------------------------------------------------------------    27
• 10 клас ----------------------------------------------------------------------    30
• 11 клас ----------------------------------------------------------------------    35
• 7. Література --------------------------------------------------------------    38