Контрольні роботи з алгебри і геометрії 7 клас
Контрольні роботи
з алгебри і геометрії
7 клас
Упорядник:
Рак Любов Миколаївна, вчитель математики Лукімської ЗОШ І-ІІІ ступенів Оржицької районної ради Полтавської області, учитель вищої кваліфікаційної категорії, стаж роботи 29 років
Зміст
Вступ………………………………………………………….……...…………….4
Діагностична контрольна робота з алгебри…………………...………………...5
Контрольна робота № 1 з теми «Лінійне рівняння з однією змінною»…….....7
Контрольна робота №2 зтеми «Степінь з натуральним показником.
Одночлени»………………………………………………………………………..9 Контрольна робота № 3 з теми «Многочлени. Дії над многочленами»……...11
Контрольна робота № 4 з теми «Формули скороченого множення. Розкладання многочленів на множники»………………………………………13
Контрольна робота № 5 з теми «Розкладання многочленів на множники різними способами»……………………………………………………………..15
Контрольна робота № 6 з теми «Функції»……………………………………..17
Контрольна робота № 7 з теми «Системи лінійних рівнянь з двома змінними»………………………………………………………………………...19Контрольна робота №8 «Повторення і систематизація навчального матеріалу»………………………………………………………………………..21
Контрольна робота № 1 з теми «Найпростіші геометричні фігури»…………23
Контрольна робота № 2 з теми «Ознаки рівності трикутників. Рівнобедрений трикутник»……………………………………………………………………….25
Контрольна робота № 3 з теми «Паралельні прямі. Сума кутів трикутника».27
Контрольна робота № 4 з теми «Коло та круг»………………………………..29
Контрольна робота № 5 з теми «Повторення і систематизація навчального матеріалу»………………………………………………………………………..31
Відповіді……………………………………………………………….................33
Список використаних джерел…………………………………………………..38
Вступ
Посібник містить тематичні контрольні роботи з алгебри та геометрії у 7 класі, які складені у відповідності з програмою для загальноосвітніх навчальних закладів та обов’язковими результатами навчання.
Посібник містить діагностичну контрольну роботу, 8 тематичних контрольних робіт та підсумкову контрольну роботу з алгебри; 4 тематичних контрольних робіт та підсумкову контрольну роботу з геометрії. Кожна контрольна робота складається з двох рівнозначних варіантів.
Завдання 1 – 6 початкового та середнього рівнів є тестовими (з вибором однієї правильної відповіді) або відкритої форми з короткою відповіддю. Правильне розв’язання завдань початкового та середнього рівнів оцінюються 6 балами (кожне – по 1 балу).
Завдання 7 – 8 є завданнями достатнього рівня, їх правильне розв’язання оцінюється 3 балами (кожне по 1,5 бала) і передбачає наведення короткого запису розв’язання з поясненням основних моментів та правильну відповідь.
Завдання 9 - завдання високого рівня – його правильне розв’язання оцінюється 3 балами. Таке завдання вважається виконаним правильно,
якщо учень навів розгорнутий запис розв’язування з обґрунтуванням
кожного його етапу та дав правильну відповідь.
Діагностична контрольна робота
Варіант 1
Початковий і середній рівень (6 балів)
1.Знайдіть найбільший спільний дільник чисел: 60 і 45
А)5 Б)30 В)15 Г)90
2.Знайдіть невідомий член пропорції: 
А)9 Б)15 В)20 Г)30
3.Вкажіть правильну нерівність:
А)-6,64>-6,71 Б)-0,23˂-0,34
В)-0,01>-0,002 Г)5,1˂-6,9
4.Обчисліть значення виразу:
(4,8-6,6):6
А)0,3 Б)-3 В)3 Г)-0,3
5.Виконайте дії: 
А)
Б)
В)
Г)
6.Учень купив 56 зошитів, 
з них становили зошити в клітинку. Скільки зошитів у клітинку купив учень?
А)20 Б)32 В)35 Г)40
Достатній рівень (3 бали)
7.Спростіть вираз -4(6-2а)-2(а-8) і знайдіть його значення, якщо а=0,1.
8.Позначте на координатній площині точки А(6;1) і С(-2;-3), проведіть відрізок АС. Знайдіть координати точки перетину відрізка з віссю абсцис.
Високий рівень (3 бали)
9.На першому складі було у 3 рази більше шаф, ніж на другому. Коли з першого складу вивезли 20 шаф, а на другий привезли 16 шаф, то на обох складах шаф стало порівну. Скільки шаф було на кожному складі спочатку?
Діагностична контрольна робота
Варіант 2
Початковий і середній рівень (6 балів)
1.Знайдіть найменше спільне кратне чисел: 30 і 45
А)5 Б)30 В)15 Г)90
2.Знайдіть невідомий член пропорції: 6:15=8:х
А)9 Б)15 В)20 Г)30
3.Вкажіть правильну нерівність:
А)-3,1˂-4,3 Б)-6,14˂-6,25
В)-0,08>-0,4 Г)-5,1>5,06
4.Обчисліть значення виразу:
(-0,8-1,3):7
А)0,3 Б)-3 В)3 Г)-0,3
5.Виконайте дії: 
А) Б) В) Г)
6.Мама спекла пиріжки. Пиріжків із вишнями було 25, що становило 
від усіх пиріжків. Скільки пиріжків із вишнями спекла мама?
А)20 Б)32 В)35 Г)40
Достатній рівень (3 бали)
7.Спростіть вираз -6(2у-5)-2(3-7у) і знайдіть його значення, якщо у=-0,1.
8.Позначте на координатній площині точки А(2;-3) і С(-4;3), проведіть відрізок АС. Знайдіть координати точки перетину відрізка з віссю абсцис.
Високий рівень (3 бали)
9.В одному ящику було в 5 разів більше апельсинів, ніж у другому. Після того, як з першого ящика взяли 25 апельсинів, а з другого 1 апельсин, то апельсинів у ящиках стало порівну. Скільки апельсинів було в кожному ящику спочатку?
Контрольна робота №1 з теми «Лінійне рівняння з однією змінною»
Варіант 1
Початковий і середній рівень (6 балів)
1.Серед даних рівнянь вибрати рівняння з однією змінною:
А)3х²+1=10 Б)7х-у=27 В)-4х-18=1 Г)
2.Знайдіть корінь рівняння:
-2х-5=9.
А)7 Б)-9 В)2 Г)-7
3.Вкажіть рівняння, яке рівносильне рівнянню: 4х-7=1
А)-2х+11=9 Б)7х-9=5 В)0,3х=6 Г)3х+2=-1
4.Розв’яжіть рівняння: 9х-8=7х+5.
А)5,5 Б)6,5 В)9,5 Г)7
5.Знайдіть значення змінної, для якого рівні вирази: 9,9+х і 3,6-2х.
А)-0,5 Б)-2,1 В)-3,5 Г)4
6.Одне число на 8 менше за друге, а сума чисел 26. Знайдіть ці числа.
Достатній рівень (3 бали)
7. Розв’яжіть рівняння:
2+3(х+1)=3+5(х-2).
8.Знайдіть корінь рівняння:
.
Високий рівень (3 бали)
9.Від станції до турбази туристи йшли зі швидкістю 4 км/год, а назад зі швидкістю 5 км/год, тому на той самий шлях затратили на 1 год менше. Знайдіть відстань від станції до турбази.
Контрольна робота №1 з теми «Лінійне рівняння з однією змінною»
Варіант 2
Початковий і середній рівень (6 балів)
1.Серед даних рівнянь вибрати рівняння з однією змінною:
А)-8х²+1=16 Б)-7х+2=44 В)-4х+3у=12 Г)
2.Знайдіть корінь рівняння:
-4х-12=24.
А)7 Б)-9 В)2 Г)-7
3.Вкажіть рівняння, яке рівносильне рівнянню: -5х+8=13.
А)-2х+11=9 Б)7х-9=5 В)0,3х=6 Г)3х+2=-1
4.Розв’яжіть рівняння: 9х-8=7х+5.
А)5,5 Б)6,5 В)9,5 Г)7
5.Знайдіть значення змінної, для якого рівні вирази: 4,2-2х і 3х+6.
А)-0,5 Б)-2,1 В)-3,5 Г)4
6. У одному ящику у 3 рази яблук більше, ніж у другому. Скільки кілограмів яблук у кожному ящику, якщо разом їх 32 кг?
Достатній рівень (3 бали)
7. Розв’яжіть рівняння:
5+2(х+1)=3-5(х+2).
8.Знайдіть корінь рівняння:
.
Високий рівень (3 бали)
9.Автомобіль проїжджає відстань між містами за 4 год. Якби він їхав зі швидкістю на 10 км/год більшою, то в дорозі був би на півгодини менше. Знайдіть відстань між цими містами.
Контрольна робота №2 з теми «Степінь з натуральним показником. Одночлени»
Варіант 1
Початковий і середній рівень (6 балів)
1.Записати у вигляді степеня з основою х:
а)(х
)², б) х
·х², в)х
: х².
А)х
Б)х³ В)х
Г)х
2.Піднесіть до куба одночлен: -2х²у³.
А)-9х
у
Б)-8х
у
В) 8х
у
Г) 9ху
3.Знайдіть значення виразу: а)(80-3
)
; б)7,3-5·2³.
А)1 Б)-1 В)-32,7 Г)-85,8
4.Спростіть вираз: а)(х³·х
)³; б)( 
)
.
А)х
Б)х
В)
Г)
5.Подайте в стандартному вигляді одночлен: -3х²у·2ху².
А)-6х²у² Б)-6х³у³ В)-9х³у
Г)-9х³у³
6. Розв’яжіть рівняння: а)х
+1=0; б)3х³·х+6=0.
Достатній рівень (3 бали)
7.Спростіть вираз:
(-
х³у)²·(-3ху³)³.
8. Знайдіть значення виразу:
а)
; б)(5
)
·
.
Високий рівень (3 бали)
9.Доведіть, що значення виразу 106
+44 кратне 10.
Контрольна робота №2 з теми «Степінь з натуральним показником. Одночлени»
Варіант 2
Початковий і середній рівень (6 балів)
1.Записати у вигляді степеня з основою х:
а)(х
)²; б) х
·х²; в)х
: х².
А)х
Б)х³ В)х
Г)х
2.Піднесіть до куба одночлен: -3х³у².
А)-9ху Б)-8ху В) 8ху Г) 9ху
3.Знайдіть значення виразу: а)(15-2); б)14,2-5²·2².
А)1 Б)-1 В)-32,7 Г)-85,8
4.Спростіть вираз: а)(х³·х
)³ ; б)( 
).
А)х Б)х В) Г)
5.Подайте в стандартному вигляді одночлен: 3х²у·(-3ху³).
А)-6х²у² Б)-6х³у³ В)-9х³у Г)-9х³у³
6. Розв’яжіть рівняння: а)х-1=0; б)3х³·х
+12=0.
Достатній рівень (3 бали)
7.Спростіть вираз:
(-
ху²)²·(-5х²у)³
8. Знайдіть значення виразу:
а)
, б)(2
)
·
.
Високий рівень (3 бали)
9.Доведіть, що значення виразу 105
-55 кратне 10.
Контрольна робота №3 з теми «Многочлени. Дії над многочленами»
Варіант 1
Початковий і середній рівень (6 балів)
1.Подайте многочлен у стандартному вигляді:
2х+3х²+х³-4х²-2х.
А)х²-х³ Б)х²+х³ В)х³-х² Г)х³-4х
2.Знайдіть значення многочлена х³-5х+6, якщо х=-2.
А)8 Б)-16 В)20 Г)0
3.Подайте у вигляді многочлена вираз:
-3х(2х-1)+4(х-3).
А)12х²-2х-6 Б)-6х²+7х-12 В)6х²-7х+12 Г)-12х²+2х+6
4.Знайдіть суму і різницю многочленів: -3х+2х² і 8х-х².
А)5х²+3х Б)х²+13х В)3х²-5х Г)х²+5х
5. Розв’яжіть рівняння: х²+3=(х-1)(х+3).
А)2 Б)3 В)5 Г)12
6.Спростіть вираз: (х+2)(х+12)-х(5-х)-2х²
і знайдіть його значення, якщо х=-3
А)5 Б)-3 В)-12 Г)9
Достатній рівень (3 бали)
7. Розв’яжіть рівняння: 
8. Подайте у вигляді многочлена вираз:
(а-1)(а+1)(а²+1)-1+а
.
Високий рівень (3 бали)
9.Доведіть, що для будь-якого натурального п значення виразу
п(п+5)-(п-3)(п+2) кратне числу 6.
Контрольна робота №3 з теми «Многочлени. Дії над многочленами»
Варіант 2
Початковий і середній рівень (6 балів)
1.Подайте многочлен у стандартному вигляді:
3х-5х²+х³+4х²-3х.
А)х²-х³ Б)х²+х³ В)х³-х² Г)х³-4х
2.Знайдіть значення многочлена 2х³-3х-6, якщо х=-2.
А)8 Б)-16 В)20 Г)0
3.Подайте у вигляді многочлена вираз:
-4х(2-3х)+6(х-1).
А)12х²-2х-6 Б)-6х²+7х-12 В)6х²-7х+12 Г)-12х²+2х+6
4.Знайдіть суму і різницю многочленів: 3х²+8х і 5х-2х².
А)5х²+3х Б)х²+13х В)3х²-5х Г)х²+5х
5. Розв’яжіть рівняння: х(х+3)=х²-5х+4.
А)2 Б)3 В)5 Г)12
6.Спростіть вираз: (х+3)(х-3)-(4-х)х-3х
і знайдіть його значення, якщо х=-3
А)5 Б)-3 В)-12 Г)9
Достатній рівень (3 бали)
7. Розв’яжіть рівняння: 
8. Подайте у вигляді многочлена вираз:
с
-(с-1)(с+1)+1.
Високий рівень (3 бали)
9.Доведіть, що для будь-якого натурального п значення виразу
(п-1)(п+1)-(п-7)(п-5) кратне числу 12.
Контрольна робота №4 з теми «Формули скороченого множення. Розкладання многочленів на множники»
Варіант 1
Початковий і середній рівень (6 балів)
1.Винесіть спільний множник за дужки: 3х²у
+9ху³.
А)3ху(х+у) Б)3ху³(ху+3) В)3х³у(ху+3) Г)3х²у(х+3у)
2.Розкладіть многочлен на множники: а(х-у)-х(х-у).
А)(х-у)(-х-а) Б)(х-у)(х+а) В)(х-у)(х-а) Г)(х-у)(а-х)
3.Подайте вираз у вигляді многочлена: а)(2а-3в)²; б)(7х+10)(7х-10).
А)36а²-4 Б)4а²-12ав+9в² В)49х²-100 Г)9х²+12ху+4у²
4.Розкладіть многочлен на множники: а)в²-81; б)с²+8с+16.
А)(в-8)(в+8) Б)(в-9)(в+9) В)(с+4)(с+4) Г)(с+5)(с+5)
5. Розв’яжіть рівняння: 8х²-24х=0.
А)0; -3 Б)0; 2 В)0; 3 Г)0; -2
6.Розкладіть на множники способом групування: 9ху-ув+9хв-в².
Достатній рівень (3 бали)
7.Спростіть вираз (х-2)(х+2)- (х+5)² і обчисліть його значення, якщо х=-1.
8. Розв’яжіть рівняння: а)3(х-3)-х(3-х)=0; б)х³-5х²+2х-10=0.
Високий рівень (3 бали)
9.Доведіть, що вираз х²-14х+51 набуває додатніх значень при всіх значеннях х.
Контрольна робота №4 з теми «Формули скороченого множення. Розкладання многочленів на множники»
Варіант 2
Початковий і середній рівень (6 балів)
1.Винесіть спільний множник за дужки: 3ху²+9х³у.
А)3ху(х+у) Б)3ху³(ху+3) В)3х³у(ху+3) Г)3х²у(х+3у)
2.Розкладіть многочлен на множники: х(х-у)-а(х-у).
А)(х-у)(-х-а) Б)(х-у)(х+а) В)(х-у)(х-а) Г)(х-у)(а-х)
3.Подайте вираз у вигляді многочлена: а)(3х+2у)²; б)(6а-2)(6а+2).
А)36а²-4 Б)4а²-12ав+9в² В)49х²-100 Г)9х²+12ху+4у²
4.Розкладіть многочлен на множники: а)в²-64; б)с²-10с+25.
А)(в-8)(в+8) Б)(в-9)(в+9) В)(с+4)(с+4) Г)(с+5)(с+5)
5. Розв’яжіть рівняння: 8х²+24х=0.
А)0; -3 Б)0; 2 В)0; 3 Г)0; -2
6.Розкладіть на множники способом групування: 7х²+ху-7ху-у².
Достатній рівень (3 бали)
7.Спростіть вираз (х-3)(х+3)- (х-2)² і обчисліть його значення, якщо х=-1.
8. Розв’яжіть рівняння: а)5(2-х)-х(х-2)=0; б)3у³+9у²-у-3=0.
Високий рівень (3 бали)
9.Доведіть, що вираз х²-16х+71 набуває додатніх значень при всіх значеннях х.
Контрольна робота №5 з теми «Розкладання многочленів на множники різними способами»
Варіант 1
Початковий і середній рівень (6 балів)
1. Розкладіть многочлен на множники: 3х³-12х.
А)3х(х-4)(х+4) Б)3х(х-2)(х+2) В)4х(х-9)(х+9) Г)4х(х-3)(х+3)
2.Подайте у вигляді добутку двочлен: 125-х³.
А)(25-х)(25+х) Б)(х-3)(х+3) В)(5-х)(25+5х+5х²) Г)(х-3)(х²+3х+9)
3.Подайте у вигляді многочлена: (3х+1)(9х²-3х+1).
А)8х³+27 Б)9х²-6х+3 В)27х³+1 Г)4х²-12х+18
4. Розв’яжіть рівняння: у²-6у+9=0.
А)3 Б)7 В)-3 Г)-7
5.Запишіть у вигляді добутку вираз: а)4а²-9; б)4а²-12а+9.
А)(3х-1)(3х+1) Б)(2а-3)(2а-3) В)(3х-1)(3х-1) Г)(2а-3)(2а+3)
6.Розкладіть многочлен на множники : 3х²-6ху-2х+2у.
Достатній рівень (3 бали)
7.Установіть відповідність між рівняннями а)-г) і множинами їх коренів А-Г:
а)х²+4х+4=0 б)х²-4=0 в)х²-2х+1=0 г)х²+2х=0 .
А)1 Б)0; -2 В)-2 Г)2; -2
8.Подайте у вигляді квадрата двочлена: (10х+3т)²-(8х-4т)(8х+4т).
Високий рівень (3 бали)
9.Подайте у вигляді добутку вираз: а)(х-5)²-9; б)х²+2ху+у²-4;
в)
.
Контрольна робота №5 з теми «Розкладання многочленів на множники різними способами»
Варіант 2
Початковий і середній рівень (6 балів)
1. Розкладіть многочлен на множники: 4х³-36х.
А)3х(х-4)(х+4) Б)3х(х-2)(х+2) В)4х(х-9)(х+9) Г)4х(х-3)(х+3)
2.Подайте у вигляді добутку двочлен: х³-27.
А)(25-х)(25+х) Б)(х-3)(х+3) В)(5-х)(25+5х+5х²) Г)(х-3)(х²+3х+9)
3.Подайте у вигляді многочлена: (2х+3)(4х²-6х+9).
А)8х³+27 Б)9х²-6х+3 В)27х³+1 Г)4х²-12х+18
4. Розв’яжіть рівняння: у²+14у+49=0.
А)3 Б)7 В)-3 Г)-7
5.Запишіть у вигляді добутку вираз: а)9х²-1; б)9х²-6х+1.
А)(3х-1)(3х+1) Б)(2а-3)(2а-3) В)(3х-1)(3х-1) Г)(2а-3)(2а+3)
6.Розкладіть многочлен на множники : 4ху-8у²-3+6у.
Достатній рівень (3 бали)
7.Установіть відповідність між рівняннями а)-г) і множинами їх коренів А-Г:
а)х²+6х+9=0 б)х²-9=0 в)х²-4х+4=0 г)х²-2х=0 .
А)2 Б)0; 2 В)-3 Г)3; -3
8.Подайте у вигляді квадрата двочлена: (4х+3у)²-8у(4х+у).
Високий рівень (3 бали)
9.Подайте у вигляді добутку вираз: а)(х-6)²-64; б)х²-2ху+у²-9;
в)
Контрольна робота №6 з теми «Функції»
Варіант 1
Початковий і середній рівень (6 балів)
1. Знайдіть значення функції, якщо значення аргументу дорівнює 2, а функція задана формулою: у=-2х+7.
А)2,5 Б)3 В)5,6 Г)-13
2.Знайдіть значення аргументу для функції у=-2х+7, якщо значення функції дорівнює -3.
А)4 Б)5 В)-5 Г)3
3.Через яку з даних точок проходить графік функції у=8х-3?
А)(-1; 5) Б)(3; 1) В)(0; 5) Г)(1; 5)
4.Знайдіть область визначення функції: а)у=
; б)у=
.
А)всі числа крім 3 Б)всі числа В)всі числа крім -3 Г)всі числа крім -5
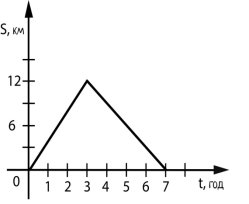
5.На рисунку зображено графік руху
туриста. З якою швидкістю турист
ішов перші 3 години?
А)3км/год Б)4км/год В)5км/год Г)6км/год
6.Побудуйте графік функції у=3х-2.
Достатній рівень (3 бали)
7.Не виконуючи пбудови, знайдіть координати точок перетину графіка функції у=7х-35 з осями координат.
8.Приякому значенні k графік функції у=kх-6 проходить через точку
А(-2; 20)?
Високий рівень (3 бали)
9.Побудуйте графік функції у =
Контрольна робота №6 з теми «Функції»
Варіант 2
Початковий і середній рівень (6 балів)
1. Знайдіть значення функції, якщо значення аргументу дорівнює 2, а функція задана формулою: у=-8х+3.
А)2,5 Б)3 В)5,6 Г)-13
2.Знайдіть значення аргументу для функції у=-8х+3, якщо значення функції дорівнює -21.
А)4 Б)5 В)-5 Г)3
3.Через яку з даних точок проходить графік функції у=-2х+7?
А)(-1; 5) Б)(3; 1) В)(0; 5) Г)(1; 5)
4.Знайдіть область визначення функції: а)у=
; б)у=
.
А)всі числа крім 3 Б)всі числа В)всі числа крім -3 Г)всі числа крім -5
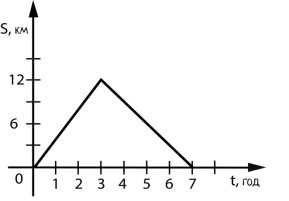5.На рисунку зображено графік руху
туриста. З якою швидкістю турист
ішов останні 4 години?
А)3км/год Б)4км/год В)5км/год Г)6км/год
6.Побудуйте графік функції у=-3х+2.
Достатній рівень (3 бали)
7.Не виконуючи пбудови, знайдіть координати точок перетину графіка функції у=42-7х з осями координат.
8.Приякому значенні k графік функції у=kх-6 проходить через точку
В(3; -21)?
Високий рівень (3 бали)
9.Побудуйте графік функції у =
Контрольна робота №7 з теми «Системи лінійних рівнянь з двома змінними»
Варіант 1
Початковий і середній рівень (6 балів)
1.З даного рівняння виразіть змінну х через змінну у: 8у+2х=12.
А)х=12-8у Б)у=10-2х В)у=30-6х Г)х=6-4у
2. Скільки розв’язків має система рівнянь: 
?
А)один Б)жодного В)безліч Г)визначити неможливо
3.Вкажіть розв’язок системи рівнянь: 
А)(1; 1) Б)(1; 3) В)(2; 4) Г)(0; 2)
4.Розв’яжіть систему рівнянь способом додавання : 
А)(1; 1) Б)(-1; 1) В)(2; 1) Г)(-2; 1)
5. Розв’яжіть систему рівнянь способом підстановки: 
А)(1; 1) Б)(2; 2) В)(2; -2) Г)(-2; 2)
6.Серед наведених систем вказати ту, що відповідає умові задачі.
Сума чисел 20, 10% першого числа більші за 15% другого на 5. Які це числа?
А)
Б)
В)
Г)
Достатній рівень (3 бали)
7. Розв’яжіть систему рівнянь: 
8. Розв’яжіть систему рівнянь графічним способом: 
Високий рівень (3 бали)
9. Розв’яжіть задачу з допомогою системи рівнянь.
Скільки грамів 2-відсоткового і 5-відсоткового розчинів солі потрібно взяти, щоб отримати 270 г 3-відсоткового розчину?
Контрольна робота №7 з теми «Системи лінійних рівнянь з двома змінними»
Варіант 2
Початковий і середній рівень (6 балів)
1.З даного рівняння виразіть змінну у через змінну х: 3у+6х=30.
А)х=12-8у Б)у=10-2х В)у=30-6х Г)х=6-4у
2. Скільки розв’язків має система рівнянь: 
?
А)один Б)жодного В)безліч Г)визначити неможливо
3.Вкажіть розв’язок системи рівнянь: 
А)(1; 1) Б)(1; 3) В)(2; 4) Г)(0; 2)
4.Розв’яжіть систему рівнянь способом додавання : 
А)(1; 1) Б)(-1; 1) В)2; 1) Г)(-2; 1)
5. Розв’яжіть систему рівнянь способом підстановки: 
А)(1; 1) Б)(2; 2) В)(2; -2) Г)(-2; 2)
6.Серед наведених систем вказати ту, що відповідає умові задачі.
Одне число більше за друге на 20, 10% першого числа та 15% другого числа становлять 5. Які це числа?
А) Б) В) Г)
Достатній рівень (3 бали)
7. Розв’яжіть систему рівнянь: 
8. Розв’яжіть систему рівнянь графічним способом: 
Високий рівень (3 бали)
9. Розв’яжіть задачу з допомогою системи рівнянь.
Підручник і альбом коштували разом 70 грн. Після того,як підручник подешевшав на 20%, а альбом подорожчав на 20%, вони стали коштувати разом 68 грн. Знайдіть початкову ціну кожного з них.
Контрольна робота №8 з теми «Повторення і систематизація навчального матеріалу»
Варіант 1
Початковий і середній рівень (6 балів)
1. Обчисліть значення виразу: 
.
А) 36 Б)1 В)49 Г)6
2.Виконати множення одночленів: 0,5х³у²·8ху
.
А)4х³у
Б)-2х³у
В)4х
Г)2х²у
3.Перетворіть у многочлен вираз: (6а+4с)².
А)36а²+16с² Б) 36а²+48ас+16с² В)25с²-4а² Г) 25с²-20ас+4а²
4.Через яку з даних точок проходить графік рівняння х-2у=7?
А)(-2; 7) Б)11; 2) В)(5; 1) Г)(2; -2)
5.Розкладіть многочлен на множники: а)49с²-4; б)4х²у²-4у².
А)4ху(х-у)(х+у) Б)4у²(х-1)(х+1) В)(7с-2)(7с+2) Г)(7-2с)(7+2с)
6.Знайдіть корінь рівняння: (х+10)(х-6)-(х+1)(х-1)=1.
Достатній рівень (3 бали)
7. Розв’яжіть систему рівнянь: 
8.Побудуйте графік функції у=4-2х. За допомогою графіка установіть, при яких значеннях аргументу функція набуває додатніх значень.
Високий рівень (3 бали)
9.Теплохід проходить за 2 год за течією річки і 3 год проти течії 85 км. Відомо, що за 3 год за течією річки він проходить на 30 км більше, ніж за
2 год проти течії. Знайдіть швидкість руху теплохода за течією річки і швидкість його руху проти течії.
Контрольна робота №8 з теми «Повторення і систематизація навчального матеріалу»
Варіант 2
Початковий і середній рівень (6 балів)
1. Обчисліть значення виразу: 
.
А) 36 Б)1 В)49 Г)6
2.Виконати множення одночленів: -5ху
·0,4х²у
.
А)4х³у Б)-2х³у В)4х Г)2х²у
3.Перетворіть у многочлен вираз: (5с-2а)².
А)36а²+16с² Б) 36а²+48ас+16с² В)25с²-4а² Г) 25с²-20ас+4а²
4.Через яку з даних точок проходить графік рівняння 3х+у=1?
А)(-2; 7) Б)11; 2) В)(5; 1) Г)(2; -2)
5.Розкладіть многочлен на множники: а)49-4с²; б)4х³у-4ху³.
А)4ху(х-у)(х+у) Б)4у²(х-1)(х+1) В)(7с-2)(7с+2) Г)(7-2с)(7+2с)
6.Знайдіть корінь рівняння: (х-5)(х+8)-(х-7)(х+7)=0.
Достатній рівень (3 бали)
7. Розв’яжіть систему рівнянь: 
8.Побудуйте графік функції у=-2х-4. За допомогою графіка установіть, при яких значеннях аргументу функція набуває додатніх значень.
Високий рівень (3 бали)
9.Двоє робітників виготовили 123 деталі. Перший робітник працював 7 год, а другий – 10 год. Скільки деталей виготовляв за 1 год кожний робітник, якщо перший за 4 год зробив на 6 деталей більше, ніж другий за 5 год?
Контрольна робота №1 з теми «Найпростіші геометричні фігури»
Варіант 1
Початковий і середній рівень (6 балів)
1.Точка В лежить між точками А і С, АС=45см, ВС=23см. Знайдіть відрізка АВ.
А)22см Б)23см В)45см Г)20см
2.Промінь ОК лежить між сторонами кута СОD, 
СОD=120°, 
DОК=55°. Знайдіть 
СОК.
А)10° Б)55° В)65° Г)90°
3.Один з суміжних кутів 48°. Яка міра другого кута?
А)53° Б)127° В)132° Г)48°
4.Промінь ОР – бісектриса кута АОВ. Знайдіть кут АОВ, якщо 
РОА=40°30´.
А)140° Б)150°30´ В)81° Г)139°30´
5.Градусні міри суміжних кутів пропорційні числам 4 і 5. Знайдіть більший кут.
А) 40° Б)80° В)100° Г)140°
6. Один з кутів, що утворилися при перетині двох прямих , дорівнює 36°. Знайдіть решту кутів.
Достатній рівень (3 бали)
7.Промінь ОМ лежить між сторонами кута АОВ, 
АОВ=100°. Знайдіть кути АОМ і ВОМ, якщо 
°.
8.Точки А, В, С лежать на одній прямій. Відомо, що АВ=8см, ВС=16см. Знайдіть АС.
Високий рівень (3 бали)
9. Дано:АОВ=100°, АОС=37°.
Знайти: ВОС. Розгляньте можливі випадки.
Контрольна робота №1 з теми «Найпростіші геометричні фігури»
Варіант 2
Початковий і середній рівень (6 балів)
1.Точка В лежить між точками А і С, АС=45см, ВС=12см. Знайдіть довжину відрізка АВ.
А)22см Б)23см В)45см Г)32см
2.Промінь ОК лежить між сторонами кута СОD, СОD=120°, СОК=65°. Знайдіть DОК.
А)10° Б)55° В)65° Г)90°
3.Один з суміжних кутів 53°. Яка міра другого кута?
А)53° Б)127° В)132° Г)48°
4.Промінь ОР – бісектриса кута АОВ. Знайдіть кут АОВ, якщо РОА=29°30´.
А)59° Б)150°30´ В)81° Г)139°30´
5.Градусні міри суміжних кутів пропорційні числам 8 і 10. Знайдіть менший кут.
А) 40° Б)80° В)100° Г)140°
6. Один з кутів, що утворилися при перетині двох прямих , дорівнює 72°. Знайдіть решту кутів.
Достатній рівень (3 бали)
7.Промінь ОМ лежить між сторонами кута АОВ, АОВ=100°. Знайдіть кути АОМ і ВОМ, якщо 
°.
8.Точки А, В, С лежать на одній прямій. Відомо, що АВ=7см, ВС=15см. Знайдіть АС.
Високий рівень (3 бали)
9. Дано:АОВ=123°, АОС=27°.
Знайти: ВОС. Розгляньте можливі випадки.
Контрольна робота №2 з теми «Ознаки рівності трикутників. Рівнобедрений трикутник»
Варіант 1
Початковий і середній рівень (6 балів)
1.Укажіть пару рівних сторін трикутників, якщо ∆МНК=∆РВС
А)МН=РВ Б)МН=СР В)НК=СР Г)НК=РВ
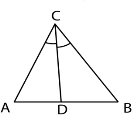
2.Визначте, яка з наведених рівностей випливає
з умови того, що у різносторонньому
трикутнику АВС відрізок СD є бісектрисою.
А)
САD=
СВD Б)АD=ВD В)АС=ВС Г)
АСD=
DСВ
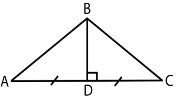
3.Визначте,за якими елементами
два трикутники,
зображені на рисунку, рівні.
А)за двома сторонами і кутом між ними Б) за трьома сторонами
В)за стороною і прилеглими кутами Г)неможливо визначити
4.У трикутнику АВС АВ=6см, ВС=7см. Знайдіть периметр трикутника, якщо його бічною стороною є АВ.
А) 13см Б)15см В)19см Г)20см
5.У рівнобедреному трикутнику АВС ВС – основа, АD – медіана. Знайдіть кут ВАС, якщо 
ВАС-
ВАD=30°.
А)30° Б)50° В)60° Г)90°
6.У трикутнику АВС АВ=АС, периметр трикутника дорівнює 125 см. Знайдіть ВС, якщо АВ=40 см.
Достатній рівень (3 бали)
7.Знайдіть сторони рівнобедреного трикутника, якщо його периметр дорівнює 100 см, а основа відноситься до бічної сторони, як 4:3.
8.Відрізки АВ і СD перетинаються в точці О, причому АО=ВО, СО=DО. Знайдіть кут ВDС і сторону АС, якщо 
DСА=70°, ВD=13 см.
Високий рівень (3 бали)
9.Дано рівні трикутники: ∆АВС=∆КМР, у трикутників ВН і МТ – відповідно їх бісектриси. Доведіть рівність ∆АВН=∆КМТ.
Контрольна робота №2 з теми «Ознаки рівності трикутників. Рівнобедрений трикутник»
Варіант 2
Початковий і середній рівень (6 балів)
1.Укажіть пару рівних сторін трикутників, якщо ∆МНК=∆ВСР
А)МН=РВ Б)МН=СР В)НК=СР Г)НК=РВ
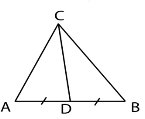
2.Визначте, яка з наведених рівностей випливає
з умови того, що у різносторонньому
трикутнику АВС відрізок СD є медіаною.
А)
САD=
СВD Б)АD=ВD В)АС=ВС Г)
АСD=
DСВ
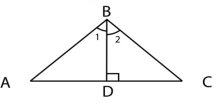
3.Визначте,за якими елементами два
трикутники, зображені на рисунку, рівні.
А)за двома сторонами і кутом між ними Б) за трьома сторонами
В)за стороною і прилеглими кутами Г)неможливо визначити
4.У трикутнику АВС АВ=6см, ВС=7см. Знайдіть периметр трикутника, якщо його бічною стороною є ВС.
А) 13см Б)15см В)19см Г)20см
5.У рівнобедреному трикутнику АВС ВС – основа, АD – медіана. Знайдіть кут ВАС, якщо 3
ВАD=90°.
А)30° Б)50° В)60° Г)90°
6.У трикутнику АВС АС=ВС, периметр трикутника дорівнює 80 см. Знайдіть АВ, якщо ВС=25 см.
Достатній рівень (3 бали)
7.Знайдіть сторони рівнобедреного трикутника, якщо його периметр дорівнює 100 см, а основа відноситься до бічної сторони, як 1:2.
8.Відрізки АВ і СD перетинаються в точці О, причому АО=ВО, СО=DО. Знайдіть кут ВСD і сторону ВС, якщо 
DСА=50°, АD=18 см.
Високий рівень (3 бали)
9.Дано рівні трикутники: ∆АВС=∆КМР, у трикутників ВН і МТ – відповідно їх медіани. Доведіть рівність ∆АВН=∆КМТ.
Контрольна робота №3 з теми «Паралельні прямі. Сума кутів трикутника»
Варіант 1
Початковий і середній рівень (6 балів)
1.Один з гострих кутів прямокутного трикутника 25°. Знайдіть інший гострий кут цього трикутника.
А)25° Б)45° В)65° Г)90°
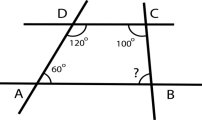
2.На рисунку 
А=60°, 
Д=120°,
С=100°. Знайдіть 
В.
А)60° Б)80° В)50° Г)70°
3.У ∆АВС 
А=33°, 
С=44°. Знайдіть найбільшу сторону цього трикутника.
А)АВ Б)ВС В)АС Г)неможливо знайти
4.Прямі а і в паралельні та перетнуті січною с, один з внутрішніх односторонніх кутів, що утворилися, у 3 рази більший за другий.
Знайдіть ці кути.
А)36°; 144° Б)45°; 135° В)50°; 130 Г)65°; 115°
5.У ∆АВС 
С=90°, 
В=60°, ВС=25 см. Знайдіть довжину АВ.
А)25 см Б)50 см В)30 см Г)60 см
6.Один з кутів, утворених при перетині паралельних прямих січною, дорівнює 138°. Знайдіть решту кутів.
Достатній рівень (3 бали)
7.У рівнобедреному ∆АВС з основою АС зовнішній кут при вершині В дорівнює 142°. Знайдіть кути трикутника АВС.
8.Кут при вершині рівнобедреного ∆АВС з основою АС дорівнює 78°. Знайдіть кут між основою трикутника та висотою, проведеною до бічної сторони.
Високий рівень (3 бали)
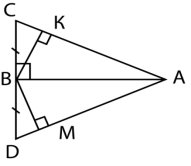
9.На рисунку ВС=ВД, ВК
АС,
ВМ
АД. Довести, що ВК=ВМ.
Контрольна робота №3 з теми «Паралельні прямі. Сума кутів трикутника»
Варіант 2
Початковий і середній рівень (6 балів)
1.Один з гострих кутів прямокутного трикутника 45°. Знайдіть інший гострий кут цього трикутника.
А)25° Б)45° В)65° Г)90°
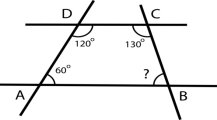
2.На рисунку 
А=60°, 
Д=120°,
С=130°. Знайдіть 
В.
А)60° Б)80° В)50° Г)70°
3.У ∆АВС 
С=33°, 
А=84°. Знайдіть найбільшу сторону цього трикутника.
А)АВ Б)ВС В)АС Г)неможливо знайти
4.Прямі а і в паралельні та перетнуті січною с, один з внутрішніх односторонніх кутів, що утворилися, у 4 рази більший за другий.
Знайдіть ці кути.
А)36°; 144° Б)45°; 135° В)50°; 130 Г)65°; 115°
5.У ∆АВС 
С=90°, 
В=60°, АВ=60 см. Знайдіть довжину ВС.
А)25 см Б)50 см В)30 см Г)60 см
6.Один з кутів, утворених при перетині паралельних прямих січною, дорівнює 68°. Знайдіть решту кутів.
Достатній рівень (3 бали)
7.У рівнобедреному ∆АВС з основою АС зовнішній кут при вершині В дорівнює 124°. Знайдіть кути трикутника АВС.
8.Кут між основою рівнобедреного трикутника та висотою, проведеною до бічної сторони, дорівнює 23°. Знайдіть кути цього трикутника.
Високий рівень (3 бали)
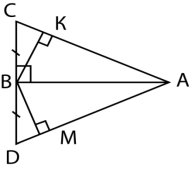
9.На рисунку ВС=ВД, ВКАС,
ВМАД. Довести, що АК=АМ.
Контрольна робота №4 з теми «Коло та круг»
Варіант 1
Початковий і середній рівень (6 балів)
1.Побудуйте коло з центром О і радіусом 2 см. Проведіть діаметр МР, хорду МК, радіус ОВ.
2.Дано коло з центром О, АК – дотична,
К - точка дотику, 
ОАК=32°. Знайдіть 
АОК.
А)32° Б)58° В)48° Г)90°
3.Точка Р лежить поза колом з центром О і радіусом 10 см. Яке з поданих тверджень є правильним:
А)ОР<10 см Б)ОР≤10 см В)ОР=10 см Г)ОР˃10 см
4.У якому випадку пряма а є дотичною до кола з діаметром 8 см, якщо пряма а віддалена від його центра на:
А)2 см, Б)3 см, В)4 см, Г)5 см?
5.Відомо, що АВ – діаметр, АС – хорда кола з центром О, 
ВОС=76°. Знайдіть 
АСО.
А)14° Б)76° В)90° Г)38°
6.Дано коло з центром О, ОС і ОD – радіуси кола. Знайдіть кути трикутника ОСD, якщо 
СDO=14°.
Достатній рівень (3 бали)
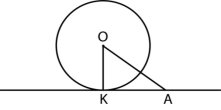
7.Пряма РК дотикається до кола з центром О
у точці А, АВ – хорда кола, 
АОВ=70°.
Знайдіть 
ВАК.
8.Коло, вписане в трикутник АВС, дотикається до його сторін АВ, ВС, АС в точках М, Р, К. Знайдіть периметр трикутника АВС, якщо АВ=10 см, МВ=4 см, РС=8 см.
Високий рівень (3 бали)
9.Дано коло, радіус ОК якого перпендикулярний до хорди СД. Знайдіть
СДК, якщо 
СОД=100°.
Контрольна робота №4 з теми «Коло та круг»
Варіант 2
Початковий і середній рівень (6 балів)
1.Побудуйте коло з центром О і радіусом 3 см. Проведіть діаметр МР, хорду МК, радіус ОВ.
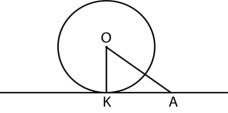
2.Дано коло з центром О, АК – дотична, К-
точка дотику, ОАК=42°. Знайдіть АОК.
А)32° Б)58° В)48° Г)90°
3.Точка Р лежить поза колом з центром О і радіусом 12 см. Яке з поданих тверджень є правильним:
А)ОР>12 см Б)ОР≤12 см В)ОР=12 см Г)ОР˂12 см
4.У якому випадку пряма а є дотичною до кола з діаметром 10 см, якщо пряма а віддалена від його центра на:
А)2 см, Б)3 см, В)4 см, Г)5 см?
5.Відомо, що АВ – діаметр, АС – хорда кола з центром О, ВОС=86°. Знайдіть ОАС.
А)43° Б)76° В)90° Г)38°
6.Дано коло з центром О, ОС і ОD – радіуси кола. Знайдіть кути трикутника ОСD, якщо ОСD=24°.
Достатній рівень (3 бали)
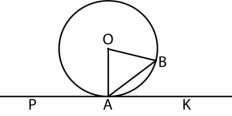
7.Пряма РК дотикається до кола з центром О
у точці А, АВ – хорда кола, АОВ=76°.
Знайдіть КАВ.
8.Коло, вписане в трикутник АВС дотикається до його сторін АВ, ВС, АС в точках М, Р, К. Знайдіть периметр трикутника АВС, якщо ВС=14 см, АК=7 см, РС=8 см.
Високий рівень (3 бали)
9.Дано коло, радіус ОК якого перпендикулярний до хорди СD. Знайдіть DСК, якщо СОD=88°
Контрольна робота №5 з теми «Повторення і систематизація навчального матеріалу»
Варіант 1
Початковий і середній рівень (6 балів)
1.Вкажіть, у якому випадку точки А, В і С не лежать на одній прямій.
А)АВ=14см, АС=8см, ВС=6см Б)АВ-5см, АС=11см, ВС=10см
В)АВ=18см, АС=6см, ВС=12см Г)АВ=8см, АС=14см, ВС=22см
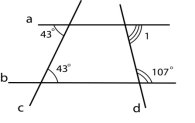
2.Знайдіть градусну міру кута 1,
зображеного на рисунку.
А)73° Б)63° В)43° Г)83°
3.Бічна сторона рівнобедреного трикутника дорівнює 15см,
а периметр – 50см. Яка довжина його основи?
А)35см Б)10см В)20см Г)25см
4.У трикутнику СКЕ відомо, що 
С=55°, 
К=110°. Укажіть правильну нерівність.
А)СЕ˂СК Б)СЕ˂КЕ В)КЕ˂СК Г)СК˂КЕ
5.Градусні міри суміжних кутів відносяться як 2:7. Яка градусна міра меншого з цих кутів?
А)80° Б)160° В)40° Г)140°
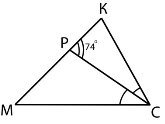
6.Відрізок СР – бісектриса трикутника, зображеного
на рисунку, 
МСК=60°. Яка градусна міра кута М?
Достатній рівень (3 бали)
7.На бічних сторонах АВ і ВС рівнобедреного трикутника АВС позначили відповідно точки D і Е такі, що 
АСD=
САЕ. Доведіть, що АD=СЕ.
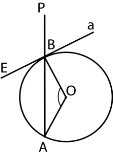
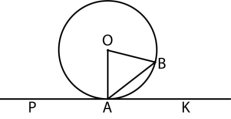
8.На рисунку пряма а дотикається до кола
з центром О в точці В. Знайдіть кут РВЕ,
якщо 
АОВ=122°.
Високий рівень (3 бали)
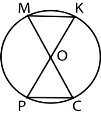
9.У колі з центром О, зображеному на рисунку,
проведено діаметри МС і КР. Доведіть, що хорди
МК і РС паралельні.
Контрольна робота №5 з теми «Повторення і систематизація навчального матеріалу»
Варіант 2
Початковий і середній рівень (6 балів)
1.Вкажіть, у якому випадку точки А, В і С не лежать на одній прямій.
А)АВ=10см, АС=4см, ВС=6см Б)АВ=17см, АС=14см, ВС=6см
В)АВ=5см, АС=7см, ВС=12см Г)АВ=16см, АС=8см, ВС=8см
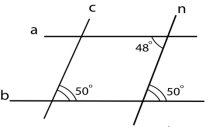
2.Які з прямих, зображених
на рисунку, паралельні?
А)а і в Б)с і п В)в і с Г)а і п
3.Основа рівнобедреного трикутника дорівнює 16см, а периметр – 56см. Яка довжина його бічної сторони?
А)20см Б)40см В)24см Г)12см
4.У трикутнику МРК відомо, що 
М=35°, 
Р=80°. Укажіть правильну нерівність.
А)МК˂МР Б)МР˂МК В)МР˂КР Г)МК˂КР
5.Один із суміжних кутів на 72° більший за другий. Яка градусна міра більшого з цих кутів?
А)54° Б)72° В)126° Г)140°
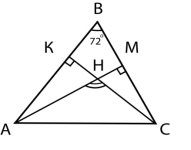
6.Відрізки АМ і СК – висоти трикутника АВС,
зображеного на рисунку, 
В=72°. Яка градусна
міра кута АНС?
Достатній рівень (3 бали)
7.На бічних сторонах АВ і ВС рівнобедреного трикутника АВС позначили відповідно точки М і К такі, що ВМ=ВК. Доведіть, що 
ВАК=
ВСМ.
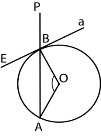
8.На рисунку пряма а дотикається до кола
з центром О в точці В. Знайдіть кут РВЕ,
якщо 
АОВ=110°.
Високий рівень (3 бали)
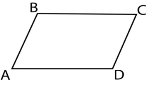
9.Доведіть, що відрізки АВ і СD, зображені на
рисунку, паралельні, якщо ВС=АD, ВСǁАD.
Відповіді
Діагностична контрольна робота з алгебри
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
В |
Г |
|
2 |
Б |
В |
|
3 |
А |
Б |
|
4 |
Г |
Г |
|
5 |
А |
Б |
|
6 |
Б |
В |
|
7 |
6а-8 |
2у_24 |
|
8 |
(4; 0) |
(-1; 0) |
|
9 |
54 і 18 |
30 кг і 6 кг |
Контрольна робота №1 «Лінійне рівняння з однією змінною»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
В |
Б |
|
2 |
Г |
Б |
|
3 |
Б |
Г |
|
4 |
Б |
В |
|
5 |
Б |
А |
|
6 |
9 і 17 |
24 кг і 8 кг |
|
7 |
6 |
-2 |
|
8 |
-37 |
13 |
|
9 |
20 км |
280 км |
Контрольна робота №2 «Степінь з натуральним показником. Одночлени»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
а)В, б)А, в)Б |
а)В, б)Г, в)А |
|
2 |
Б |
Г |
|
3 |
а)Б, б)В |
а)Б, б)Г |
|
4 |
а)Б, б)В |
а)А, б)Г |
|
5 |
Б |
Г |
|
6 |
а)-1, б)коренів немає |
а)1, б)коренів немає |
|
7 |
|
|
|
8 |
а)25, б) |
а)9, б) |
|
9 |
|
|
Контрольна робота №3 «Многочлени. Дії над многочленами»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
В |
В |
|
2 |
А |
Б |
|
3 |
Б |
А |
|
4 |
а)Г, б)В |
а)Б, б)А |
|
5 |
Б |
А |
|
6 |
Б |
В |
|
7 |
2,8 |
9,2 |
|
8 |
2а |
2 |
|
9 |
|
|
Контрольна робота №4 «Формули скороченого множення. Розкладання многочленів на множники»
|
№ п/п |
Варіант 1 |
Варіант 2 |
|
1 |
Б |
В |
|
2 |
Г |
В |
|
3 |
а)Б, б)В |
а)Г, б)А |
|
4 |
а)Б, б)В |
а)А, б)Г |
|
5 |
В |
А |
|
6 |
(у+в)(9х-в) |
(х-у)(7х+у) |
|
7 |
-10х-29 |
4х-13 |
|
8 |
а)-3; 3, б)5 |
а)-5; 2, б)-3 |
|
9 |
|
|
Контрольна робота №5 «Розкладання многочленів на множники різними способами»
|
№ п/п |
Варіант 1 |
Варіант 2 |
|
1 |
Б |
Г |
|
2 |
В |
Г |
|
3 |
В |
А |
|
4 |
3 |
-7 |
|
5 |
а)Г, б)Б |
а)А, б)В |
|
6 |
(х-2у)(3х-2) |
(х-2у)(4у-3) |
|
7 |
а)В, б)Г, в)А, г)Б |
а)В, б)Г, в)А, г)Б |
|
8 |
(6х+5т)² |
(4х-у)² |
|
9 |
а)(х-8)(х-2), б)(х+у-4)(х+у+4), в)а |
а)(х-14)(х+2), б)(х-у-3)(х-у+3)
в)т²( |
Контрольна робота №6 «Функції»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
Б |
Г |
|
2 |
Б |
Г |
|
3 |
Г |
Б |
|
4 |
а)Б, б)В |
а)Б, б)Г |
|
5 |
Б |
А |
|
6 |
|
|
|
7 |
(5; 0) (0; 35) |
(0; 42) (6; 0) |
|
8 |
-13 |
-5 |
|
9 |
|
|
Контрольна робота №7 «Системи лінійних рівнянь з двома змінними»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
Г |
Б |
|
2 |
Б |
В |
|
3 |
Б |
В |
|
4 |
В |
А |
|
5 |
В |
В |
|
6 |
Г |
Б |
|
7 |
(5; 1) |
(5; 1) |
|
8 |
(-2; 1) |
(2; 2) |
|
9 |
180г - 2%, 90г - 5% |
40грн книга, 30грн альбом |
Контрольна робота № 8 «Повторення і систематизація навчального матеріалу»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
Б |
А |
|
2 |
В |
Б |
|
3 |
Б |
Г |
|
4 |
Б |
А |
|
5 |
а)В, б)Б |
а)Г, б)А |
|
6 |
15 |
-3 |
|
7 |
(3; 2) |
(4; -5) |
|
8 |
у>0 прих˂2 |
у>0 при х˂-2 |
|
9 |
20 км/год, 15 км/год |
9 і 5 |
Контрольна робота №1 «Найпростіші геометричні фігури»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
А |
Г |
|
2 |
В |
Б |
|
3 |
В |
Б |
|
4 |
В |
А |
|
5 |
В |
Б |
|
6 |
36°, 144°, 144° |
72°, 108°, 108° |
|
7 |
65°, 35° |
30°, 70° |
|
8 |
24 см або 8 см |
22 см або 8 см |
|
9 |
63° або 37° |
96° або 150° |
Контрольна робота №2 «Рівність трикутників. Рівнобедрений трикутник»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
А |
В |
|
2 |
Г |
Б |
|
3 |
А |
В |
|
4 |
В |
Г |
|
5 |
В |
В |
|
6 |
45 см |
30 см |
|
7 |
40 см, 30 см, 30 см |
20 см, 40 см, 40 см |
|
8 |
70°, 13 см |
50°, 18 см |
|
9 |
|
|
Контрольна робота №3 «Паралельні прямі. Сума кутів трикутника»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
В |
Б |
|
2 |
Б |
В |
|
3 |
В |
Б |
|
4 |
Б |
А |
|
5 |
Б |
В |
|
6 |
3 кути по 138°, 4 кути по 42° |
3 кути по 68°, 4 кути по 112° |
|
7 |
36°, 71°, 71° |
56°, 62°, 62° |
|
8 |
49° |
67°, 67°, 46° |
|
9 |
|
|
Контрольна робота №4 «Коло та круг»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
|
|
|
2 |
Б |
В |
|
3 |
Г |
А |
|
4 |
В |
Г |
|
5 |
Г |
А |
|
6 |
14°, 14°, 52° |
24°, 24°, 132° |
|
7 |
35° |
38° |
|
8 |
36 см |
42 см |
|
9 |
25° |
22° |
Контрольна робота №5 «Повторення і систематизація навчального матеріалу»
|
№ п/п |
Варіант1 |
Варіант 2 |
|
1 |
Б |
Б |
|
2 |
А |
Б |
|
3 |
В |
А |
|
4 |
Г |
Б |
|
5 |
В |
126° |
|
6 |
44° |
108° |
|
7 |
|
|
|
8 |
61° |
55° |
|
9 |
|
|
Список використаних джерел
- Навчальна програма для загальноосвітніх навчальних закладів. Математика 5-9 класи. Програма затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804.
- Г. П. Бевз, В. Г. Бевз. Алгебра 7. – К.:»Генеза», 2015.
- А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. Геометрія 7. - Х.: «Гімназія», 2015.
- Збірник завдань для ДПА з математики, 9 клас. – К.: Центр навчально-методичної літератури, 2013.
- Л. Г. Стадник, О. М. Роганін. Алгебра 7. Поточний і підсумковий контроль. – Х.: «Ранок», 2010.
- А. Г. Мерзляк, В. Б. Полонський, Ю. М. Рабинович, М. С. Якір. Алгебра 7. Збірник задач і завдань для тематичного оцінювання. –Х.: «Гімназія», 2007.
- О. М. Роганін, Л. Г. Стадник. Геометрія 7. Поточний і підсумковий контроль. – Х.: «Ранок», 2010.
- А. Г. Мерзляк, В. Б. Полонський, Ю. М. Рабинович, М. С. Якір. Геометрія 7. Збірник задач і завдань для тематичного оцінювання. –Х.: «Гімназія», 2007.
1
про публікацію авторської розробки
Додати розробку
-
Книшоїд Ольга Леонідівна
12.10.2020 в 22:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Ковалевська Марія Антонівна
12.05.2020 в 09:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Глінчук Галина
06.11.2019 в 10:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Стрілець Наталія Василівна
17.10.2019 в 19:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-
Пурей Тетяна Альбертівна
24.06.2019 в 09:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука