розробка до уроку площі трикутників

                                       Урок №

                                (геометрія 9 клас)

Тема: Формули для знаходження площі трикутника

Мета уроку: повторення та закріплення вивченого матеріалу, сформувати поняття площі трикутників, знаходження площі трикутника, знаходження площі паралелограма застосування навичок для розв’язання прикладних задач

Тип уроку: засвоєння і вдосконалення нових знань і вмінь

Вимоги до рівня підготовки учнів: формують поняття площі трикутника ; застосовують формули для знаходження площі трикутника через дві сторони і кутом між ними, формули площі паралелограма через дві сусідні сторони і синус кута між ними, , формула площі довільного опуклого описаного многокутника, формула площі за радіусами вписаних  в трикутник, і описаних навколо трикутників кіл; і в який формули застосовують вивчені означення до розв'язування задач.

Хід уроку:

1. Перевірка домашнього завдання. Повторення теореми синусів, наслідки з неї, повторення теореми косинусів.
2. Історична довідка

Герон Олександрійський жив у другій половині першого століття нашої ери. Про Герона відомо досить мало. Однак до нас дійшли деякі його праці і копії його праць, на підставі яких Герона цілком заслужено вважають найвидатнішим інженером. Він винайшов автоматичні двері, які справляли величезне враження на людей, які приходили до храмів, перший торговий автомат, наливають за монетку певну кількість свяченої води, механічних співочих птахів, автоматичний театр,  арбалет, парову турбіну і багато іншого, а головне формулу Герона, яка дозволяє обчислити площу трикутника за довжинами його сторін, в дійсності була відкрита Архімедом. Однак це не применшує того, що зробила ця людина.

3. Формування знань

У 8-му ми знаходили площу трикутника знаючи його сторону і висоту проведену до неї ,  а також застосовували наслідок з даної теореми, що площа прямокутного трикутника дорівнює половині добутку катетів .

Теорема 1. ( формула площі трикутника за двома сторонами і кутом між ними) Площа трикутника дорівнює половині добутку двох його сторін на синус кута між ними.

Обчислюємо

                           Рис. 1

Наслідок. Площа паралелограма дорівнює добутку його сусідніх сторін на синус кута між ними.

(бо

Оскільки в рівносторонньому трикутнику всі кути площу трикутника можна знайти за формулою:

Теорема 2. (формула Герона) Площу трикутника  зі сторонами можна знайти за формулою:

*Довести дану формулу можна за теоремою косинусів.

Зі всіх формул випливає , (, що найбільша висота та, яка проведена до найменшої сторони і навпаки ,найменша сторона та яка проведена до найбільшої сторони.

         А як же ж знайти радіус кола описаного навколо трикутника?

За наслідком із теореми синусів маємо: де c сторона що лежити проти кута γ, звідси

Звідси знаходимо формулу описаного кола навколо прямокутного трикутника

Теорема 3 (формула площі трикутника за радіусом вписаного кола)

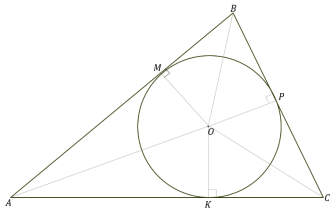
   півпериметр сторін трикутника  (рис.3)

Наслідок. Площу будь-якого опуклого многокутника можна знайти за формулою:

З доведеної формули випливає, що радіус кола вписаного в прямокутний трикутник дорівнює півсумі катетів без половини гіпотенузи:

Практичне застосування: в оптиці щоб найти фокусну відстань застосовують формулу площі зі променями і кутом відбивання між ними.

Домашнє завдання:

Висновок: Сьогодні ми вивчили як знаходити площу довільного трикутника, паралелограма, многокутника, в який вписане коло, розв’язали задачі на застосування даних формул.