Розробка індивідуального заняття з обдарованими учнями "Методи доведення нерівностей"

МЕТОДИ ДОВЕДЕННЯ НЕРІВНОСТЕЙ

Іноді в математичних задачах виникає необхідність довести, що нерівність з однією змінною є правильною для всіх значень змінної. Це роблять за означеннями понять «більше» або «менше»:

1) Число a більше від числа b, якщо різниця a–b є додатним числом.

2) Число a менше від числа b, якщо різниця a–b є від’ємним числом.

3) Число a дорівнює числу b, якщо різниця a–b дорівнює нулю.

Довести нерівність, що містить деякі змінні це значить показати, що дану нерівність задовольняють будь-які допустимі чи спеціально зазначені значення цих змінних. Доведення нерівностей зводиться звичайно до використання основних властивостей нерівностей і того, що x² ≥ 0 для всіх x R.

Для доведення нерівностей використовують різні прийоми та методи:

1.                     Доведення нерівностей на основі означення.
2.                     Метод застосування очевидної нерівності.
3.                     Метод застосування раніше доведеної нерівності [1, c.3].

 

Доведення нерівностей на основі означення

Цей прийом полягає в тому, що розглядають різницю лівої та правої частин нерівності і доводять, що ця різниця набуває значень постійного знака при будь-яких значеннях змінних. Зазвичай потрібно використати тотожні перетворення алгебраїчних виразів, розкладання на множники методом групування, методом виділення формули квадрата двочлена, тощо. Також використовуються властивості числових нерівностей: почленне додавання, множення та інші.

Приклад 1. Довести нерівність x³ + y³ ≥ xy(x + y), якщо x ≥ 0 , y ≥ 0 .

Розв’язання. Розглянемо різницю лівої і правої частин нерівності:

x³ + y³ – xy(x + y).

Виконаємо відповідні перетворення  x³ + y³ – x²y – xy² = x² (x – y) – y² (x – y) = = (x – y)(x² – y²) = (x – y)(x – y)(x + y) = (x + y)(x – y)² .

За умовою x ≥ 0 , y ≥ 0 , тому x + y ≥ 0, крім того (x – y)² ≥ 0 для будь-яких значень х та у, значить (x + y)( x – y)² ≥ 0.

Отже, x³ + y³ ≥ xy(x + y), що і треба було довести [1, c.3].

Приклад 2. Доведіть нерівність: a²b² + a² + b² + 4 6ab.

Розв’язання. Розглянемо різницю лівої і правої частин нерівності:

a²b² + a² + b² + 4 – 6ab.

Виконуємо тотожні перетворення одержаного виразу a²b² + a² + b² + 4 – 6ab = = a²b² – 4ab + 4 + a² – 2ab + b² = (ab – 2)² + (a – b)².

При будь-яких значеннях a і b ця різниця набуває тільки невід’ємних значень, отже, дана нерівність є правильною [5, c.196].

Приклад 3. Довести нерівність a² + b² + c² ≥ ab + bc + ac при будь-яких значеннях a, b, c .

Розв’язання. Помножимо ліву і праву частину нерівності на 2, маємо

2a² + 2b² + 2c² ≥ 2ab + 2bc + 2ac .

Розглянемо різницю лівої і правої частин нерівності та виконаємо перетворення:

2a² + 2b² + 2c² – 2ab – 2bc – 2ac = (a² – 2ab + b²) + (b² – 2bc + c²) + (c² – 2ac + a²) = = (a – b)² + (b – c)² + (c – a)² .

Оскільки (a – b)² ≥ 0, (b – c)² ≥ 0, (c - a)² ≥ 0, то різниця є невід’ємним числом.

Отже, a² + b² + c² ≥ ab + bc + ac  [1, c.4].

Приклад 4.  Доведіть, що коли a > b > c, то

Розв’язання. Маємо різницю лівої і правої частини:

.

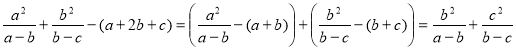Оскільки з умови a > b > c випливає, що a – b > 0, b – c > 0 і ,

то . Нерівність доведена [5, c.196].

 

Метод застосування очевидної нерівності

Цей прийом полягає в тому, що задану нерівність отримують у результаті перетворення очевидної нерівності чи додавання або множення кількох очевидних нерівностей. Очевидною зазвичай вважають нерівність (а – b)² ≥ 0 і подібні до неї.

Приклад 5. Доведіть нерівність: a² + b² + c² ≥ ab + bc + ca.

Розв’язання. Очевидно, що при будь-яких значеннях a, b і c виконується така нерівність:  (a - b)² + (b - c)² + (c - a)² ≥ 0.

Звідси a² - 2ab + b² + b² - 2bc + c² + c² - 2ca + a² ≥ 0;

a² + b² + c² ≥ ab + bc + ca [5, c.197].

Приклад 6. Доведіть, що коли a > 0, b > 0, c > 0, то

(a + b)∙ (b + c)∙ (c + a) 8abc.

Розв’язання. Для невід’ємних значень a, b і c виконуються такі три очевидні нерівності:

Звідси      

Оскільки обидві частини кожної з цих нерівностей набувають невід’ємних значень, то можна застосувати теорему про почленне множення нерівностей. Маємо:  (a + b)(b + c)(c + a)8.

Оскільки a > 0, b > 0, c > 0, то = abc. Отримуємо, що

(a + b)∙ (b + c)∙ (c + a) 8abc [5, c.198].

 

Метод застосування раніше доведеної нерівності

Нерідко раніше доведена нерівність може бути використана для доведення іншої, більш складної нерівності. Такими нерівностями можуть бути: , [5, c.197] для всіх чисел a і  b .

Приклад 7. Довести, що для будь-яких чисел a²+b²+c²ab+bc+ac.

Розв’язання. Згідно з раніше доведеною нерівністю , маємо:

a²+b²    2ab,   с²+b²    2сb,   a²+с²    2aс.

Додавши окремо ліві та праві частини нерівностей та поділивши обидві частини утвореної нерівності на 2 отримаємо a²+b²+c²ab+bc+ac.

Рівність досягається, якщо a=b=c [7, c.91].

Приклад 8. Довести, що при а ≥ 0, в ≥ 0 і с ≥ 0 виконується нерівність

ab(a + b)+ bc(b + c)+ ca(c + a) ≥ 6abc .

Розв’язання. Розкриємо дужки: a²b + ab² + b²c + bc² + c²a + ca² ≥ 6abc, тоді згрупувавши, маємо c(a² + b² ) + a(b² + c² ) + b(a² + c² ) ≥ 6abc .

Використаємо раніше доведену нерівність a² + b² ≥ 2ab, маємо:

c(a² + b² ) ≥ 2abc,   a(b² + c² ) ≥ 2abc,  b(a² + c² ) ≥ 2abc .

Додамо останні три нерівності c(a² + b² ) + a(b² + c² ) + b(a² + c² ) ≥ 6abc ,

отже ab(a + b)+ bc(b + c)+ ca(c + a) ≥ 6abc [1, c.5].

 

Доведення нерівностей другого степеня способом виділення квадрата двочлена або тричлена

Оскільки завдання на доведення нерівностей дуже різноманітні, то й способи доведення нерівностей різноманітні. Основний із них ― зведення заданої нерівності до рівносильної їй нерівності, права частина якої дорівнює нулю, і доведення того, що ліва частина нерівності набуває лише додатних, від’ємних, недодатних або невід’ємних значень.

При цьому важливо пам’ятати, що квадрат або парний степінь виразу набуває невід’ємних значень; якщо до квадрату або парного степеню виразу додається деяке додатне число, то одержаний вираз набуває лише додатних значень.

Приклад 9. Доведіть, що x² + 5y² + 4xy – 4y + 4 ≥ 0 при всіх дійсних значеннях x і y .

Розв’язання. Виділимо в лівій частині нерівності повні квадрати, маємо:

(x² + 4xy + 4y²) + ( y² – 4y + 4) = (x + 2y)² + ( y – 2)² , зрозуміло, що (x + 2y)² ≥ 0,

( y – 2)² ≥ 0, а значить (x + 2y)² + ( y – 2)² ≥ 0. Отже, при всіх дійсних значеннях x і y x² + 5y² + 4xy – 4y + 4 ≥ 0 [1, c.3].

Приклад 10. Доведіть нерівність та визначте, коли досягається рівність.

Розв’язання. Виділяємо квадрат тричлена та двочлена, подавши , тоді .

Здобутий вираз невід’ємний, бо є сумою двох невід’ємних виразів. Рівність нулю досягається лише за умови виконання рівностей

Звідки a = c, b = 3c.

Відповідь: нерівність доведена. Рівність досягається при a = c, b = 3c [7, c.92].

Приклад 11. Доведіть нерівність .

Розв’язання. Виділяючи квадрат тричлена та двочлена, маємо: , тобто , що справедливо [7, c.93].

 

Приклад 12. Доведіть нерівність .

Розв’язання. Виділяючи квадрат двочлена, маємо:

.

Оскільки обидва доданки невід'ємні, то й увесь вираз набуває невід'ємних значень.

Нерівність доведена [6, c.110].

 

Доведення нерівностей другого степеня за допомогою властивостей квадратного тричлена

Розглянувши усі описані вище методи доведення нерівностей, ми вирішили знайти свій метод для доведення нерівностей другого степеня. Многочлен другого степеня природно розглядати як квадратний тричлен відносно однієї зі змінних. Ідея прийому доведень із застосуванням властивостей квадратного тричлена полягає в наступному. Якщо при умові додатного першого коефіцієнта дискримінант квадратного тричлена є від'ємним числом, то можна стверджувати, що тричлен набуває лише додатних значень, а коли дискримінант дорівнює нулю, то невід'ємних значень при довільних значеннях змінних.

Правильними також є і такі міркування. Нехай утворено квадратний тричлен відносно деякої змінної, коефіцієнтами якого є вирази, що входять у дану нерівність. У випадку, коли встановлено, що він не має коренів, то дискримінант цього тричлена є від’ємним. Навпаки, якщо нам вдається показати, що корені є, то цим самим ми фактично обґрунтовуємо, що дискримінант квадратного тричлена не може бути від’ємним.

Покажемо використання першого з описаних прийомів.

Приклад 13. Доведіть нерівність та визначте, коли досягається рівність.

Розв’язання. Розглянемо ліву частину нерівності, як квадратний тричлен відносно b:                                          .

Знайдемо дискримінант утвореного тричлена:

;

.

Оскільки - невід’ємне число, то є недодатним числом, тобто D < 0 або D = 0

При D < 0 цей тричлен коренів не має і набуває лише додатних значень, тобто

.

При D = 0 тричлен набуває невід'ємних значень, тобто

.

Отже, для будь-яких значень a, b, c, що й треба було довести.

Рівність досягається якщо D = 0. При цьому .

Отже,  a = c, b = a + 2c.

Відповідь: нерівність доведена. Рівність досягається при a = c, b = 3c.

Розглянемо ще ряд прикладів на доведення нерівностей за допомогою вказаного методу.

Приклад 14. Доведіть нерівність .

Розв’язання. Розглянемо ліву частину нерівності, як квадратний тричлен відносно х:                                          .

Знайдемо дискримінант цього тричлена: ; ; .

Оскільки - невід’ємне число, тоді є від’ємним числом, тобто  D < 0.

Робимо висновок, що квадратний тричлен набуває лише додатних значень, тобто , що й треба було довести.

Приклад  15. Доведіть нерівність і з’ясуйте, коли досягається рівність:

.

Розв’язання. Розглянемо даний вираз, як квадратний тричлен відносно а. Знайдемо дискримінант цього тричлена: .

Очевидно, що D = -3 є недодатним числом, тобто  D < 0 або D = 0

У випадку D < 0 квадратний тричлен набуває лише додатних значень, тобто . У випадку D = 0 маємо, що .

Нерівність доведено.

Рівність досягається за умови:   

Отже, нерівністьправильна при будь-яких a, b. Рівність досягається при a = b = 0.

Приклад 16.  Доведіть нерівність і з’ясуйте, коли досягається рівність:

.

Розв’язання. Перетворимо дану нерівність:

;

.

Розглянемо ліву частину нерівності, як квадратний тричлен відносно a:

.

Знайдемо дискримінант відповідного тричлена:

; 

;  

.

Маємо, що  D < 0 або D = 0

Очевидно, що нерівність є правильною.

Рівність досягається при умові, що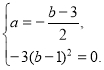

Отже, a = b = 1.

Приклад 17.  Доведіть нерівність і з’ясуйте, коли досягається рівність:

.

Розв’язання. Розглянемо ліву частину нерівності, як квадратний тричлен відносно x:                                          .

Знайдемо дискримінант цього тричлена:

;

.

Тоді D = -4 є недодатним числом, тобто D < 0 або D = 0 тому , що й треба було довести.

Рівність досягається в точці за умови, що , тому .

Покажемо використання другого з описаних прийомів.

Приклад 18. Довести, що для будь-яких , правильна нерівність .

Розв’язання. Якщо a = b = 0 , то нерівність очевидна. Нехай a + b > 0 . Зведемо дану нерівність до виду та розглянемо квадратне рівняння . Очевидно, що це рівняння має корені (зокрема коренем є значення x = 1). Тому дискримінант D рівняння задовольняє умову . Оскільки , то умова виконується, звідки отримуємо потрібну нерівність . Рівність можлива при рівних значеннях всіх змінних [1, c. 48].

Розглянемо інші приклади на доведення нерівностей другим прийомом.

Приклад 19. Довести, що при всіх виконується нерівність .

Розв’язання. Розглянемо квадратичну функцію

.

Знайдемо її значення в точках. Маємо:

;

.

Тоді після розкладання на множники одержимо та .

Тепер, оскільки при а ≠ b добуток , то можна стверджувати, що в точках функція приймає значення різні за знаком. Тому на відповідному проміжку існує корінь квадратного тричлена . Отже, його дискримінант додатний, а це доводить задану нерівність.

При а = b нерівність набуває виду або . Записавши її у вигляді (а - 1)²> 0, бачимо, що при а > 1 вона правильна [1, c. 49].

Приклад 20. Довести, що для всіх дійсних значень а виконується нерівність .

Розв’язання. Різницю можна вважати дискримінантом квадратного тричлена . Даний тричлен має корінь х = 1, тому його дискримінант не може бути від’ємним. Знак рівності можливий при а = 0 або а = 1.

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Барвінок Р.Л., Козлова О.М. Готуємося до математичних олімпіад та конкурсів разом Ч.III. – Черкаси: редакційно-видавничий відділ ЧОІПОПП, 2013. – 60 с.

2. Вороний О.М. Готуємось до олімпіади з математики. – Х.: Вид. група «Основа», 2008. – 255с.

3. Збірник завдань для державної підсумкової атестації з математики : 9 клас / Мерзляк А.Г. та ін.; за редакцією Бурди М.І.; - К.: Центр навч.-метод. л-ри, 2014. – 256 с.

4. Збірник завдань для державної підсумкової атестації з математики : 9 клас / Мерзляк А.Г., Полонський В.Б., Якір М.С. – Х.: Гімназія, 2019. – 160 с.

5. Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра. Підручник для загальноосвітніх навчальних закладів з поглибленим вивченням математики: підручник для 9 класу. – Х.: Гімназія, 2017. – 416с.: іл..

6. Сарана О.А. Математичні олімпіади: просте і складне поруч: Навчальний посібник. Друге видання, доповнене. – Тернопіль. Навчальна книга – Богдан, 2011. – 400 с.

7. Ушаков Р.П., Математичні етюди. Книга 2. – Х.: «Основа», 2008. – 140с.

 

 

Підготувала Минка Галина Володимирівна, вчитель математики Прилуцької гімназії № 1 ім. Георгія Вороного Прилуцької міської ради Чернігівської області