Урок "Співвідношення між тригонометричними функціями одного і того ж аргументу"
- Презентація.pptx pptx
- Хід уроку.docx docx
 Тема: «Співвідношення між тригонометричними функціями одного і того ж аргументу»
Тема: «Співвідношення між тригонометричними функціями одного і того ж аргументу»
Мета: 1) познайомити дітей з основними тригонометричними тотожностями, показати як застосовувати отриманні знання для виконання завдань, які містять тригонометричні функції;
2) розвивати в учнів уміння аналізувати, виділяти головне і робити висновки; у своїх роздумах користуватися дедуктивним методом від складного до простого; графічні навички;
3) виховувати в учнів наполегливість у подоланні труднощів, активну життєву позицію, здатність робити самооцінку своєї роботи.
Тип уроку: урок – подання нового матеріалу.
Хід уроку: І. Організаційна хвилина.
ІІ. Оголошення балів тестового д/з на Google Class.
Д/з на сьогодні у вас було у вигляді тестів на Google Class, отже, занесіть результати до листа самооцінки. На наступному уроці ми розберемо ті завдання, в яких була найбільша кількість помилок.
ІІІ. Оголошення теми уроку.
IV. Мотивація навчальної діяльності.
Перед вами хмаринка тегів у вигляді яблучка, яке буде емблемою сьогоднішнього уроку.
Серед англійців міцно вкоренилася фраза: «The apple you eat is the landscape you create», що дослівно перекладається так: «Яблуко, яке ви їсте, є навколишнє середовище, яке ви створюєте». Інакше кажучи, яблуко – це символ того, що людина сама творить свою долю й здатна своїми вчинками впливати на перебіг свого життя.
Сподіваюсь, що сьогоднішнє наукове яблучко спонукатиме вас, любі мої діти, на гарну працю на уроці.
V. Актуалізація базових знань.
Разом скуштуємо яблучко й повторимо основні поняття, якими ми будемо оперувати.
Мозковий штурм: тригонометрія, функція, графік, синус, косинус, тангенс, котангенс, тотожність, радіан, цілі числа.
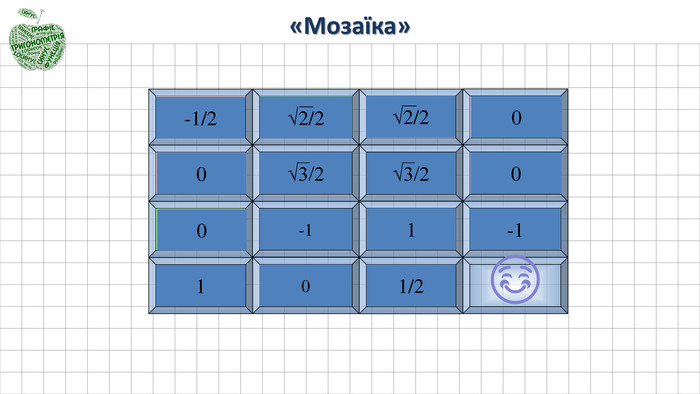
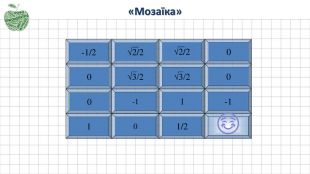
Продовжимо смакувати яблучком і виконаємо вправу «Мозаїка», де повторимо значення тригонометричних функцій деяких кутів.
VI. Пояснення нового матеріалу у вигляді евристичної бесіди.
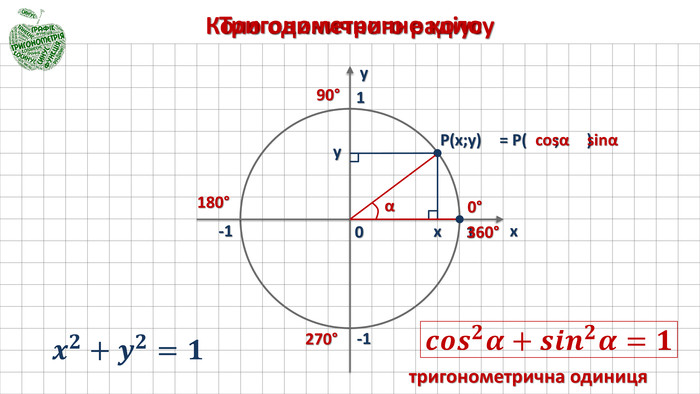
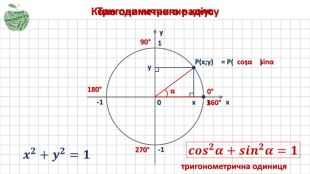
Розглянемо коло одиничного радіуса і оберемо точку Р(х;у) на колі:
- рівняння кола…(х2 + у2 = 1)
-
щоб коло стало тригонометричним, потрібно…
(в точках перетину кола з осями ординат розставити значення кутів повороту радіуса навколо початку відліку) - і ще…(замінити звичайні координати на тригонометричні функції)
- абсциса точки Р…(cosα)
- ордината точки Р…(sinα)
-
де α…
(кут повороту, в результаті якого з точки Р0(1;0) було отримано точку Р)
 Підставимо нові координати у рівняння кола:
Підставимо нові координати у рівняння кола:
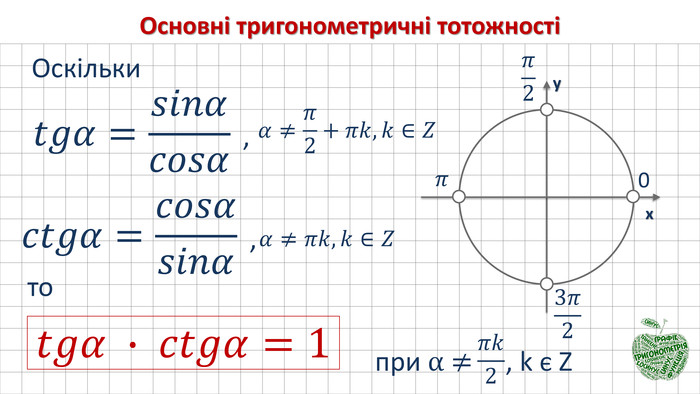
- отримаємо…(cos2α+sin2α=1) – основна тригонометрична тотожність. Використовуючи основну тригонометричну тотожність, знайдемо залежності між тангенсом і косинусом, а також між котангенсом і косинусом
- щоб отримати tg2α…(поділимо рівність на cos2α ≠ 0)
- ця тотожність є правильною…(при всіх α ≠ π/2 + πk, k є Z)
- щоб отримати ctg2α…(поділимо рівність на sin2α ≠ 0)
- ця тотожність є правильною…(при всіх α ≠ πk, k є Z)
-
знайдемо зв’язок між тангенсом і котангенсом…
(ця тотожність є правильною при…)
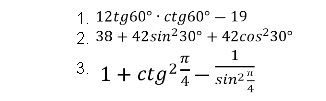
 Наприклад, виконаємо вправу на встановлення відповідності:
Наприклад, виконаємо вправу на встановлення відповідності:
![]()

![]()
Висновок…(я вважаю, що в даному випадку для економії часу доречніше скористуватися основними тригонометричними тотожностями, а не відомою таблицею деяких кутів тригонометричних функцій).
VII. Фізична розминка
Доречі, як ви вважаєте, чи можна визначити значення тригонометричних функцій деяких кутів, не запам’ятовуючи відому таблицю?.. А допоможе нам у цьому власна долоня! Існує так зване правило руки, або мнемонічне правило:
- якщо провести лінії через мізинець і великий палець, то вони перетнуться в точці, яка називається «місячний пагорб». Утворюється кут 90°.
- лінія мізинця утворює кут 0°.
- провівши промені з «місячного пагорба» через безіменний, середній, вказівний пальці, отримаємо кути 30°.45°,60° відповідно.
-
Підставляючи в формулу
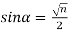 замість n 0, 1, 2, 3, 4 отримуємо відповідні значення синуса кутів 0°, 30°, 45°, 60°, 90°.
замість n 0, 1, 2, 3, 4 отримуємо відповідні значення синуса кутів 0°, 30°, 45°, 60°, 90°.
- для косинуса відлік відбувається у зворотньому порядку.
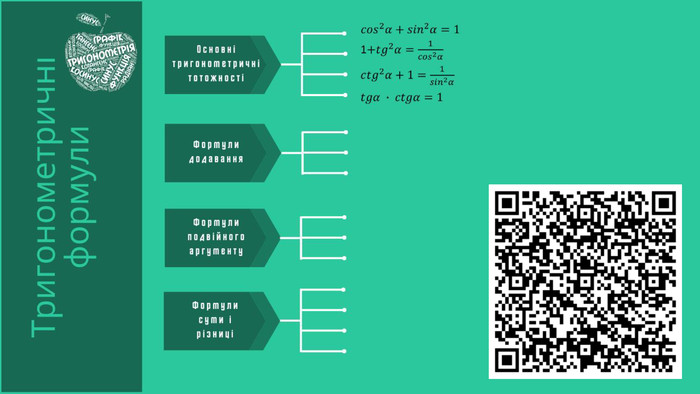
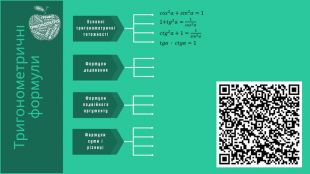
Отже, розпочнемо нашу накопичувальну скарбничку тригонометричних формул із занесенням основних тригонометричних тотожностей до інтелект картки. За допомогою мобільних телефонів скануємо QR код. За отриманим посиланням переходимо до інтелект картки. Таку картинку ви побачите у себе на екранах. Надалі ми будемо поповнювати інтелект картку новими блоками тригонометричних формул.
VIII. Відпрацьовування нового матеріалу.
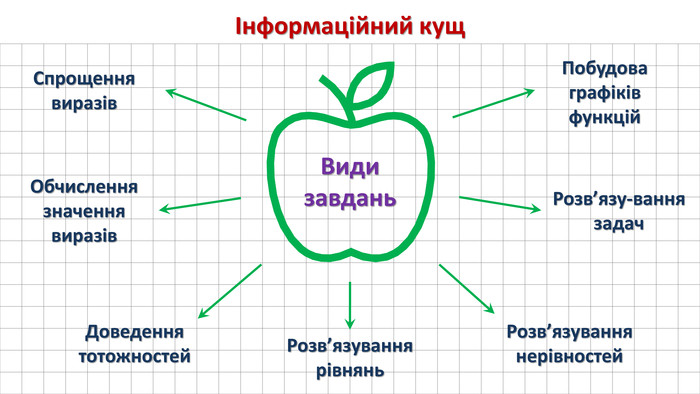
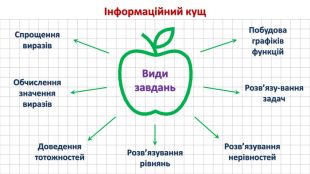
Продовжуємо відпрацьовувати набуті знання. Інформаційний кущ.
Види завдань з основними тригонометричними тотожностями:
- спрощення виразу
- обчислення значення виразу
- доведення тотожності
- розв’язування рівнянь
- розв’язування нерівностей
- розв’язування задач
- побудова графіків функцій
 Сьогодні ми опрацюємо деякі види цих завдань.
Сьогодні ми опрацюємо деякі види цих завдань.
Достатній рівень:
1) Чи можуть одночасно виконуватись рівності:
-
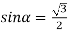 і
і 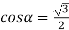 ; (ні)
; (ні)
-
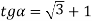 і
і 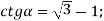 (ні)
(ні)
Обоснуйте
2) Знайти значення тригонометричних функцій аргументу α, якщо ![]() і
і ![]() .
.
Підвищений рівень:
3) Обчислити ![]() , якщо tgα = 5. (на ЗНО -1/2 = -0,5)
, якщо tgα = 5. (на ЗНО -1/2 = -0,5)
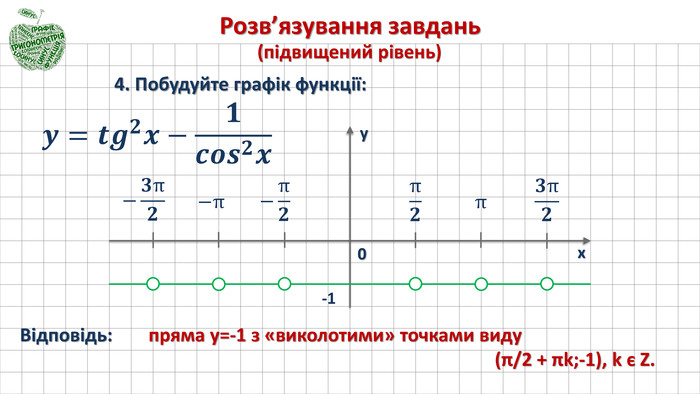
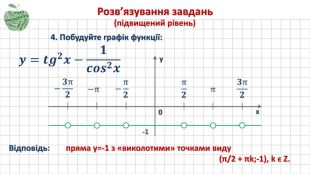
4) Побудуйте графік функції: ![]()
Відповідь: прямо у = -1, з якої «виколото» точки виду (π/2 + πk; -1), k є Z.
IX. Первинна перевірка засвоєного матеріалу.
Тестування за допомогою сервісу Plickers.
Переставили кількість здобутих балів до картки самооцінювання.
Х. Цікавинка.
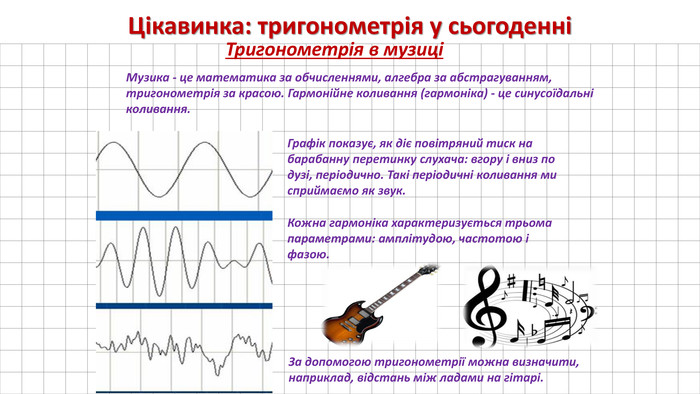
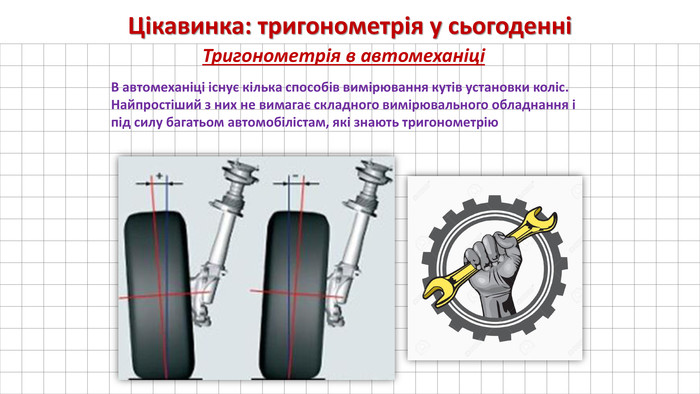
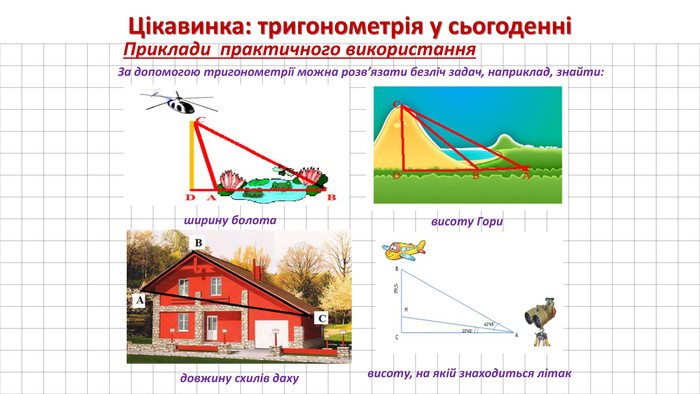
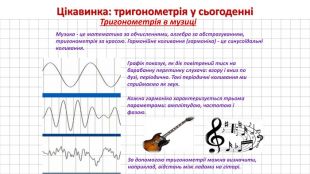
А поки ви підсумовуєте остаточну кількість балів і переводите їх в оцінки, я запрошую до виступу дівчат з міні-проектом: «Застосування тригонометрії у сьогоденні».
ХІ. Підсумки уроку. Поурочний бал.
Д/з: повт. п.22 №224(3); 22.10(1); 22.16(3); 22.18.
Зробимо підсумки, підніміть руки, хто отримав 11?...
ХІІ. Завдання-релакс.
На завершення смакування науковим яблучком пропоную закінчити речення:
-
Було цікаво дізнатись…
(що окрім звичайної одиниці існує ще й тригонометрична одиниця)
(де застосовується тригонометрія у сьогоденні) -
Мене здивувало…
(що існує зв’язок між розчепіреними пальцями руки і тригонометричними функціями кутів відомої таблиці) -
Мені сподобалось…
(яблучко тегів красиво виходить як реклама)
(інтелект-картка, дуже зручно, а ще весела думка, що на уроці можна було скористатися телефоном, а тебе за це навіть хвалять)
Так, з вами дійсно не засумуєш!
І на останок!
У британців є ще й такий вислів: «An apple a day keeps the doctor away», що означає «Одне яблуко на день позбавить від ліків», тобто завдяки насиченості цього фрукта корисними речовинами, можна забути про хвороби.
І ще: найвідоміші яблука це:
яблуко з Дерева Пізнання;
яблуко, яке спонукало Ньютона на створення закону всесвітнього тяжіння
і те яблуко, яке стало символом компанії Apple.
Доречі, найбільше яблуко важить 1,5кг і занесене до книги рекордів Гіннеса!
Дякую вам! Урок закінчено! (підніміться будь-ласка)
Любі діти, після корисного ланчу науковим яблучком, на перерві не забудьте вдягнути захисні маски!


про публікацію авторської розробки
Додати розробку