Розробка інтегрованого уроку з алгебри та фізики на тему "Застосування інтегралу при розв'язуванні задач з фізики"
Матеріал містить розробку інтегрованого уроку з фізики та алгебри на тему "Застосування інтегралу при розв'язуванні задач з фізики", а також вчительську та дві учнівські презентації до уроку.
- урок docx
- pptx
Департамент освіти і науки Вінницької обласної державної адміністрації
ДНЗ «Крижопільський професійний будівельний ліцей»
Інтегрований урок з алгебри та фізики на тему:
«Застосування інтегралу при розв’язуванні задач з фізики».
Бевза Людмила Семенівна
викладач математики, спеціаліст вищої категорії, відмінник освіти України, старший вчитель
Боровська Тетяна Іванівна
викладач фізики, спеціаліст вищої категорії, відмінник освіти України, старший вчитель
Інтегрований урок алгебри та фізики
Тема:Застосування інтегралу при розв’язуванні задач.
Мета:
навчальна-поглибити знання з теми «Інтеграл та застосування»; сприяти глибокому засвоєнню знань фізики і математики через встановлення міжпредметних зв’язків засобами інтегрального числення, формувати практичні навики розуміння законів, взаємозв’язків явищ у природі за допомогою розв’язування задач; формувати навички групової та індивідуальної роботи учнів; підготувати учнів до ДПА;
виховна- виховувати культуру розумової праці, виховувати прагнення до поглиблення та вдосконалення знань;
розвивальна— розвивати в учнів вміння узагальнювати цілісну систему, вміння реалізувати практичні зв’язки курсів математики і фізики, розвивати навички самостійного прийняття рішень, розвивати логічне і системне мислення, комунікабельність, відповідальність за роботу в команді при виконанні вправ.
Тип уроку: урок узагальнення і систематизації знань учнів.
Вид уроку:інтегрований урок математики та фізики, робота в групах
Дидактичне забезпечення: таблиці та роздавальний матеріал (додатки), тексти задач для розв’язання на уроці, проектор, ноутбук, портрети Архімеда, Ньютона, Лейбніца, презентація вчительська та учнівська.
Девіз уроку:
”Будь-яка наука тільки тоді
досягає досконалості, коли
вона користується математикою”.
Хід уроку
І.Організаційна частина
Урок супроводжується презентацією вчительською.
Вчитель математики:
Привітання. Перевірка готовності учнів до уроку.
Наш урок сьогодні інтегрований.
Змагаються дві рівносильні команди: команда «Інтеграл» та команда «Чомучки». Результати гри будуть заноситися в лист самооцінювання, який ви повинні зповнювати на протязі уроку. Кожне завдання оцінюється в 1 бал за правильність його виконання та 1 бал за швидкість.
Чомусь багато людей, особливо поети і лірики, кажуть, що наука математика суха, нудна. З такими епітетами, як точна, конструктивна, послідовна, я можу погодитися, але не з тим, що вона не цікава. Тому урок наш сьогодні незвичайний.Завдання нашого уроку – повторити визначення і формули первісної та інтеграла, розв’язати вправи на застосування цих формул.
ІІ. Мотивація навчальної діяльності.
В.фізики: Тема сьогоднішнього уроку – “Інтеграл та його застосування
під час розв’язування задач з фізики”. Часто, вивчаючи тему, учні запитують:
“А навіщоми це вивчаємо? Яке практичне застосування цього матеріалу?”
В.математ: Тому мета нашого уроку - поглибити знання з теми «Інтеграл та застосування»; сприяти глибокому засвоєнню знань фізики і математики через встановлення міжпредметних зв’язків засобами інтегрального числення, формувати практичні навики розуміння законів, взаємозв’язків явищ у природі за допомогою розв’язування задач; формувати навички групової та індивідуальної роботи учнів; підготувати учнів до ДПА;
В.фізики:Виявити зв’язок курсу математики з життям та іншими
навчальними предметами завжди є важливим і цікавим заняттям. Інтеграл належить до числа математичних понять, походження яких і розвиток, тісно пов’язано з розв’язуванням прикладних задач.Це поняття ми постараємось сьогодні застосувати в різних областях практичної діяльності людини, а саме: в фізиці, в біології, в економіці.
Зараз запрошуємо кожну команду продемонструвати презентації на тему «Екскурс в історію» та «Інтеграл – майстер обчислень» про актуальні проблеми нашої теми уроку, над пошуком яких ви працювали вдома.
(Кожна команда демонструє презентації)
В.математики Як бачимо, інтеграл – це ключ, який відчиняє ворота між
фізикою і математикою. Тут вони поєднуються в одне ціле. Фізика вивчає різні явища й процеси, які пов’язані зі змінним величинами, обчислювати які значно легше за допомогою інтеграла.
В. фізики Тому девізом нашого уроку стануть такі слова:
«Будь-яка наука тільки тоді
досягає досконалості, коли
вона користується
математикою».
ІІІ. Актуалізація опорних знань.
- Ми з вами познайомилися з іншим поняттям математичного аналізу без якого не збудувати сучасного будинку, космічного корабля, субмарини.
- Поняття інтеграл з'явилося в результаті практичної діяльності людини, використовується сьогодні в самих різних сферах науково-практичної діяльності людини, а саме: фізиці, хімії, біології, механіці, економіці. Тому на уроці ми будемо розв'язувати задачі прикладного характеру, що допоможе зрозуміти місце і роль математики в сучасному світі.
В. математ:Проведемо фізико-математичну розминку
І раунд «А ми це знаємо»
(Завдання роздано учням на листках, де необхідно знайти відповідну первісну для даної функції та встановити відповідність між формулою і фізичною величиною, з якою вона пов’язана, 7 балів):
Розминка “А ми це знаємо”
|
Функція |
С
|
хn |
|
SIN х |
COSх |
|
|
|
Загальний вигляд первісної |
|
|
|
|
|
|
|
Вчитель фізики: Повернемося до величин , які можна обчислювати за допомогою інтеграла. До них можна віднести: переміщення, роботу, масу, електричний заряд, тиск, теплоту, а також і геометричні величини – довжину, площу, об’єм.
ІІ раунд
«Знайди пару»
Установіть відповідність між формулою і фізичними величинами, які вона пов’язує.
1. s = ν(t) ∙ t A. Робота і потужність
2. A = N(t) ∙ t Б. Сила струму і електричний заряд
3. q = I(t) ∙ t В. Швидкість руху і переміщення 4. Q = c(t) ∙ t Г. Лінійна густина і маса стержня
Д. Кількість теплоти і теплоємність
За кожну вірну відповідь одержуємо 1 бал.
Перевіримо себе, дивлячись на екран.
|
|
1 |
2 |
3 |
4 |
|
А |
|
Х |
|
|
|
Б |
|
|
Х |
|
|
В |
Х |
|
|
|
|
Г |
|
|
|
|
|
Д |
|
|
|
Х |
В. математ: Щоб переконатись в тому, що ви дійсно знаєте даний матеріал,
проведемо роботу в групах під назвою “Пофантазуй”.
(після розв’язання, учні перевіряють один одного і виставляють
к-сть балів за роботу, звіряємо відповідь зі слайдом – 3 бали)
Знайти невизначений інтеграл:
а) ∫ 5cos x dх;
б) ∫ (4х3+7х2-3х-54) dх;
в) ∫ 8![]() dх.
dх.
Знайти невизначений інтеграл:
а) ∫ 7 Sinхdх;
б) ∫ (5х3-8х2+33х-9) dх;
в) ∫ 6![]() dх.
dх.
Відповіді
Знайти невизначений інтеграл:
а) ∫ 5cos x dх; (5sin x)
б) ∫ (4х3+7х2-3х-54)dх; ![]() (
(![]() )
)
в) ∫ 8![]() dх. (
dх. ( ![]() )
)
Знайти невизначений інтеграл:
а) ∫ 7 Sinхdх; (-7cos x)
б) ∫ (5х3-8х2+33х-9)dх; (![]() )
)
в) ∫ 6![]() dх.
dх. ![]() (
(![]() )
)
БЛІЦ-ТУРНІР Слайд14
В. математ:Щоб поновити знання про поняття площі криволінійної трапеції
та визначеного інтеграла проведемо гру під назвою
“Відшукай мене”
Слайд 15
( Вибрати ті інтеграли, які відповідають площам фігур, що
зображені на малюнках)
1) 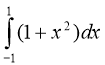 ; 2)
; 2) 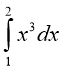 ; 3)
; 3) 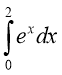 ; 4)
; 4) 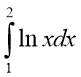 ;
;
5)  ; 6)
; 6) 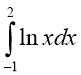 7)
7) 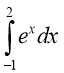 8)
8) 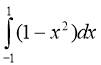
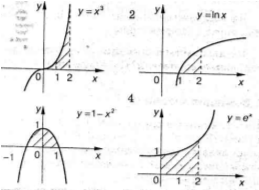
( відповіді на екрані )
В.фізики: Починаючи вивчати тему “Інтеграл”, ми спочатку розглянули задачі, які приводять до його поняття, а саме задачі з фізики. Слідуюча вправа має назву «Десь тут я є». Тому вам необхідно записати за допомогою інтеграла формули для обчислення:
1) шляху за відомим законом швидкості;
2) роботи змінної сили;
3) маси стержня;
4) кількості теплоти;
5) кількості електрики.
(На екрані за допомогою мультимедійного проектора відображається таблиця, а учням вона роздана на папері. Після її заповнення, учні звіряють з екраном і виставляють к-сть балів, 5 балів )
|
№п/п |
Величини |
Застосуванняінтегралу |
|
1 |
S - переміщення |
|
|
2 |
A - робота |
|
|
3 |
m - маса тонкого стержня |
|
|
4 |
q - електричний заряд |
|
|
5 |
Q - кількість теплоти |
|
( Відповіді на екрані)
|
№п/п |
Величини |
Застосуванняінтегралу |
|
1 |
S – переміщенняv -швидкість |
|
|
2 |
A– роботаF - сила |
|
|
3 |
m– маса тонкого стержня |
|
|
4 |
q– електричний заряд |
|
|
5 |
Q – кількість теплоти |
|
«ПОШТОВИЙ ЕКСПРЕС»
Вчитель фізики
Розглянемо приклади задач фізичного змісту, для розв’язання яких доцільно використати інтеграл. Для цього ви обираєте конверти із завданнями. Відкривши конверт ви знайдете метод, яким потрібно розв’язати задачу, математичний чи фізичний.
(Вчитель математики контролює правильність математичних дій)
Задача 1
Швидкість тіла υ з часом t змінюється за наступним законом: υ =2t+1
Знайти шлях, що пройшло тіло за четверту секунду свого руху.
Задача 2
Сила пружності пружини, розтягненої на 5 см, дорівнює 3Н. Яку роботу треба виконати, щоб розтягнути пружину на 5 см?
РОЗВ’ЯЗАННЯ
Задача 1
Обчислення шляху за відомим законом зміни швидкості
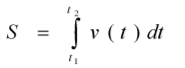
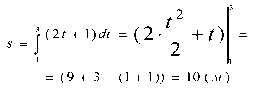
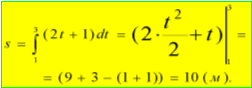
![]()
![]()
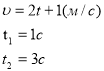
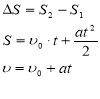
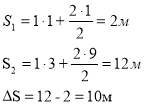
![]() S-?
S-? ![]()
Задача 2
Обчислення роботи змінної сили
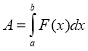
2. За законом Гука F=kx. З умови задачі випливає, що 3=k 0,05.
Отже, k = 60 і сила F=60x, а за формулой роботи змінної сили
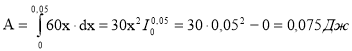
![]() F=3H А=Fх
F=3H А=Fх![]() ;
;
X = 5 cм За законом Гука F = кх, де к – коефіцієнт пружності і
![]()
![]()
A -? Середній тиск при розтягу пружини дорівнює півсумі тисків
на пружину в точці 0 і на відстані 0,05м. Тому відповідна сила
тиску буде ![]() , а робота
, а робота ![]()
![]()
![]()
Вчитель Фізики Ось ми і прийшли до конкурсу, який покаже наскільки уважними ми були впродовж уроку.
«ХТО ШВИДШЕ».
(Відповідь на екрані)
Підбиття підсумків, заключне слово викладача фізики.
Кожному учаснику з команди пропонувалось оцінити свого товариша за допомогою листа самооцінки.
Перехідна шкала оцінювання
5 балів – (10 – 13)
6 балів - (14-18)
7 балів - (19-21)
8 балів - (22 - 24)
9 балів - (25 - 27)
10 балів - (28 - 29)
11-І2 балів - (більше ніж 30)
Підбиття підсумків уроку. Виставлення оцінок
Заключне слововикладача математики.
На уроці було систематизовано знання щодо застосувань інтегралу при розв’язуванні прикладних задач.
- Тема «Інтеграл» яскраво демонструє зв’язок математики з фізикою, біологією,економікою і технікою. Розвиток сучасної науки немислимий
без використання інтегралу.
- В зв’язку з цим, вивчати його необхідно!
В. фізики: Як бачимо з проведеного уроку, що фізика вивчає залежності між величинами, але описує їх мовою математики. Ми зійшли на вершину гори, долаючи труднощі, виявляючи терпіння, наполегливість. На шляху нам зустрічалися явища, для розуміння і пояснення яких необхідні математичні знання.
Прочитайте фразу, написану на плакаті: "Забути не можна пам’ятати!" Від того, у якому місці ви поставите кому, матимете два варіанти: "Забути, не можна пам’ятати!" або "Забути не можна, пам’ятати!" На якому варіанті ви зупинитесь? Чи потрібні вам знання з математики в майбутньому?
Експрес – опитування
1. Що нового я дізнався на уроці?
2. Який етап уроку вам був найцікавіший?
3. Яке практичне застосування цього матеріалу?
4. Чи досягли ми поставленої мети?
5. Чи всі проблемні питання вдалося вирішити на даному уроці?
6. Чи сподобалася така форма роботи? На що варто звернути увагу вчителям
при організації таких уроків?
Консультанти заповнюють і здають листи оцінювання (додаються).
Домашнє завдання:
- Тіло рухається прямолінійно зі швидкістю v(t)=1-3t(м/с). Обчислити шлях, який пройшло тіло за інтервал часу від t1=2c, до t2=5с.
- Обчислити роботу, яку треба затратити, щоб викачати воду з циліндричної цистерни, радіус якої 2м, а висота 5м.
- Знайти масу неоднорідного стержня завдовжки 4см, якщо його густина змінюється за законом: ρ(l)=2l2+1 (кг/м3)
- Знайти кількість електрики, яка проходить через поперечний переріз
провідника за 20с, якщо сила струму змінюється за законом: I(t)=2t+1(A)
1

про публікацію авторської розробки
Додати розробку

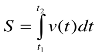
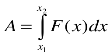
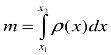
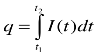
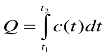







![Vт =∫ S(x) d x S=∫f(x) d x Через x є OX, x є [-R; R] будуємо переріз тіла площиною перпендикулярною (XOY) паралельно OY. Трикутник MNX- переріз. Трикутник MNX подібний трикутнику ABO: MN/AB=MX/AOMN/h= y/R, N (x; y; z), MN=h y /RSмn x=1/2 MN·MX= hy²/2 R, але M є колу x²+y²=R², т. е. y²=R²-x²S( x) = Sмn x= h (R²-x²) /2 RVтіла=2∫S(x)dx=2∫((R²-x²)h/2 R)dx=h/R(R²x-x³/3)| = h/R(R³-R³/3)=2h. R³/3 R=2/3h. R²Vв=Vц-Vк=πR²h-2/3 R²h=R²h/3(3π-2)Vв/Vк=3 π/2-1, отже не залежить від розмірів каструлі. Розв’язування задачі: Vт =∫ S(x) d x S=∫f(x) d x Через x є OX, x є [-R; R] будуємо переріз тіла площиною перпендикулярною (XOY) паралельно OY. Трикутник MNX- переріз. Трикутник MNX подібний трикутнику ABO: MN/AB=MX/AOMN/h= y/R, N (x; y; z), MN=h y /RSмn x=1/2 MN·MX= hy²/2 R, але M є колу x²+y²=R², т. е. y²=R²-x²S( x) = Sмn x= h (R²-x²) /2 RVтіла=2∫S(x)dx=2∫((R²-x²)h/2 R)dx=h/R(R²x-x³/3)| = h/R(R³-R³/3)=2h. R³/3 R=2/3h. R²Vв=Vц-Vк=πR²h-2/3 R²h=R²h/3(3π-2)Vв/Vк=3 π/2-1, отже не залежить від розмірів каструлі. Розв’язування задачі:](/uploads/files/61323/20452/20705_images/9.jpg)




























