Розробка інтегрованого уроку з геометрії та інформатики для 8 класу на тему "Розв'язування задач на обчислення площ многокутників"

Задача 1.         Задача 2.

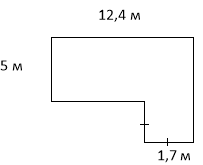Обчисліть площу земельної ділянки:

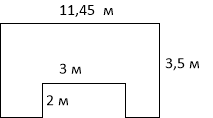
 Задача 3.         Задача 4.

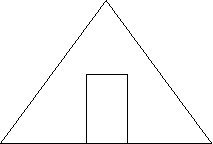
Обчислити площу частини фронтона    Обчислити форму фронтона 

будинку, яку треба пофарбувати, якщо    будинку, яку треба пофарбувати,

він має форму рівнобедреного трикутника   якщо він має форму рівнобічної

з основою 4,54 м і висотою 3,12 м,    трапеції з основами 5,16 м і 3,25 м

проведеною до неї. Розміри дверей, які    і висотою 3,16 м. Розміри дверей,

не фарбуються, вказано на мал.    які не фарбуються, вказано на мал.

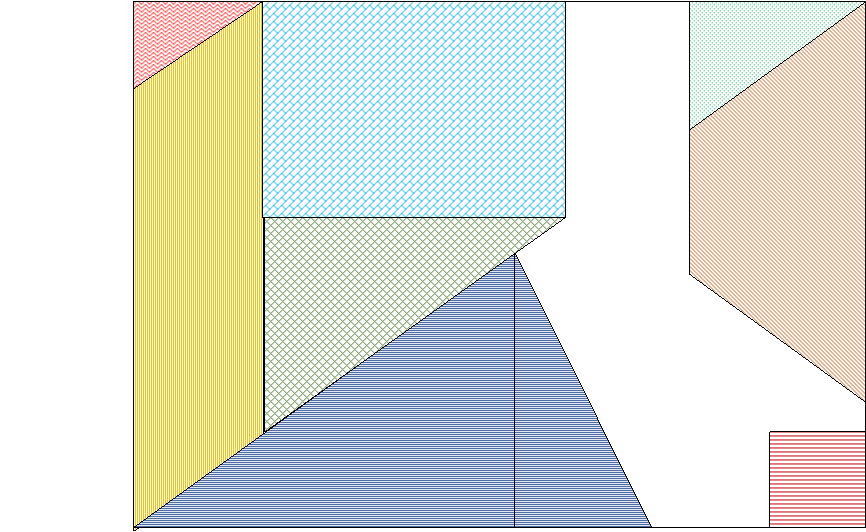
План паркових насаджень

V

V

План паркових насаджень

Тема:  Розв’язування задач на обчислення площ многокутників

Мета: закріплення в учнів навичок розв’язування типових задач з теми «Площі многокутників», навичок застосування програмних засобів для спрощення розрахунків при розв’язанні задач; формування навичок використання вбудованих функцій табличного процесора; розвиток уважності, логічного та  алгоритмічного мислення; виховання активності, самостійності, вміння працювати у групі, критично оцінювати свою роботу.

Обладнання: комп’ютери, ноутбук, проектор, роздавальний матеріал.

Тип уроку: застосування знань, умінь і навичок.

Перебіг уроку

І. Організаційний момент

Привітання, оголошення теми уроку

ІІ. Актуалізація опорних знань

• Бліц-контрольна

Учні отримують картки із завданнями на безпосереднє застосування формул площ многокутників. (Додаток 1) Картки лежать завданням донизу. За командою вчителя учні перевертають картки і на чистих аркушах розв’язують задачі: без пояснень, малюнки (якщо вони потрібні) – від руки. Отриману відповідь потрібно обвести.

За командою вчителя учні припиняють роботу, обмінюються аркушами з сусідом по парті для здійснення взаємоперевірки. Відповіді до задач проектуються на екран. За кожну правильну відповідь учні отримують один бал. Кількість набраних учнем балів вказується чітко, за потреби обводиться (для швидкої обробки результатів).

• Учитель просить підняти руку тих учнів, що набрали максимальну кількість балів за розв’язання контрольної роботи (якщо таких немає, то тих учнів, що допустили одну помилку). Ці учні отримують невеликі картки з цифрами 1, 2, 3, 4 – це майбутні лідери груп.

ІІІ. Мотивація навчальної діяльності 

На екран проектується умова задачі (Слайд 3). Учням пропонується завдання:

• складіть план розв’язання задачі (усно); (після відповідей учнів демонструється слайд (Слайд 4) з орієнтовним розв’язанням).
• оцініть складність завдання: на вашу думку, це задача, що відповідає середньому, достатньому чи початковому рівню?
• в чому може полягати складність при розв’язанні задачі? (Задача вимагає обчислень з десятковими дробами, і ці обчислення можуть вимагати більше часу, ніж самі міркування).

Висновок: іноді, коли при розв’язанні задачі необхідно швидко отримати результат, обчислення варто автоматизувати. Для цього можна використовувати як звичайний калькулятор, так і спеціальне програмне забезпечення.

• Назвіть прикладну програму, яка дозволяє автоматизувати і спростити розрахунки. (Табличний процесор)
• Чи правильно, що у формулах табличного процесора можуть використовуватися тільки числа? А що іще? (Посилання на клітинки, що містять необхідні для розрахунків числа)
• Чи доведеться для розв’язання даної задачі під час здійснення розрахунків в середовищі табличного процесора застосовувати вбудовані математичні функції? Які? (КОРЕНЬ)

IV. Застосування умінь і навичок

• Один з учнів (за бажанням) виконує необхідні для розв’язання задачі обчислення в середовищі табличного процесора (посилання на аркуш Excel з презентації) на ноутбуці. Результати проектуються на екран.
• Висновок: для розв’язання задачі треба знати відповідні формули, але обчислення значно спрощуються.
• Формули площ многокутників можна використовувати і для розв’язання задач у повсякденному житті. При цьому не має значення оформлення розв’язання задачі. Більше того, навіть не обов’язково знати напам’ять формули площ – їх можна знайти у довідковій літературі. У таких задачах важливий лише результат.
• Розв’язувати такі задачі вам допоможуть проекти, які підготували учні нашого класу. Це авторські роботи, які як раз і покликані автоматизувати обчислення, тому вам навіть не потрібно буде кожного разу вводити формули площ для здійснення розрахунків.

V. Захист учнівських проектів

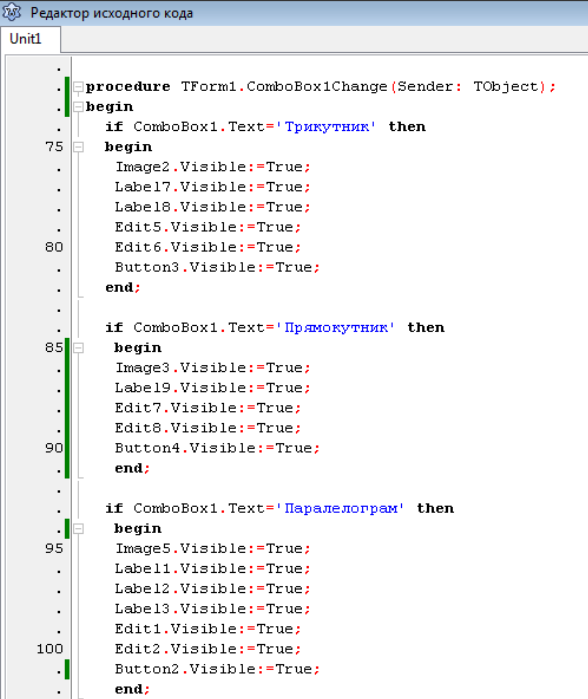
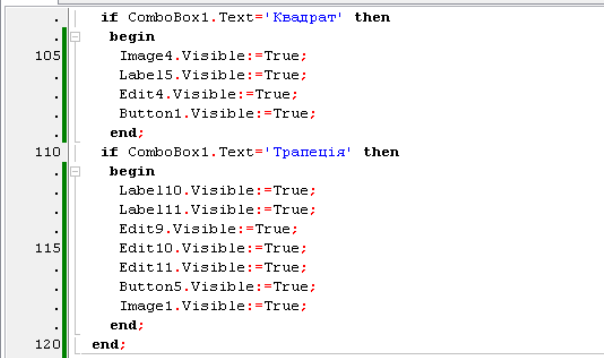
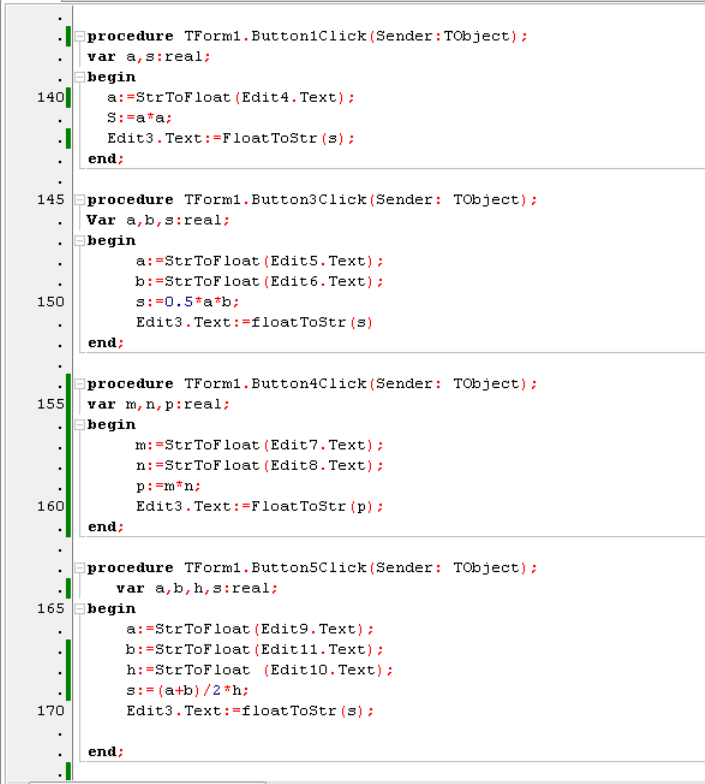
Учні представляють свої проекти, пояснюють принципи введення даних для обчислення площ  в кожному з них. Проект №1 створено у середовищі Excel, проект №2 – у середовищі візуального програмування Lazarus.

VI. Практичне застосування результатів проектної діяльності

• Учні об’єднуються у чотири групи: обирають навмання картку з цифрами 1, 2, 3, 4 і приєднуються до учня-лідера, що має картку з таким самим номером. (Крім того, на картках учнів є секретний код, призначення якого буде повідомлено пізніше). Учні-лідери, які набрали максимальну кількість балів (або помилилися один раз), призначаються консультантами: в ході роботи вони допомагають слабшим учням, вчать їх розв’язувати нескладні задачі на обчислення площ фігур.
• Наступне завдання учні виконують з використанням авторських проектів, які мають бути заздалегідь збережені на комп’ютерах, визначених для роботи груп.
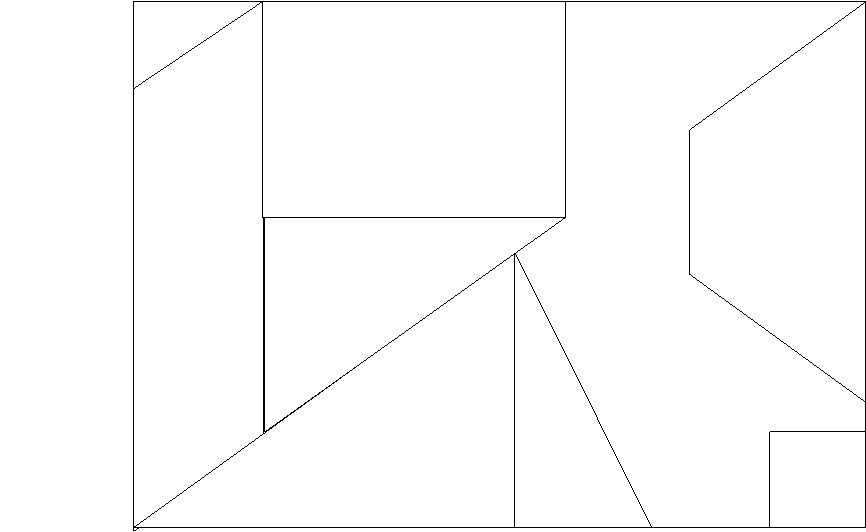
• Завдання «План паркових насаджень» (Додаток 2)

За вихідними даними слід визначити площу доріжки парку, яку треба викласти тротуарною плиткою.

Використовувати для виконання завдання доцільніше проект №1, оскільки він дає можливість виконувати і деякі проміжні обчислення. Обчислення площі доріжки базуватиметься на властивості площ: площа фігури дорівнює сумі площ фігур, з яких вона складається.

• Результати обчислень учні заносять до спеціальних бланків, потім групи звіряють результати, допомагають одне одному виправити помилки.
• Після того, як завдання виконано, учні обчислюють суму цифр секретного коду. У кожній групі буде учень, що одержить число 13. Саме ці учні демонструють своє вміння обчислювати площі многокутників (з використанням проекту №2). Навмання учні обирають одну з карток із задачею і показують її розв’язання за допомогою проекту №2. Процес обчислення проектується на екран. Правильна відповідь учня приносить бонусний бал усій групі.

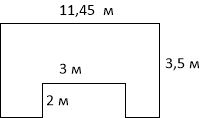
Задача 1.         Задача 2.

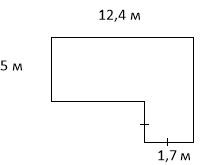Обчисліть площу земельної ділянки:

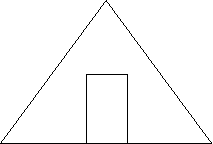
 Задача 3.         Задача 4.

Обчислити площу частини фронтона    Обчислити форму фронтона 

будинку, яку треба пофарбувати, якщо    будинку, яку треба пофарбувати,

він має форму рівнобедреного трикутника   якщо він має форму рівнобічної

з основою 4,54 м і висотою 3,12 м,    трапеції з основами 5,16 м і 3,25 м

проведеною до неї. Розміри дверей, які    і висотою 3,16 м. Розміри дверей,

не фарбуються, вказано на мал.    які не фарбуються, вказано на мал.

VIІ. Підсумок уроку

• Чого ви навчилися на уроці?
• Яке відкриття зробили для себе?
• (Класу демонструється програмний код Лазарус – код створеного учнями проекту). Як довго створювали даний проект? Коли доцільно використовувати створення такого роду проектів? (Коли планується розв’язувати велику кількість однотипних задач, інакше це не має сенсу)
• Рефлексія

Самооцінка роботи учня на уроці (іноді дуже важко бути чесним із самим собою, проте спробуємо це зробити).