Розробка позакласної роботи

Про матеріал

Збірник-практикум для позакласної роботи і можливо на уроках. Розкриті теми: усний рахунок, відсотки, софізми, задачі сільського господарства та цікаві математичні вечорниці.

Перегляд файлу

$C:\Users\Мокре\AppData\Local\Microsoft\Windows\INetCache\Content.Word\poster_1574510585655.jpg$
Мокренська загальноосвітня школа І-ІІІ ступенів

Дубрівської об’єднаної територіальної громади

Позакласна робота з математики

(практичні завдання з поясненням)

Мокре 2020

У роботі вміщено пояснення та завдання по темах: усний рахунок, відсотки, софізми та тематичний вечір. Секрети усного рахунку, можливо, допоможуть школярам рахувати без калькулятора. Завдання та пояснення по темах усний рахунок та відсотки, можуть бути використані як на уроках так і на гуртковій роботі.

Зміст

1. Передмова……………………………………………5

2. Як швидко навчитися рахувати усно……………….6

3. Відсоткові розрахунки……………………………..12

4. Задачі у сільському господарстві………………….21

5. Софізми……………………………………………...24

6. Математичні Андріївські вечорниці………………26

7. Список використаної літератури…………………..37

Передмова

«Зацікавити розум дитини – ось що є одним з основних положень нашої доктрини, і ми нічим не нехтуємо, щоб прищепити учневі смак та пристрасть до навчання.»

М.В.Остроградський

Мета - зацікавити учнів предметом. І тому перед вчителем математики постає завдання – допомогти учням сформувати бажання вчитися, розвинути в них позитивний мотив до навчання. Це питання є досить важливим і потребує кропіткої роботи для його втілення. Педагогу слід побачити в кожному учневі особистість, яка прагне до успіху, але успіх цей для кожного свій. Чим більше учень буде вірити у свій успіх, тим більше зусиль він докладатиме, тим сильнішою буде мотивація до навчальної діяльності. Якраз на позакласній роботі учні не бояться відповідати, тому що відповідь не оцінюється У разі очікування високого результату, за умови віри у свої здібності, у власні сили і можливості щодо подолання труднощів, посилюється почуття ефективності, яке спонукає працювати учня активніше.

Одним із засобів зацікавлення учнів математикою є добре продумана позакласна робота. Позакласні заняття дають можливість ширше пропагувати досягнення і значення математичної науки, прищепити учням любов до математики, сприяють виявленню і розвитку здібностей учнів, а також глибшому засвоєнню ними матеріалу. На таких заняттях можна організовувати розв’язування порівняння складних і цікавих задач, що розвивають кмітливість і математичне мислення, вивчати елементи історії математики, ознайомлення з життям і діяльністю славетних математиків. Тут створюється можливість для переконання дітей у тому, що саме через шкільну математику лежить шлях до широкого ознайомлення з досягненнями сучасної математичної науки, яка бурхливо розвивається.

На позакласних заняттях учні можуть дізнатися, що математика широко застосовується не лише в фізиці, хімії, астрономії але і в механіці, медицині, мовознавстві у багатьох галузях суспільних наук,найрізноманітніших галузях народного господарства. Велика роль позакласних занять і в справі прищеплення учнями навичок раціональних обчислень, вироблення в них смаку до усного обчислення.

Матеріали на математичний гурток.

І.Як швидко навчитися рахувати усно.

Щоб навчитися швидко рахувати усно, потрібно закласти міцний фундамент із самих простих математичних дій з невеликими числами. Важливо знати склад чисел від трьох до двадцяти

Для числа 3: 4: 5:

3=1+2 4=1+3 5=1+4

3=2+1 4=2+2 5=2+3

4=3+1 5=3+2

5=4+1

І так для всіх чисел до 10

Крім цього для швидкого рахунку потрібно натренуватися знаходити суми однакових доданків від одного до сотні

2+2=4 94+94=188

3+3=6… 95+95=190

І т. д. і т. д.

--------------- 99+99=198

21+21=42

22+22=44…

Також потрібно швидко ділити число на 2 для початку в межах двадцяти, а потім і в межах сотні.

Множення на 4 і на 8

Щоб помножити будь яке число на 4, його два рази подвоюють.

Наприклад:

112х4=112х2=224х2=448;

335х4=335х2=670х2=1340.

Щоб помножити довільне число на 8, його тричі подвоюють. Наприклад:

217х8=217х2=434х2=868х2=1736.

А можна іншим чином виконати множення на 8:

217х8=200х8+17х8=1600+136=1736.

Множення на 8 за методом Я. Трахтенберга виконується за такою схемою:

Перша цифра справа віднімається від 10 і подвоюється.
Середня цифра віднімається від 9 і подвоюється, потім додаємо сусідню цифру справа.
Віднімаємо 2 від крайньої зліва цифри більшого множника.

При цьому на початку віднімання перед більшим числом слід приписати нуль.

Наприклад: 789х8.

Крок перший. Віднімаємо від 10 дев'ятку і подвоюємо різницю. Одержуємо2.

Крок другий. Віднімаємо 8 від 9, подвоюємо різницю і додаємо 9 (крайню цифру справа). Одержуємо 11, записуємо зліва від двійки 1 і ще одну тримаємо в умі

Крок третій. Віднімаємо від дев'ятки 7, подвоюємо різницю додаємо 8 і одиницю із пам'яті одержуємо 13, записуємо 3 один тримаємо в умі.

Крок четвертий. Віднімаємо 2 від сімки і добавляємо одиницю з пам'яті, одержуємо 6

Відповідь: 6312.

Множення на 6.

За методом Якова Трахтенберга множення слідує таким чином додати до кожної цифри половину «сусіда», поставити на початку множника 0. При цьому потрібно брати до уваги, парними чи непарними записане дане число.

Розглянемо приклад в якому всі цифри парні: 244х6

Крок перший 4 крайня парна цифра даного числа, і так як «сусіда» в неї нема, то і додавати нема що:

Крок другий Друга цифра 4, її «сусід» -4. До чотирьох додаємо половину числа 4 (2) і одержуємо 6. Записуємо її біля 4.

Крок третій Наступна цифра 2 . Додаємо до 2 половину «сусіда» 2+2=4. Записуємо у відповідь.

Крок четвертий. Остання цифра зліва( в нашому записі) ---нуль. Додаємо до нуля половину числа2: 0+1=1. Записуємо 1 зліва від числа 4.

Відповідь:1464.

Повне правило множення на 6 таке: дописуємо зліва до великого множника 0, додати, починаючи з права, до кожної цифри половину «сусіда» і ще 5 в тому випадку, якщо цифра не парна.

Розв'яжемо такий приклад: 352х6

Цифри 3 і 5-- не парні. Тому, помножуючи цифри 3 і 5, ми повинні додатково додати 5 тільки тому, що вони не парні.

Крок перший. 2 – число парне і не має «сусіда» тому просто записуємо цю цифру

Крок другий Друга цифра 5 -непарна. Отже до 5 додаємо 5 і половину від 2, одержимо 11. На друге місце від 2 ми записуємо1 і ще 1 тримаємо в умі для переносу.

Крок третій. Три також непарне число. Тому 3 плюс 5 плюс половина від 5 (2,5 беремо ціле число, а десяті долі відкидаємо), плюс 1 із пам'яті – одержуємо 11. На третє місце зліва ми записуємо 1 і ще одиницю тримаємо в умі для переносу

Крок четвертий. Остання цифра зліва --нуль. Додаємо половину від числа 3 (1,5 беремо ціле число) додаємо 1 із пам'яті 0+1+1=2. Записуємо на крайню позицію зліва.

Відповідь :2112

Множення на 5 і 25.

Щоб помножити усно число на 5 потрібно поділити дане число на 2 і приписати нуль зліва. Наприклад:

36х5=(36:2х5.2)=18х10=180;

74х5=74:2х10=370;

43х5=43:2х10=21,5х10=215.

Щоб помножити число на 25, його спочатку ділимо на 4 (тобто пополовині і ще раз пополовині) і добавляємо два нулі( тобто множимо на 100) Наприклад:

36х25=(36:4 х 25х4)=9х100=900;

72х25=72:4х100=1800;

13х25=13:4х100=3,25х100=325.

Множення на 9

Множення на 9 за методом Трахтенберга виконується за правилом:

Записуємо перед множником нуль і віднімаємо праву цифру числа із 10 --- так ми отримуємо праву цифру результату.
Беремо почергово кожну цифру із слідуючих цифр до останньої, віднімаємо від 9 і додаємо «сусіда».
Коли будемо розглядати цифру нуль, яка стоїть перед даним числом, відніміть від «сусіда» і отримане число буде крайньою лівою цифрою результату.

Розглянемо для прикладу 769х9

Крок перший. Віднімаємо 9 від 10, одержуємо 1 і записуємо в крайню справа позицію.

Крок другий Віднімаємо 6 від 9 і додаємо сусідню цифру — дев'ятку . В результаті одержуємо 12, тому зліва від 1 ми пишемо 2 і 1 пам'ятаємо.

Крок третій 7 віднімаємо від 9(одержуємо 2 ), плюс сусідня шістка, плюс одиниця із пам'яті – одержуємо 9.

Крок четвертий. Нуль беремо, віднімаємо від 7 одиницю і записуємо 6 як результат.

Відповідь: 6921

Множення на 11

Щоб помножити число на 11 потрібно шукати суму крайніх цифр і ставити її в середину цифр числа.

34х11=374 (3 3+4 4);

25х11=275…(2 2+5..5);

63х11=693…(6 6+3..3);

68х11=748 (6+1 6+8 8 );

95х11=1045 (9+1 9+5 5);

633х11=6963 (6 6+3 3+3 3);

521х11=5731 (5 5+2 2+1 1);

845х11=9295 (8 8+4 5+4 5).

Додаткові хитрості усного рахунку.

Корисно запам’ятати:

37х3=111.

Запам'ятавши цю рівність, легко виконувати усне множення числа 37 на 6, 9, 12 і тому подібне;

37х6=37х3х2=222;

37х9=37х3х3=333;

37х12=37х3х4=444;

37х15= 37х3х5=555.

Корисно запам’ятати:

77х13=1001.

Запам'ятавши цю рівність, легко виконувати усне множення такого типу:

77х26=77х13х2=2002;

77х39=77х13х3=3003.

Корисно запам’ятати:

91х11=1001.

Запам'ятавши цю рівність, легко виконувати усне множення такого типу:

91х22=91х11х2=2002;

91х33=91х11х3=3003;

91х44=91х11х4=4004.

Корисно запам’ятати:

143х7=1001.

Легко обчислюються такі приклади:

143х14=143х7х2=2002;

143х21=143х7х3=3003;

143х28=143х7х4=4004.

Корисно запам’ятати:

125х8=1000.

^{125х16=125х8х2=2000;}

Легко обчислюються такі приклади:

125х24=125х8х3=3000; 125х32=125х8х4=4000.

Староруський прийом множення двох чисел.

Суть цього прийому полягає у тому, що один множник збільшували удвічі, а другий зменшували удвічі, поки один з них дорівнюватиме одиниці.

Наприклад: 27х16. Один співмножник ставили на початку одного стовпчика, а другий – на початку другого стовпчика і відповідно ділили навпіл доти, поки не отримували 1:

27 16

54 8

108 4

216 2

432 1

Отже, 27 х 16 = 54 х8 = 108 х 4 =216 х 2 = 432 х 1 = 432.

Квадрати чисел, які закінчуються 5.

Дуже легко підносити до квадрата числа, які закінчуються п’ятіркою.

15²=225 (першу цифру множимо на наступну в натуральному ряді 1х2 і дописуємо 25);

25²=625 (2 множимо на наступну 3 і дописуємо 25);

35²=1225 (3х4 25);

45²=2025 (4х5 25).

При вивченні способу добування квадратного кореня з числа учням можна продемонструвати математичний фокус, пов'язаний з добуванням кубічного кореня. Задумане число від 1 до 100 піднести його до кубу і не називаючи самого числа каже лише результат. Після цього вчитель негайно називає задумане число, тобто значення кубічного кореня з названого числа.

Для пояснення розглянемо таблицю кубів чисел від 1 до 10:

1³=1, 6³=216,

2³=8, 7³=343,

3³=27, 8³=512,

4³=64, 9³=729,

5³=125, 10³=1000.

Помічаємо, що всі куби чисел таблиці закінчуються різними цифрами. Отже знаючи цю таблицю, ми легко знаходимо цифру одиниць потрібного нам числа. Нехай , наприклад, задумане число, піднесене до куба, дало 140608. За таблицею знаходимо, що шукане число закінчується цифрою 2. Щоб знайти число десятків задуманого числа, ми довідуємося скільки тисяч є в числі 140608, тобто закреслюємо останні три цифри. Число 140 міститься (за таблицею ) між числами 125 і 216. Тому задумане число лежить між 50 і 60. Отже задумане число буде 52 (треба брати в таблиці менше з чисел між якими міститься 140). Зауважимо, що коли повідомлене нам число не перевищує 1000, то кубічний корінь з нього ми знаходимо безпосередньо з таблиці.

ІІ. Відсоткові розрахунки.

Велика кількість інформації яку подає світ, іде у відсотковому відношенні. Тому годин на засвоєння відсотків у шкільній програмі замало. У старішому підручнику з математики приділялося багато уваги темі відсотки. Вони були основним поняттям комерційної арифметики.

Тепер відсотки набули значно більшого поширення, але, як і раніше, ними користуються і в грошових розрахунках. А ще використовують у:

1) хімії (відсотковий склад розчинів,сполук);

2) біології (відсоток вологи, схожості);

3) фізиці (ККД, коефіцієнт тертя);

4) виробництві (відсоток виконання завдань);

5) статистиці; і т.д.

1. Слід запам'ятати:

1==0,01; 50=0,5;

10=0,1; 75=0,75;

25=0,25;

2.Три основні види задач на відсотки

І. Знаходження відсотків від даного числа.

В даних задачах маємо всю величину, потрібно знайти скільки цієї величини припадає на цікавлячи нас кількість відсотків.

Знайти 30 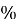від 400гр.

Перший спосіб: 400:100 =4гр. припадає на1

4х30=120гр.становлять 30

Другий спосіб: 30 =0,3

400х0,3= 120гр.

Третій спосіб (за пропорцією) 400гр ---100

Х гр. ------30 Х= =120гр.

Задача. У школі 1000 учнів, з них 55 -дівчата. Скільки дівчат у школі?

Розв'язання: 55 =0,55; 1000х0,55=550 дівчаток.

Відповідь: 550 дівчаток.

Задача. Прилад коштував 120гр. Він подешевшав на 10 На скільки гривень подешевшав прилад?

Розв'язання: 10 =0,1 120х0,1=12гр.подешевшав

Відповідь: на 12 гр.

ІІ. Знаходження числа за даними відсотками.

Такого типу задачі мають величину і її значення у відсотках, потрібно знайти всю величину.

Знайти число, якщо 20 становлять 60

Перший спосіб: 1) 60 :20 =3 становить 1

2) 3 х100 = 300

Другий спосіб: 20 = 0,2, 60 : 0,2 = 300

Третій спосіб: 20 _____ 60

100 _____Х Х = = 300

Задача Із жита отримують 75% борошна. Скільки жита треба змолоти, щоб отримати 20 кг. борошна?

Розв'язання: 75% = 0,75 20 : 0,75 = 27кг. жита необхідно взяти.

Відповідь: 27 кг.

Задача Під час сушки яблука втрачають 80% ваги. Скільки потрібно вяти свіжих яблук щоб одержати 30кг. сушених?

Розв'язання 100% - 80% = 20% (становлять сушені яблука)

20% = 0,2 30 :0,2 = 150кг. свіжих яблук потрібно

Відповідь:150кг.

Задача З молока виходить 25% вершків, а з вершків –20% масла. Скільки треба мати молока, щоб одержати 10 кг масла?

Розв'язання: Нехай молока Х кг, тоді вершків вийде 0,25х кг., а масла 0,25х .0,2 кг. За умовою масла має бути 10 кг. Складаємо і розв'язуємо рівняння:

0,25х . 0,2 = 10,

0,05х = 10,

х = 10: 0,05,

х = 200.

Відповідь: 200 кг молока.

ІІІ. Знаходження відсоткового відношення двох чисел.

Щоб знайти відсоткове відношення числа b до числа а, достатньо знайти їх відношення і помножити на 100%.

Задача : Знайти скільки відсотків становить 40 від 500

Перший спосіб: = 80%,

Другий спосіб: 40 --- х%

500 -------100% Х = =80%.

Задача. Потрібно зорати 300га землі. За перший день зорали 120 га. Скільки відсотків становить завдання виконаного за перший день?

Розв'язання:

Перший спосіб: 120 : 300 =0,4 = 40%.

Другий спосіб: 1) 300:100 = 3(га) припадає на 1%

2) 120:3 = 40 (%) становить 120га.

Третій спосіб: 300 га -------100%

120га ------- Х% Х = =40%.

Інші типи задач на відсотки.

ІV. Задачі на суміші та розчини.

У задачах на розчини вживається поняття «концентрація».

Означення. Якщо m – маса розчину, n – маса розчиненої речовини, то відношення n : m, подане у відсотках, називають концентрацією розчину.

Відсотковою концентрацією розчину називають виражене у відсотках відношення маси розчиненої речовини до маси всього розчину.

Задача 1: Під час змішування 30%-го розчину соляної кислоти з 10%-м одержали 600г 15%-го розчину. Скільки грамів кожного розчину було взято?

Розв'язання Перший спосіб Нехай 30%-го розчину взяли х г. Тоді 10 %-го розчину взяли (600 - х) г. У х г розчину міститься 0,3х г кислоти, в (600 - х) г міститься 0,1 (600 - х) г кислоти. А в 600 г розчину є 600 : 100 .15 = 90 (г) кислоти.

Одержимо: 0,3х + 0,1(600 -х) = 90,

0,3х +60 – 0,1х = 90,

0,2х = 30,

Х = 150.

Отже, 30%-го розчину взяли 150 г, а 10% -го взяли 600 – 150 =450 (г).

Відповідь. 150г, 450г.

Другий спосіб : Нехай 30%-го розчину взяли х г, а 10 % - у г. Тоді за умовою задачі х + у =600. У 30%-му розчині 0,3х г кислоти, у 10% -му розчині 0,1у г кислоти, а в 600 г 15 %-го розчину кислоти буде 600 :100 .15 =90 (г).

Отже маємо систему:

Відповідь: 150г, 450г.

Задача 2 : До 2 кг води долити 8 кг 70%-го розчину сірчаної кислоти. Визначити концентрацію утвореного розчину.

Розв'язання

1) 8 .0,7 = 5,6 (кг) чистої кислоти міститься у розчині сірчаної кислоти.

2) 2 + 8 = 10 (кг) – маса утвореного розчину.

3) 5,6 : 10 = 0,56 =56 % концентрація утвореного розчину.

Відповідь. 56 %.

Задача . 18%-й розчин солі масою 2 кг змішали зі стаканом води (0,25кг). Визначити концентрацію розчину, який отримали після змішування.

Розв'язання

Знайдемо, скільки солі знаходиться в 2 л розчину. Для цього складемо пропорцію:

2 кг ------100%,

Х кг--------18%,

звідси Х =

Після змішування з водою одержали розчин, маса якого

2 + 0,25 = 2,25 (кг).

Знайдемо відсоткову концентрацію розчину:

0,36 : 2,25 =0,16 = 16%

Задача. Змішали 60%-й розчин сірчаної кислоти з 25%-м розчином і отримали 700г 40%-го розчину. Скільки грамів кожного розчину було взято?

Розв'язання

Нехай 60%-го розчину взяли Х г, тоді 25%-го взяли (700- Х)г

У 700г 40%-го розчину міститься 700 . 0,4 = 280 (г сірчаної кислоти, в Х г розчину 0,6 г кислоти, а в (700 –х )г кислоти буде 0,25(700 –Х )г.

Одержимо: 0,6 + 0,25(700 - Х) = 280,

0,6Х +175 – 0,25Х = 280,

0,35Х = 105,

Х =300.

Отже, взяли 300 г 60%-го розчину. Тоді 25% розчину взяли 700 – 300 = 400 (г).

Відповідь. 300г, 400г.

Задача. У посудині є 30%-й розчин солі. Скільки кілограмів дистильованої води треба долити до 20 кг такого розчину, щоб концентрація солі зменшилася до 10%?

Розв'язання

Нехай Х кг – маса дистильованої води, яку треба долити

. Тоді ( 20 +Х) кг – маса утвореного розчину,

20 . 0,3 =6 (г) - вміст солі у 20кг 30%-го розчину,

(20 + Х).0,1 (г) - вміст солі у (20 + Х) кг 10%-го розчину.

Оскільки маса солі не змінилася, то маємо рівняння:

20 .0,3 = 0,1.(20 + Х),

20 + Х = 60,

Х = 40.

Відповідь. 40г.

V. Задачі на сплави.

Сплави можна розглядати як розчин, в яких один із компонентів (довільний) є розчинник, а другий – розчинена речовина.

Задача. Є сплав міді з оловом масою 12кг, який містить 45% міді. Скільки чистого олова потрібно додати до цього сплаву, щоб одержати новий сплав, який містить 40% міді?

Розв'язання

Вміст олова в сплаві масою 12 кг становить 55%, а у новому сплаві - 60%. Якщо до сплаву додати х кг олова, то олова в ньому, стане (12х055+ Х)кг. З іншого боку, у новому сплаві 0,6(12 + Х)кг олова.

Отже, маємо рівняння: 12х055+ Х) = 0,6(12 + Х),

6,6 + Х = 7,2 + 0,6х,

0,4х = 0,6,

Х =1,5.

Відповідь: 1,5кг.

Задача . Є сталь двох сортів, що містить нікелю відповідно 5% і 40%. Скільки сталі одного і другого сорту потрібно взяти, щоб одержати 140т сталі, яка містить 30% нікелю?

Розв'язання

Нехай треба взяти х т сталі, що містить 5% нікелю , та у т сталі, що містить 40% нікелю. Тоді безпосередньо нікелю у сплавах буде 0,05хт й 0,4у т. У 140т сталі нікелю буде 140х0,3 = 42(т).

Отже , маємо систему:

Х =100,

У =40.

Відповідь: 40т, 100т.

Задача. Сплав вагою 320кг містить 20% олова 144 кг свинцю. Визначити відсотковий вміст домішок.

Розв'язання

320х0,2 = 64 (кг) олова у сплаві.
144 +64 = 208 (кг)олова і свинцю у сплаві.
320 -208 = 112 (кг) домішок усплаві.
112 :320 =0,35 = 35% домішок

Відповідь: 35%.

Задачі для самостійного розв'язання

Із двох сплавів, що містять 60% і 80% міді, треба виготовити сплав масою 40кг з 75 %-м вмістом міді. Скільки кілограмів кожного сплаву треба взяти? Відповідь. 10,3 кг.
Сплав міді та цинку масою 36кг містить 45% міді. Скільки міді потрібно додати до сплаву, щоб одержаний новий сплав містив 60% міді?
Є три сплави. Маса першого становить 5 кг, а другого -3кг. Кожний з них містить 30% міді. Якщо перший сплав сплавити з третім, то одержимо сплав, що містить 56% міді, а якщо другий сплав сплавити з третім, то одержимо сплав, який містить 60 % міді. Знайти масу третього сплаву і відсоткову концентрацію міді в ньому.

Відповідь. 19кг, 69%

VI. Задачі на обчислення відсотків від відсотків.

Задача. Ціну товару спочатку знизили на 20%, потім ще на 15% і, нарешті ще на 10%. На скільки відсотків знизили початкову ціну товару?

Розв'язання

Нехай початкова ціна товару х грн., що становить 10%.

Тоді х-0,2х = 0,8х (грн.) – ціна товару після першого зниження;

0,8х – 0,15 . 0,8х = 0,68х (грн.) – ціна товару після другого зниження;

0,68х – 0,1 . 0,68х = 0,612х (грн.) – ціна товару після третього зниж.

Отже, усього ціна товару знизилася на

х – 0,612х = 0,388х (грн.).

Тому початкову ціну товару знизили на 38,8%.

Відповідь 38,8%.

Задача. Узимку ціна на молоко підвищилася на 20%, а на весні знизилася на 20%. Як змінилася початкова ціна молока?

Розв'язання

Нехай х – початкова ціна молока. Тоді 1,2х – ціна молока після її підвищення; 0,8 . 1,2х = 0,96х – ціна молока після її зниження;

Х – 0,96х = 0,04х – зміна ціни молока.

Отже початкова ціна молока зменшилася на 4%.

Відповідь. 4%.

VII. Задачі, у яких відомо, скільки відсотків одне число становить від другого.

Задача. Перше з невідомих чисел становить 140% від другого, а відношення першого до третього дорівнює Знайдіть ці числа, якщо різниця між третім і другим на 40 одиниць менша від числа, що становить 12,5% від суми першого і другого чисел.

Розв'язання

Нехай друге число дорівнює х. Тоді перше число дорівнює 1,4х, а третє - .1,4х = 1,1х.

За умовою задачі складаємо рівняння:

1,1х –х = 0,125(1,4х + х) -40 ,

0,1х = 0,175х + 0,125х – 40,

0,2х = 40

Х =200

Отже друге число дорівнює 200.

Тоді 1,4х = 1,4 .200 = 280- перше число;

1,1х = 1,1 .200 = 220 – третє число.

Відповідь. 280; 200; 220.

Поняття складних відсотків.

Вкладений в банк початковий капітал під р% річних через n років перетвориться в капітал

Це формула складних відсотків. Вона застосовується не лише у фінансових операціях, її використовують для знаходження кількості населення країни чи міста, зростання поголів’я тварин тощо.

Задача. Вкладник поклав у банк 200 000 грн. під 7% річних. Які відсоткові гроші він одержить через 5 років?

Розв'язання

За умовою початкова сума поетапно змінюється. При цьому кожного разу її зміна становить певну кількість відсотків від значення, яке ця величина мала на попередньому етапі. Нехай =200 000грн. – вихідне значення, яке змінюється на сталу кількість p % n разів, де p =7; n =5, тоді –сума через n років.

= 200 000 . = 200 000 . = 280510 (грн.)

Відсоткові гроші: 280510 200000 = 80510.

Відповідь: 80510 грн.

Задача. Від тривалого зберігання ячмінь втрачає за перший рік 3% своєї через 4 роки?

Розвязання

100 . 0,03 = 3 (ц) – втрати ячменю за перший рік зберігання

100 – 3 = 97 (ц) – маса ячменю після першого року зберігання.

Використовуємо формулу складних відсотків.

де p = 1%, n =3, = 97 ц.

Оскільки ячмінь втрачає у масі, то у формулі знак «-».

= 97 . =94.

Отже, через 4 роки від 100ц ячменю залишиться 94ц.

Відповідь: 94ц.

ІІІ. Задачі у сільському господарстві.

Визначення об'єму пального в бочках.

Є кілька випадків розв’язання цього завдання.

Випадок 1. Бочка повна стоїть на днищі. Об'єм визначають за формулою:

V = , де D – діаметр днища, H – висота бочки.

Діаметр і висоту легко визначити безпосереднім вимірюванням.

Випадок 2. Бочка стоїть на днищі неповна.

Об'єм визначають за формулою:

V = , де Н – висота стовпа пального в бочці.

Висоту Н вимірюють так: опускають дерев'яний стержень крізь отвір у бочку до дотикання з нижнім дном бочки (вертикально). Виймають стержень і вимірюють довжину його змоченої частини, яка й визначає висоту стовпа пального.

Випадок 3 Бочка лежить неповна.

Об'єм пального дорівнює об’єму тіла, висотою якого є висота бочки, а основою – круговий сегмент.

Для визначення об’єму треба знати площу кругового сегмента і висоту бочки L. Висоту бочки L вимірюють безпосередньо . Висоту сегмента визначають аналогічно до визначення Н у випадку 2.

При визначенні бочки для визначення об’єму використовують формулу: V = 2/3 x AHL, де А = 2²,

а R- радіус днища^.

При більшому наповненні бочки площу сегмента можна обчислити за формулою: S = , де - центральний кут, який спирається на дугу, що стягує хорду а.

Визначення ваги сіна в скиртах і стіжках.

а) Емпіричні формули для знаходження об’єму сіна в скиртах і стіжках, зокрема:

V = де П – довжина перекидки скирти; Ш – ширина скирти; D – довжина скирти в метрах;

V = , де П – довжина перекидки стіжка; L – довжина кола його основи.

Довжина перекидки дорівнює довжині шнурка, перекинутої через вершину скирти від її основи з одного боку до основи з протилежного боку. У деяких скирт перекидку вимірюють у двох-трьох місцях і беруть середнє арифметичне цих вимірювань. Ширину скирти вимірюють на висоті 1м від поверхні грунту на обох кінцях скирти. Ширину скирт, звужених біля основи, вимірюють з кожного боку біля поверхні землі і в найширшій частині. Суму цих вимірювань ділять на 4 і в результат вважають шириною скирти. Довжину вимірюють тільки з одного її боку.

Визначення ваги тварин

а ) Щоб визначити живу вагу коня, треба обхват за передніми ногами (в см) помножити на 6 і відняти 620;

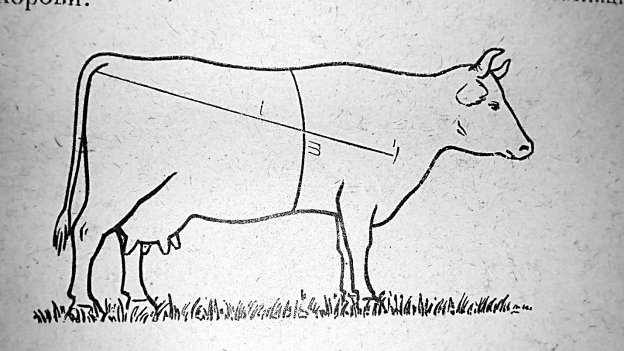
б ) Щоб визначити живу вагу корови, треба довжину (в см) по діагоналі тулуба (від кореня хвоста до передньої лопатки) помножити на довжину обхвату за передніми ногами і добуток поділити на 50;

в ) Щоб визначити живу вагу свині, треба довжину від потилиці до хвоста (в см) помножити на довжину обхвату за передніми ногами і добуток поділити: на 430 для вгодованих свиней, на 480 для свиней середньої вгодованості і на 530 для невгодованих.

Ознайомивши учнів з цими способами визначення ваги тварин, можна провести екскурсію на тваринницьке господарство, де практично перевіряють їх правильність.

Живу вагу корів, бичків, телят обмірюванням визначають ітак:

вимірюють обхват грудей m у см (на рисунку)
вимірюють похилу довжину l тулуба в см.

За цими двома числами знаходять у спеціальній таблиці вагу корови.

Наприклад, при m =180см. і l =175см у таблиці знаходимо Р =50кг.

l m	Похила довжина тулуба
l m	125	130	135	140	145	150	155	160	165	170	175	180	185
155	264	272	285	295	306	317	328
160	282	290	301	313	324	334	347	356
165		310	323	334	347	358	370	381	394
170			342	355	368	380	393	404	417	431
175				374	390	403	417	429	443	457	470
180					414	428	443	452	471	486	500	515
185						449	464	478	494	508	524	540	552
190							492	506	522	538	555	572	585

$C:\Users\Мокре\Desktop\20191119_213723.jpg$

Задача Обчислення врожайності пшениці на певній ділянці.

У = ,

де У –врожайність у ц/га; Р – вага в ц зібраної пшениці в бункері; в – ширина захвату жатки комбайна в м; а – довжина прокошеної комбайном смуги в м.

Задача Обчислення шляху, який пройде комбайн за час, поки його бункер наповниться зерном.

S = ,

де S – шуканий шлях; В – місткість бункера в ц; У – врожайність у ц/га; в – захват жатки комбайна в м.

^IV^{. Софізми}

^{Шукати щось завжди цікаво, а шукати помилку ще цікавіше.}^{Для цього в математиці}^{існують софізми.}

^Софізм^{(грецьке}^Sophisma^–^{вигадка, хитрість) –формально правильний, але хибний по суті умовивід, що ґрунтується на навмисно неправильному доборі вихідних положень у ланцюжку міркувань.}

^{1 софізм}

^{Відомо, що 2кг = 2000г, 3кг = 3000г.}

^{Перемножуючи}^{почленно, дістанемо : 6кг = 6000 000г.}

^{Виконуючи}^{ділення, матимемо :}^{кг =}^г.

^{2 софізм}^{«4 = 5»}

^Нехай^{а = в + с. Помножимо обидві частини на}^5:

^{5а = 5в + 5с.}

^{Додавши почленно цю рівність до рівності 4в + 4с = 4а}^{і віднявши від обох частин утвореної}^{рівності}^по^{9а, матимемо:}

^{4в + 4с – 4а =}^{5в +5с}^-5а,

^або^{4(в +с - а) = 5 (в +с - а).}

^{Звідси 4 = 5.}

^{3 софізм}^«^{Усі числа рівні між собою».}

^{Нехай, наприклад, а і в –два довільних числа і}^{а > в. Тоді знайдеться таке додатне число с, що а = в + с. Помножимо цю рівність почленно на а – в:}

^{аа – ав = ав +ас – вв –вс;}

^{аа – ав –ас = ав –вв –вс;}

^{а(а –в -с) = в (а –в -с).}^{Поділивши обидві частини останньої рівності на}^{а –в –с, дістанемо:}^{а = в.}

^{4 софізм}^«^{Сума будь-яких двох}^{однакових чисел дорівнює нулю}^».

^{Доведемо, що}^{а +а = 0. Нехай х = а. Помножимо обидві частини на}^{-4а, дістанемо:}^{-4ах = -4}^{, або}^{-4ах +4а = 0.}

^{Додамо до обох частин рівності}^{х; тоді}^х^{- 4ах + 4а = х, або (х -2а) = х, звідси х – 2а = х, звідки х – 2а = х. Але оскільки х = а, то а – 2а = а, тобто}^{- а = а.}

^{Остаточно: а + а =0.}

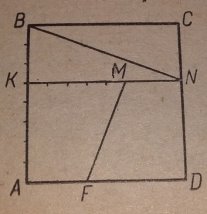
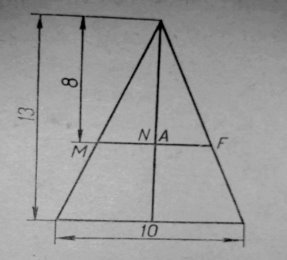
^{5 софізм}^{« 8 х 8 = 65»}

^{Дано квадрат}^ABCD^{, сторона якого дорівнює 8 одиницям.}^{У квадраті проведені прямі}^KN^,^MF^,^NB^{так як показано на рисунку. Ці прямі розбивають квадрат на 4}^{фігури. Дві}^{з них – рівні прямокутні трапеції і дві – рівні прямокутні трикутники.}^{З цих чотирьох фігур складаємо нову фігуру – трикутник (інший рисунок) Знаходимо площу цього трикутника}^{10 .13 :2 =65.}

$C:\Users\Мокре\Desktop\20191123_192928.jpg$ $C:\Users\Мокре\Desktop\20191123_193044.jpg$

V. Математичні вечорниці на Андрія.

Мета: ознайомити учнів з історією свята Андрія Первозванного; показати красу і велич українських народних свят, силу і магію чисел, виховувати в учнів любов до минулого до математики,шанобливе ставлення до українських традицій.

Обладнання: столи, калита, вареники коцюба,віхоть, сажа, «вічний календар»(до 3000 року), картки «Квадри долі», монети номіналом 2к. та 25к., модель годинника, бланки «Вивчення особистості»,ручки та аркуши паперу для кожного учня.

Господиня. Де ж це ті дівчата? Уже й стемніло, а їх немає. От ми, бувало… Як зачуєш, що вечорниці, то аж тини тріщать. Зранку ще біжимо, готуємося, бо ж хлопці прийдуть. А тепер? От чекають, доки ніч настане. Сядьмо, спочинемо трішки.

Подруга. А пам’ятаєш, як було ворожили на Андрія?

(Стук у двері. Чути сміх. Заходять дівчата.)

Перша дівчина. Добрий вечір, паніматко!

Друга дівчина. Чули , що у вас сьогодні вечорниці. Чи дозволите нам погуляти?

Господиня. Добрий вечір, дівчата! Заходьте, щоб щастя було в хаті, щоб я була багата. Я завжди рада гостям.

Третя дівчина. Давайте готувати вечерю, бо хлопці надійдуть.

Господиня. А де ваші хлопці?

Четверта дівчина. А самі почнемо вечорниці. Нехай їх завидки беруть! (Дівчата накривають столи: вареники поки що не ставлять.)

Пята дівчина. Дівчата, давайте повісимо калиту, доки хлопці не прийшли.

Шоста дівчина. Давайте! Тільки якнайшвидше! Хай поскачуть, а ми їх сажею вимажемо. (Підвішують до стелі калиту. Чути тупіт і стук у двері.)

Перша дівчина. Це хлопці, мабуть!

Перший хлопець (прсунувши голову у двері). Дівчата до хати пустіть , бо з дороги збився.

Друга дівчина. Гарненько попросіть, тоді пустимо. (Знову стук у двері.)

Третя дівчина. Кого там принесло ще? Хто такий?

Другий хлопець.Пес рябий, баран круторогий, ведмідь клишоногий. Пустіть до хати!

Четверта дівчина. Не пустимо в хату, бо дуже вас багато.

Перший хлопець. (грюкає.) Пустіть ліпше, а то буде гірше!

Пята дівчина. Як візьмемо рогатини, поламаємо ваші спини!

Другий хлопець. Дівчатоньки-голубоньки, та ми не прийшли сваритися, а погуляти. Гостинців вам принесли.

Шоста дівчина. Та заходьте вже, чого ж! Але лишень з піснею. (Хлопці заходять співаючи, вклоняються.)

Другий хлопець. Добрий вечір у вашій хаті! З Андрієм будьте здорові, дівчата, і Ви паніматко, і ви гості!

Господиня. Будьте й ви здорові. Ну, що ж , хлопці, сідайте в нашій хаті. (Хлопці сідають.)

Перший хлопець. А чого це сумно у вас, дівчата? А заспівайте всім нам.

Перша дівчина. А що заспіваємо, дівчата? (Дівчата співають українську пісню.)

Третя дівчина. А ми ще і не такої вміємо. (Починаються гумористичні переспівки між дівчатами і хлопцями)

Другий хлопець. Так співати ви вмієте. А от які з вас господині, чи вмієте ви біля печі ходити та їсти варити?

Друга дівчина. Та вже наварили! (Показує вареники.)

Хлопець. Та ще б скуштувати цих вареників. Може їх і собака їсти не захоче?

Господиня. Наші дівчата все вміють! А тепер покажіть, на що ви здатні. Хлопці здавна на вечорницях розказували смішні історії. А чи вмієте розсмішити та розвеселити дівчат? (Хлопці розповідають народні усмішки.)

Пята дівчина. А що наші хлопці заробили вареників?

Дівчата. Заробили, заробили. (Дівчата виносять вареники, всі їх їдять, веселяться та жартують.)

Шоста дівчина. Побачимо , які наші хлопці спритні. А ну ж бо, хто хоче калиту кусати?

Перший хлопець. Їду, їду калиту кусати!

Перша дівчина. А я буду віхтем сажею розмальовувати.

Перший хлопець. А я вкушу! (Їде на коцюбі і намагається вкусити калиту, а дівчина маже його сажею. Так по черзі до тих пір, поки хтось не вкусить калиту. Потім подруга господині ламає калиту і роздає всім.)

Господиня (під час гри наспівує пісню.)

Анаша калита, та з маком і медом,

Йди до неї, кусай її зверху і знизу.

Йди до неї кусай її, сторони не бійся,

Кусай, кусай калиту, але не засмійся.

Йди до неї, кусай її, назад повертайся,

Як вдалося відкусити – пари сподівайся!

Друга дівчина. Дівчата, сьогодні ж ворожать! Давайте і ми поворожимо на долю.

Хлопець. А ми також хочемо знати свою долю!

Подруга. Ось вам роздають картки «Квадри долі.» Виконайте дії, що вказані на першій картці, а потім на другій – прочитайте кожен про себе, залежно від кількості отриманих однакових цифр. (У дужках пропонуємо зразок виконаних дій для людини, яка народилася 5 вересня 1967 року.)

Картка 1. Квадри долі

Запишіть дату свого народження: число (двома цифрами), місяць (двома цифрами), рік (чотирма цифрами). 05 09 1967
Знайдіть суму всіх восьми цифр. 0+5+0+9+1+6+7=37
Знайдіть суму цифр отриманого числа. 3+7=10
Запишіть у першому рядку вісім цифр, що є датою вашого народження, у другому – поряд результати другої і третьої дій 05091967

3710

Від числа, що ви отримали у другій дії, відніміть подвоєну цифру першого рядка. ( З7-2.0=37
Додайте цифри отриманого числа. 3+7=10
Допишіть у другий рядок четвертої дії числа, що є результатами п’ятої та шостої дій.

05091967 ( 37103710

Порахуйте, скільки і яких однакових цифр є у вашому запису. (1-три, 2-немає, 3-дві, 4-немає, 5-одна, 6-одна, 7-три, 8-немає, 9-дві.)

Картка2. Квадри долі

Кількість «1» визначає характер людини:

одна-егоїстична людина, що в будь-який ситуації намагається отримати максимальну вигоду;

дві- схильна до егоїзму людина, яка потребує постійної похвали від сторонніх;

три – «золота серединка», комунікабельна людина зі спокійним характером;

чотири – людина з сильним вольовим характером; чоловіки - прекрасні вояки, а жінки – лідери у сімї;

п’ять – людина-диктатор, що не озираючись і не спиняючись прямує до своєї мети; разом з тим, дуже любить своїх дітей та онуків;

шість – жорстока людина, але здатна здійснити неможливе заради своїх близьких.

Кількість «2» визначає біоенергетику людини

немає – біоенергія на досить низькому рівні; любить книги, антикваріат, добре вихована людина, уважна до оточуючих.

одна- біоенергії мало; відчуває зміни погоди;має уникати стресових ситуацій; варто займатися спротом.

дві – людина має відносно великий запас біоенергії; гарний лікар та медична сестра

три –людина, що може лікувати за допомогою свого біополя;для розвитку здібностей потрібен незначний поштовх;

чотири – якщо ви зустріли дівчину, в яку закохані всі хлопці, або хлопця, у товаристві якого починає тріпотіти дівоче серце, то напевне у цієї людини є чотири двійки.

«3»-визначає внутрішній склад людини:

немає- дуже пунктуальна людина; жінки- чудові господині, чоловіки ретельно стежать за своїм зовнішнім виглядом;

одна – людина настрою, не любить економити; у її домі – то жахливий безлад, то ідеальна чистота;

дві –людина з аналітичним складом розуму, схильна до наук;

три і більше – людина з підвищеною схильністю до наук.

«4» визначає здоровя людини:

немає - здоровя слабке;

одна –щоб бути здоровою людиною, обов’язково слід загартувати організм;

дві – людина з міцним здоровям;

три і більше – дуже міцне здоровя; чоловіки розвинені фізично.

«5» визначає інтуїцію:

немає – канал зв’язку з тонким світом, з космосом закритий; людина постійно зайнята розрахунками, експериментами, намагається щось комусь довести;

одна - така людина робить мало помилок, може розрахувати ситуацію і отримати від неї максимальну користь;

дві –людина має дуже розвинену інтуїцію; непоганий фізіономіст;

три – майже провидиця; практично не допускає помилок у житті;

чотири – людина-провидиця, іноді знаходиться поза часом і поза простором.

«6» визначає ступінь приземленості людини:

немає – людина має неабиякий художній смак,фантазію , неординарну уяву; може оволодівати різними ремеслами;

одна – однаково успішно може займатися як точними, так і творчими науками;

дві – у людини переважають духовні складові, але фізична праця є обов’язковою умовою існування;

три – бажана розумова діяльність або заняття мистецтвом;

чотири – людина підвищеного темпераменту, приваблива, завжди в центрі уваги;

п’ять – людина дуже багато працює і не уявляє свого життя без цього.

«7» визначає міру таланту людини:

одна-людина народжена щоб доводити існування таланту у життєвих випробуваннях; чим більше людина такого типу працює, тим більше отримує в майбутньому;

дві- знак «ангелоподібності» , якщо розвинути йог повністю; людина дуже обдарована, схильна до музики, має тонкий художній смак;

три – людина добра і безтурботна, але хворобливо сприймає будь-яку несправедливість.

«8»визначає почуття обов’язку людини:

немає- майже повна відсутність почуття відповідальності;

одна – людина відповідальна, добросовісна, пунктуальна;

дві – у людини розвинуте почуття обов’язку;

три – знак великого обов’язку, знак служіння народу;

чотири – людина з парапсихологічними здібностями і винятковою сприйнятливістю до точних наук.

«9» визначає інтелект людини:

одна – людина мусить наполегливо працювати, щоб заробити ще одну «9»;

дві - людина розумна від народження, вчиться неохоче, бо знання даються їй легко;

три – дуже розумна людина, у навчанні не докладає ніяких зусиль;

чотири – людина, якій відкриється істина; гострий розум робить її грубою і жорстокою.

Третій хлопець. Пропоную вам Вічний календар (див. таб.4). За допомогою його ви дізнаєтеся, в який день тижня ви народилися.

Нехай нам потрібно знайти, який день тижня був 14 грудня 2004 року .

Шукаємо в таблиці 4 у стовпцях «роки» 2004 рік; у цьому самому рядку в стовпцях «місяці» в 12 місяці читаємо число 3. Це число додаємо до числа народження, тобто 3+14=17 знаходимо в таблиці «Дні тижня» і дивимося, який це день тижня. Отримали вівторок.

Перший хлопець.. А тепер кожний знайдіть, у який день тижня ви народилися. (Присутні, користуючись таблицею 4 та 1, знаходять дні, у які вони народилися.)

Знайдіть потім за таблицею2 свою планету та ваш метал

Дні тижня Таблиця 1

Неділя	1	8	15	22	29	36
Понеділок	2	9	16	23	30	37
Вівторок	3	10	17	24	31
Середа	4	11	18	25	32
Четвер	5	12	19	26	33
Пятниця	6	13	20	27	34
Субота	7	14	21	28	35

Планета заступниця Таблиця 2

Дні тижня	Планета	Метал
Понеділок	Місяць	Срібло
Вівторок	Марс	Залізо
Середа	Меркурій	Ртуть
Четвер	Юпітер	Олово
Пятниця	Венера	Мідь
Субота	Сатурн	Свинець
Неділя	Сонце	Золото

Третя дівчина. А я відгадаю число, місяць вашого народження і скільки вам років . Порядковий номер вашого місяця народження і скільки вам років. Порятковий номер вашого місяця народження помножте на 100. До добутку додайте число, коли ви народилися. Отриману суму помножте на два. До нового добутку додайте 8. Цю суму помножте на 5. До нового результату додайте 4; суму помножте на 10 і знову додайте 4. Нарешті додайте повну кількість своїх років. Скажіть остаточний результат. Ви народилися….(Ключ для відгадування: від результату відняти 444.Наприклад, названо результат 11697, віднімаємо 444: 1167-444=11253. Дві останні цифри вказують вік (53) роки, попере дві цифри- число народження (12) і попередні цифри- Місяць народження (1). Отже, людина народилася 12 січня їй 53 роки.)

Четвертий хлопець. Я попрошу вийти одного учня. (Виходить бажаючий учень) . Ось тобі дві монети (дає монети номіналом 2к.і 25к.) Я вгадаю, у якій руці яка монета

Числове значення монети, яка у тебе у правій помнож на 4, а числове значення монети, що лежить у лівій руці помнож на 7. Додайте ці числа і скажи: парне чи непарне число ти отримав (Ключ для відгадування: якщо парне число то в правій руці 25к., а в лівій 2 к., якщо непарне, то навпаки).

Четверта дівчина. А я відгадаю номер вашого будинку і скільки вам років. Номер вашого будинку помножте на 50. Тепер додайте кількість своїх років. Додайте 365, відніміть 615. Назвіть результат. Вам… (Ключ для відгадування: нехай вам назвали число 2953. Дві останні цифри вказують на кількість років (53) інші цифри вказують номер будинку (29) . Отже, учаснику 53 роки і номер будинку 29.)

Пята дівчина. Кожній людині при народженні дають імя та прізвище. І вже за ними можна розповісти про їх характер , що передано їй предками через гени, про натуру і спосіб поведінки. Характер визначається за допомогою трьох цифр: інтимної , спадкової та цифри експресії. Інтимна цифра вказує на ті риси і мрії, які кожен приховує від інших; спадкова цифра відкриває те, що кожному передано предками через гени; цифра експресії показує вашу натуру і спосіб поведінки.

Шоста дівчина. Знайдіть свою інтимну цифру за допомогою таблиці 3.

Таблиця 3

А	Б	В	Г	Д	Е	Є	Ж	З
И	Й	К	Л	М	Н	О	П	Р
С	Т	У	Ф	Х	Ц	Ч	Ш	Щ
Ь	І	Ї		Ю	Я
1	2	3	4	5	6	7	8	9

Знайдіть цифри, що відповідають кожній літері вашого імені, додавайте їх до того часу, поки не отримаєте одноцифрове число. ( Наприклад, імені «Тетяна» відповідають цифри 262661, їх сума 2+6+2+6+6+1=23, 2+3=5- інтимна цифра.)

Пояснення до інтимних цифр

Близькі тобі люди вважають, що ти тиран для інших і ненавидиш нерішучих. Ти – особистість імпульсивна, фанатик; або любиш, або ні, чим і керуєшся у своїх вчинках.
Пливеш за течією, підкоряєшся долі. Як особистість – обдарований, цінуєш мистецтво і все прекрасне. Важливу роль для тебе відіграє гармонія почуттів.
Тебе характеризує інтелігентність і рухливість. Використовуєш всі можливості в роботі. Зустрічі, дружні стосунки, подорожі відіграють велику роль у твоєму житті.
Маєш солідну матеріальну базу і докладаєш зусилля для накопичення багатства, грошей - сімї та дому. Життєвим шляхом ідеш упевнено. Ти відмінний працівник, але тобі заважає надмірна обережність, невпевненість у власних силах, надмірна делікатність.
Ти – ентузіаст,намагаєшся бути завжди центрі уваги, не любиш залишатися в тіні. У житті завжди шукаєш свій шанс і намагаєшся його використати, не думаючи особливо про майбутнє. Живеш інтенсивно, не терпиш лежнів і дрібних людей.
Ти дуже реагуєш на оточення. Тобі притаманні спостережливість, працелюбність. Умієш зрозуміти кожного, присвятити себе іншим. Це допомагає тобі удосконалюватися духовно і мати успіх серед оточуючих.
Як особистість ти дружелюбна й енергійна людина –притягуєш інших. У твоєму житті щастя та везіння мають велике значення. Не переносиш інертності. Любиш подорожі і все, що робить життя цікавим , змістовним.
Ти дуже активна людина. Ставиш багато запитань і сам даєш вичерпну відповідь на них. Любиш невідоме, непередбачені проблеми, які тві розум уміє розв’язати.
Умієш безпомилково зрозуміти і розпізнати людину. Швидко пристосовуєшся до оточення. За натурою- ідеаліст. Умієш створювати дистанцію між собою і знайомими. Але одиноким тебе не назвеш. Любиш ділитися радістю з іншими.

Перша дівчина. Спадкова цифра також знаходиться за таблицею 4. На цей раз береться до уваги не імя , а прізвище (у заміжних жінок- дівоче, а людей, які поміняли прізвище-батьківське). Потрібно додати всі цифри, що відповідають літерам прізвища, поки сума не буде одноцифровим числом.

Пояснення до спадкових цифр

Відважно ідеш назустріч будь-якій небезпеці. Як активна людина не любиш перекладати свої справи на інших. Тобі швидко набридає одноманітність і буденність. Намагаєшся змінити таке оточення, реалізувати таке оточення, реалізувати вищі цілі.
Маєш риси, які вважаються вашими сімейними: терпіння, витримка, постійність. Любиш комфорт, красиві речі і і спілкування з людьми.
Тонкий розум, зацікавленість і передбачення допомагають тобі знайти своє місце в житті. Тобі притаманні мрійливість, часом неуважність, але ти вмієш «повертатися з небес на Землю».
Маєш багато позитивних рис, отриманих у спадок від предків.
Найхарактерніші риси –суворість і передбачуваність. Не любиш пустого існування. Служиш своєму оточенню, яке має великий вплив на тві настрій.
Любиш гру, непередбачені ситуації. Умієш подобатися, бути в центрі уваги. Користуєшся увагою дітей. Маєш педагогічний дар.
Любиш мистецтво; нестримана людина, але не любиш виділятися, приховуєш свої почуття, через те дехто вважає тебе імпульсивним, вередливим.
Маєш велику моральну мужність і силу для подолання життєвих труднощів. Людина неспокійної вдачі, певною мірою-фанатик. Тебе однаково притягує і відштовхує матеріальний світ. Завжди готовий до ризику, аби здивувати тих, хто тебе оточує.
Ти альтруїст, ідеаліст, людина широкої душі, можеш пожертвувати ближньому «останню сорочку». Через свою благодійсність станеш мудрим і шанованим.

Друга дівчина Цифра експресії –це сума цифр інтимної і спадкової. Результат суми повинен бути одноцифровим числом.

Пояснення до цифр експресії

Ти амбіційний, упевнений у своїх силах. На цьому тримається твій авторитет. Готуєшся до великих справ, благородних вчинків, але не забуваєш про земну реальність. Любиш керувати, виконувати функції підлеглого для тебе –покарання.
Ти –втіленн я дипломатії. Характер спокійний , ранимий. У твоєму серці порожнеча, яку намагаєшся заповнити коханням. У роботі любиш допомагати іншим (переважно - радити).
Оптиміст, маєш потребу бути в центрі уваги. Обдаровуєш увагою людей неординарних. Активний у роботі, користуєшся успіхом.
Характер-розсудливий і непоступливий, завжди стабільний. Почуття-глибокі . Ти людина слова і діла, любиш працювати. Твої зусилля не зразу, але приведуть до успіху.
Повний енергії, любиш рух, подорожі. Воля –головне твоє багатство. Любиш невеликі . пригоди, легко пристосовушся до нового місця роботи.
У всьому шукаєш гармонії, любиш мистецтво. Душевна рівновага залежить від почуттів. Найвищі цінності – любов, сімя і дім. У роботі береш на себе дуже багато обов’язків.
Повязуєш долю лиш з тими партнерами, які поважають незалежність та оригінальність.
Влада, гроші –самі близькі поняття. Гордість та енергія штовхають тебе на суперництво з іншими. Утверджується в роботі, приймаєш сміливі рішення, добуваєш матеріальні блага. У коханні знаєш, що хочеш, але тобі важко знайти свою долю.
Характер – войовничий , фанатичний. Умієш оцінювати людей. Уважна і вірна людина, алене вагаючись, можеш «спалити мости» і почати все спочатку. Межі між дружбою і коханням не завжди чіткі.

Подруга. Ви побачили, як за допомогою чисел можна дізнатися, що нам доля готує, і багато цікавого про кожну людину.

13 грудня західні та східні християни вважають днем Андрія Первозванного. Хоч Андрій –християнський святий, але народні традиції та обряди цього свята мають стародавній дохристиянський язичеський характер. З давніх-давен в ніч перед Андрієм дівчата ворожать. У ніч на Андрія хлопці мали найбільші права. За всі бешкетування їм люди вибачали

Ніч на Андрія була доленосною. Свято наповнювало буття людини благородним змістом.

Перший хлопець. Що ж, пора і честь знати. Спасибі Вам, паніматінко, за вечорниці.

Господиня. Спасибі і вам, хлопці, дівчата та гості. Заспівайте або заколядуйте мені на прощання. (Дівчата і хлопці співають і з колядкою виходять).

Список використаної літератури

В.І.Кова, С.О. Хмура «Позакласна робота з математики в школах математики»
М.В. Підручна, Г. М. Янченко «Позакласна робота з математики»
Л. Глушенко «Задачі на відсотки» №23(467) 2008р. «Математика» видавництво «Шкільний світ»
М. Тимків «Відсотки. Знаходження відсотків від числа» №18 2008р. «Математика» видавництво «Шкільний світ»
Н. Дерев'янко «Система авторських уроків» №14 (314) 2005р. «Математика» видавництво «Шкільний світ»
Т. Тележникова «Як швидко навчитися рахувати в усно.» 2012р. 4с., 15-19с., 23с., 27,28с.
Л. В. Демчук «Задачі на відсотки» №39 (195) 2002р. «Математика» видавництво «Шкільний світ»
«Позакласна робота» №47-48 (347-348) 2005р. «Математика» видавництво «Шкільний світ»
Дeржaвний стaндaрт бaзoвoї і пoвнoї зaгaльнoї сeрeдньoї oсвіти [Eлeктрoн. рecурc]. – Рeжим дocтупу: https://www.mon.gov.ua/images/files/derzh-standart/post_derzh_stan.doc.

Роки																	Місяці
1801-1900				1901-2000				2001-2099					2101-2188				1	2	3	4	5	6	7	8	9	10	11	12
01	29	57	85		25	53	81		09	37	65	93		05	33	61	4	0	0	3	5	1	3	6	2	4	0	2
02	30	58	86		26	54	82		10	38	66	94		06	34	62	5	1	1	4	6	2	4	0	3	5	0	3
03	31	59	87		27	55	83		11	39	67	95		07	35	63	6	2	2	5	0	3	5	1	4	6	2	4
04	32	60	88		28	56	84		12	40	68	96		08	36	64	0	3	4	0	2	5	0	3	6	1	4	6
05	33	61	89	01	29	57	85		13	41	69	97		09	37	65	2	5	5	1	3	6	1	4	0	2	5	0
06	34	62	90	02	30	58	86		14	42	70	98		10	38	66	3	6	6	2	4	0	2	5	1	3	6	1
07	35	63	91	03	31	59	87		15	43	71	99		11	39	67	4	0	0	3	5	1	3	6	2	4	0	2
08	36	64	92	04	32	60	88		16	44	72			12	40	68	5	1	2	5	0	3	5	1	4	6	2	4
09	37	65	93	05	33	61	89		17	45	73			13	41	69	0	3	3	6	1	4	6	2	5	0	3	5
10	38	66	94	06	34	62	90		18	46	74			14	42	70	1	4	4	0	2	5	0	3	6	1	4	6
11	39	67	95	07	35	63	91		19	47	75			15	43	71	2	5	5	1	3	6	1	4	0	2	5	0
12	40	68	96	08	36	64	92		20	48	76			16	44	72	3	6	0	3	5	1	3	6	2	4	0	2
13	41	69	97	09	37	65	93		21	49	77	00		17	45	73	5	1	1	4	6	2	4	0	3	5	1	3
14	42	70	98	10	38	66	94		22	50	78			18	46	74	6	2	2	5	0	3	5	1	4	6	2	4
15	43	71	99	11	39	67	95		23	51	79			19	47	75	0	3	3	6	1	4	6	2	5	0	3	5
16	44	72		12	40	68	96		24	52	80			20	48	76	1	4	5	1	3	6	1	4	0	2	5	0
17	45	73		13	41	69	97		25	53	81			21	49	77	3	6	6	2	4	0	2	5	1	3	6	1
18	46	74		14	42	70	98		26	54	82			22	50	78	4	0	0	3	5	1	3	6	2	4	0	2
19	47	75		15	43	71	99		27	55	83			23	51	79	5	1	1	4	6	2	4	0	3	5	1	3
20	48	76		16	44	72	00		28	56	84			24	52	80	6	2	3	6	1	4	6	2	5	0	3	5
21	49	77	00	17	45	73		01	29	57	85			25	53	81	1	4	4	0	2	5	0	3	6	1	4	6
22	50	78		18	46	74		02	30	58	86			26	54	82	2	5	5	1	3	6	1	4	0	2	5	0
23	51	79		19	47	75		03	31	59	87			27	55	83	3	6	6	2	4	0	2	5	1	3	6	1
24	52	80		20	48	76		04	32	60	88			28	56	84	4	0	1	4	6	2	4	0	3	5	1	3
25	53	81		21	49	77		05	33	61	89		01	29	57	85	6	2	2	5	0	3	5	1	4	6	2	4
26	54	82		22	50	78		06	34	62	90		02	30	58	86	0	3	3	6	1	4	6	2	5	0	3	5
27	55	83		23	51	79		07	35	63	91		03	31	59	87	1	4	4	0	2	5	0	3	6	1	4	6
28	56	84		24	52	80		08	36	64	92		04	32	60	88	2	5	6	2	4	0	2	5	1	3	6	1

docx

Завантажити

Зберегти на потім

Додав(-ла)

Bilchuk Valentina

Пов’язані теми

Алгебра, 8 клас, Позакласні заходи

Додано

9 січня 2020

Переглядів

1657

Оцінка розробки

Відгуки відсутні

А	Б	В	Г	Д	Е	Є	Ж	З
И	Й	К	Л	М	Н	О	П	Р
С	Т	У	Ф	Х	Ц	Ч	Ш	Щ
Ь	І	Ї		Ю	Я
1	2	3	4	5	6	7	8	9

А	Б	В	Г	Д	Е	Є	Ж	З
И	Й	К	Л	М	Н	О	П	Р
С	Т	У	Ф	Х	Ц	Ч	Ш	Щ
Ь	І	Ї		Ю	Я
1	2	3	4	5	6	7	8	9

А	Б	В	Г	Д	Е	Є	Ж	З
И	Й	К	Л	М	Н	О	П	Р
С	Т	У	Ф	Х	Ц	Ч	Ш	Щ
Ь	І	Ї		Ю	Я
1	2	3	4	5	6	7	8	9