Розробка STEM-уроку. Геометрія. 7 клас

Тема уроку: Геометрія мостів

Мета уроку: узагальнити знання про трикутники; формувати навички та уміння  практичного  використання набутих теоретичних знань, розвивати творчі здібності і логічне мислення учнів при знаходженні ними раціональних шляхів для розв’язування практичних задач; формувати організаційну, соціально-особистісну, інформаційну, життєтворчу компетентності; сформувати уявлення учнів про геометричну фігуру - трикутник, як невід’ємну частину навколишнього нас світу, про значимість даного поняття в соціальному житті людини; показати зв’язок математики із повсякденним життям, зв’язок з іншими науками; сприяти розвитку предметної та життєво необхідної компетентностей; виховувати культуру спілкування; культуру усного мовлення; любов до предмету.

Тип уроку: узагальнення знань.

Вид уроку: змішаний (за проєктною методикою з використанням ІКТ).

Види діяльності: фронтальна, групова, індивідуальна.

Міжпредметні зв’язки: геометрія, інженерія, архітектура, фізика, інформатика, дизайн, історія.

Час проведення: 45 хвилин.

Цільова аудиторія: здобувачі та здобувачки освіти 7 класів.

Обладнання: мультимедійне обладнання, доступ до мережі Інтернет;

Роздатковий матеріал: прямокутник із картону (довжина 28 см, ширина 6 см), пластилін (досить 1-2 частини) та зубочистки, іграшкові дитячі машинки різної ваги (висота і ширина не більше 4 см), ємність для води (довжина 22-26 см), плоскі палиці мінімум 15 (в залежності від того на скільки груп поділено клас).

Інтернет-ресурси:

• генератор створення QR-коду

• відео з YouTube

Хід уроку

I. Організаційний момент

Добрий день, діти. Рада вас бачити на уроці геометрії.

II. Мотивація навчальної діяльності учнів

Трикутник. Чудова геометрична фігура і найпопулярніша в шкільній програмі з геометрії. Багато хто думає, що трикутники «оселилися» тільки на сторінках підручника і більше їх ніде побачити? Чи так це насправді? Чи може людина обійтися без такої геометричної фігури як трикутник? Як часто в житті ми використовуємо трикутні форми? Чи дійсно трикутник одна з основних геометричних фігур? Відповіді на ці запитання ви сьогодні отримаєте на уроці.

План нашого уроку:

1. Теоретична розминка.

2. Практична (дослідницька) робота.

3. Розв’язування практичних задач з життя.

4. Підведення підсумків.

ІІІ. Актуалізація знань. Теоретична розминка

Тож, запрошую до активної роботи. Насамперед, давайте згадаємо деякі поняття з геометрії про трикутники. Будь ласка зіскануйте QR-код та пройдіть невелике теестування. 

2. Практична (дослідницька) робота.

Ну що ж переходимо до практичної роботи. Перед вами лежать прямокутник із кортону (довжина 28 см, ширина 6 см), пластилін (досить 1-2 частини) та зубочистки, іграшкові дитячі машинки різної ваги (висота і ширина не більше 4 см), ємність для води (довжина 22-26 см).

Давайте уявимо, що ємність з водою – це наша річка, і  вам потрібно побудувати такий міцний та стійкий міст, щоб він витримав машинки різної ваги. Якщо ми поставимо лише аркуш картону, то він прогнеться і звичайно ніяка машинка не зможе проїхати, отже треба зробити конструкцію за допомогою зубочисток та пластиліну і таким чином укріпити її та зробити це якомога швидше.

(При побудові конструкцій здобувачі/здобувачки освіти повинні здогадатися, що потрітно для побудови використати форми геометричної фігури трикутник.)

Ваша задача якомога швидше побудувати міцний та стійкий міст за допомогою прямокутника з кортону, пластиліну та зубочисток (або сірників без сірки), щоб по ньому змогли проїхати машинки різної ваги і при цьому конструкція не повинна руйнуватись.

Жорсткість трикутника має велике практичне значення. Особливо під час побудови різних споруд (жорсткість – незмінюваність кутів). Щоб споруди були стійкими, міцними, їх виготовляють так, щоб вони мали якомога більше трикутників в своїй конструкції. 

3. Розв’язування практичних задач з життя.

Діти, пропоную застосувати ваші знання та вміння при розв’язуванні задач.

Задача 1. На малюнку зображено садову хвіртку, яку скоро перекосить. Як прибити планку(дошку), щоб надати міцності хвіртці? Поясніть.

Задача 2. На малюнку показано, як виміряти відстань між пунктами A і B, між якими не можна пройти по прямій. Поясніть вимірювання.

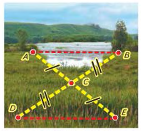
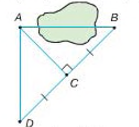
Задача 3. Щоб виміряти на місцевості відстань між пунктами A і B, між якими не можна пройти, виконали таку побудову:  , CD=BC. Тоді шукана відстань AB дорівнюватиме AD. Чому?

4. Підведення підсумків.

Рефлексія. Учні та учениці, ми на початку уроку ставили перед собою мету. Чи досягли ми її? Що нового дізналися? Чи розібралися в даному матеріалі?

Відомий французький архітектор говорив, що освіта – це те, що залишається після того, як все інше забуто. Сподіваюся, все що ви сьогодні почули не забудете та знання, які ви отримали, допоможуть вам на уроках геометрії у старших класах і в житті на практиці, а можливо хтось із вас захоче вибрати професію пов’язану саме з будуванням або архітектурою, дизайном побудов конструкцій. Дякую всім за урок, ви сьогодні добре попрацювали! Відкриваємо щоденники за записуємо домашнє завдання.

Домашнє завдання:

Завдання на кмітливість

Дівчата та хлопці, як ви вважаєте чи можна побудувати такий міст лише із 24 палиць (можна використати і 13), щоб він витримав мінімум 5 підручників.

Міст Да Вінчі

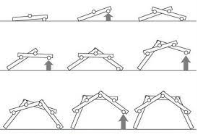
У всьому світі можна знайти різні конструкції мостів. Геометричний дизайн важливий у дизайні мостів. Правильно використані геометричні фігури можуть створити надзвичайно міцні мости. Хоча деякі мости можуть використовувати більше геометричних понять, ніж інші, всі конструкції мостів рівномірно розподіляють вагу для належного підшипника. Трикутники використовуються з боків, а іноді навіть у верхній частині моста. Верхівка мостового мосту може мати конструкцію «х», де чотири трикутники створюють достатню підтримку, щоб нести велику вагу. (Знай більше цікавих фактів про найбільш унікальні мости в світі переглянувши відео.)