Розробка уроку алгебри та початків аналізу для 10 класу

Алгебра та початки аналізу 10 клас

Тема уроку: Застосування похідної до розв'язування прикладних задач.
Мета уроку:
  навчальна: узагальнити, систематизувати і поглибити знання
учнів з теми «Похідна та її застосування», розширити знання учнів про практичне використання похідної, формувати вміння переносити набуті знання в нові ситуації; підготувати учнів до контрольної роботи.
 розвивальна: розвивати вміння аналізувати й узагальнювати вивчений матеріал, увагу, пам’ять, мислення, кмітливість, математичну мову учнів; їх самостійну творчу діяльність.
 виховна: створення комфортних умов для виховання самостійності, взаємоповаги, почуття колективізму, відповідальності, інтересу до предмету.
Обладнання: комп’ютер, інтернет, підручник, роздатковий матеріал.
Тип уроку: узагальнення і систематизація знань.

Хід уроку

І. Організаційний етап
Сьогодні на уроці буде багато висловів відомих людей, хотілося б щоб ви поміркували і користувалися ними.  І починаємо з вислову Конфуція:

«Від того настрою, з яким ви вступаєте в день, або в якусь справу залежать ваші успіхи, а можливо і невдачі»

 Я бажаю вам розпочати урок з гарним настроєм і отримати від нього задоволення і гарні результати.
«Як приємно дізнатися, що ти чогось навчився».
                                          Мольєр.  

«Про свої здібності людина може дізнатися тільки спробувавши їх застосовувати.»

                                                                                        Л.Сенека

 ІІ. Перевірка домашнього завдання

У процесі обговорення домашнього завдання учні повторюють правила диференціювання, алгоритм знаходження найбільшого і найменшого значень функції, знаходження критичних точок.

ІІІ. Основна частина.

1. Онлайн-тести (інтернет)
2. Виступ учня (презентація)
    Найбільший внесок в розвиток диференціального числення внесли Ньютон і Лейбніц. Можливо для вас стануть повчальними факти їхньої біографії.
    Англійський вчений Ісаак Ньютон народився 4 січня 1643 року в родині бідного фермера. Батько помер ще до народження сина. Ісаак був хворою дитиною і ніхто не вірив у те, що він житиме. У 12 років його віддали до найближчої міської школи. Спочатку хлопчик вчився дуже погано і невідомо, як склалася б його доля якби не випадок, що трапився з ним у школі. Один із однолітків побив Ісаака. Від дуже переживав, що це може дати відсіч, бо кривдник був набагато сильнішим. Тоді Ньютон вирішив зробити інакше: перевершити суперника у навчанні. Від досяг своєї мети своєю наполегливою працею. Вчителі визнали його найкращим учнем школи, а згодом Ньютон став геніальним вчителем. У повсякденному житті він дотримувався суворого режиму. Цим він загартовував свій організм і до 80 років був міцним і здоровим.
    Німецький вчений Готфрід Вільгельм Лейбніц народився 1 липня 1646 року в сім’ї професора Лейпцігського університету. Ще до школи малий так захопився читанням, що зовсім покинув дитячі ігри і з ранку до вечора не виходив із бібліотеки. Самотужки вивчив латинську і грецьку мови. В 14 років закінчив школу і вступив до університету. В 16 років отримав ступінь бакалавра, а в 17 – магістра, а у 18 років – став доктором наук.

«Коли починаєш справу, спитай себе:«Що я маю зробити?»,

 після закінчення:«Що я зробив?».
Піфагор.

Учитель: Фундаментом математики служить математичний аналіз. Основою математичного аналізу - взаємопов’язані за змістом розділи – диференціальне та інтегральне числення. Одним із важливих понять математичного аналізу є похідна. І сьогодні, у центрі уваги – застосування похідної до розв’язування прикладних задач.

«Математику вже навіть задля того потрібно вивчати,

що вона розум до ладу приводить»
          М. Ломоносов.

    Сучасні фахівці повинні добре володіти математичним апаратом, який має надзвичайне значення для багатьох професій. Використання теорії диференціального числення є важливим для розвитку сучасної промисловості, економіки, бізнесу, фінансової справи. Тому девізом нашого уроку можуть бути слова:

«Без інтегрального і диференціального числення математика, як наука, не змогла би досягнути свого досконального розвитку»
           Хр. Гюйгенс.

3) Усний рахунок:

1) знайди помилку (вартість питання 1 бал):

а)

б)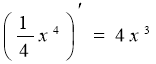

в)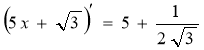   

г)

д)

ж)

4. Щоб ефективно використовувати похідну при розв’язанні конкретних задач, необхідно знати таблицю похідних елементарних функцій. Наступне завдання дасть нам змогу перевірити, як ви вмієте використовувати таблицю похідних. Закодовано прізвище французького вченого, який ввів термін похідна. Скажіть його:

           Учень. Історична довідка (Лагранж).

5. Графічний диктант «Так чи ні?»

«Хоч слова «так» і «ні» короткі, та все ж вами вимагають серйозних роздумів»
           Піфагор

(Учні записують у зошиті відповіді, користуючись символами так ∩, ні −, а потім здійснюють взаємоперевірку за ключем-відповіддю (обмінявшись зошитами)).
 Чи є правильним твердження?
1) Якщо функція неперервна на відрізку [a;b], то вона набуває на цьому відрізку найбільшого і найменшого значення.
2) Якщо функція f(x) не має на відрізку [а;b] критичних точок, то її найбільше і найменше значення будуть досягатися на кінцях відрізка а і b.
3) Якщо між значеннями а і b на відрізку є тільки одна критична точка, і в ній функція досягає максимуму, то можна стверджувати, що цей максимум є найбільшим значенням функції на відрізку [a;b].
4) Якщо функція f(x) має на відрізку [a;b] (в області визначення) максимум, який дорівнює 4, і мінімуми, що дорівнюють -1 і -3, та f(a) = -2; f(b) = 5, то найбільше значення функції на заданому відрізку дорівнюватиме 4.
5) Щоб знайти найбільше і найменше значення функції, слід обчислити значення функції у всіх критичних точках і на кінцях відрізка, а потім з отриманих чисел вибрати найбільше і найменше.
6) Функція може набувати найбільшого і найменшого значення як на кінцях відрізка, так і у внутрішніх його точках.
Ключ-відповідь: 1)∩; 2)∩; 3)∩; 4)−; 5)−; 6)∩;

«Теорія без практики мертва і безплідна, практика без теорії неможлива»
           Рене Декарт
6) Колективне розвязування задачі.

Задача 1. Тіло кинуте вертикально вгору рухається за законом h(t)=6t-t² (h – у метрах, t – у секундах). У який момент часу тіло досягне найбільшої висоти і яке буде її значення в цей момент?
Розв’язання. Знайдемо найбільше значення функції h(t)= 6t-t² для t>0.  h '(t)= 6 – 2t; - 2t + 6=0; t = 3 – критична точка.

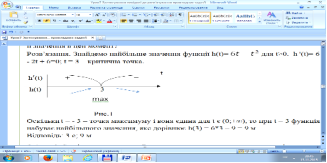Оскільки t = - 3 – точка максимуму і вона єдина для t є (0;+∞), то при t = 3 функція h(t) набуває найбільшого значення, яке дорівнює h(3) = 6х³ – 3² = 9 м.
Відповідь: 3 с; 9 м.

7) Учитель: демонстрація зошита ЗНО з математики та пояснення особливостей складання ЗНО - 2019. Розв’язання завдань з даного зошита по даній темі:

                  9. Укажіть похідну функції  

А                      Б                  В                   Г                  Д

f' (x)=4x³+1      f' (x)=4x³ f' (x)=3x² f' (x)=3x²+1         f' (x)=-2x³+1

 «Добре засвоєна мудрість не забувається ніколи».
       Піфагор.

ІV. 1) Учні відповідають на запитання:
 Чи досягли мети уроку?
 Чи виконали всі завдання уроку?

Застосовуючи прийом «Пінг-понг», учні продовжують фрази:
- Я навчилась…
- Я зрозумів…
- Я закріпила…
- Я повторив…

2) Оцінювання знань учнів (середнє арифметичне, учні самостійно підбивають бали та коментують)

«Корінь навчання гіркий, а плоди його солодкі».
      Аристотель

3) Домашнє завдання

Повторити таблицю похідних елементарних функцій.

Підготувати повідомлення про математиків, які внесли вклад у розвиток поняття похідної(індивідуально).

Завдання №5. Тіло рухається прямолінійно за законом s(t)=t³-2t² (s-вимірюється в метрах, t-у секундах). Знайдіть  швидкість і прискорення цього тіла в момент часу t=1 с.

Підготуватися до контрольної роботи.

 4) Рефлексія
Що сподобалось на уроці?
Що не сподобалося?
Що пропонуєте змінити?
Закінчити урок хотілося б словами:
Дякую за урок. Бажаю всім успіхів.

Таблиця самооцінювання