Розробка уроку алгебри в 8 класі «Розв’язування задач за допомогою квадратних рівнянь»

Розробка уроку алгебри в 8 класі

«Розв’язування задач за допомогою квадратних рівнянь»

Мета:

навчальна: математична компетентність:  сформувати вміння розв’язувати задачі за допомогою квадратних рівнянь;

економічна компетентність: поновити знання про продуктивність праці, ціну товару, відсотки;

розвивальна: пізнавальна компетентність: сприяти розвитку уваги, пізнавальних здібностей учнів; формувати вміння аналізувати, виділяти головне в інформації;

виховна: громадянська компетентність: виховувати старанність, відповідальність, творче ставлення до справи

Тип уроку: засвоєння знань, умінь та навичок

Вид уроку: урок – гра

Обладнання: підручник, картки із завданнями., мультимедійний комплекс

Хід уроку

І. Організаційний етап

   Учитель. Оскільки в наш час дуже важливим є формування життєвих компетентностей учнів та їх економічного мислення, то сьогодні ми з вами уявимо себе економістами будівельної організації і будемо обчислювати продуктивність праці працівників, тобто на уроці математики розв’язуємо  задачі економічного змісту.

ІІ. Актуалізація опорних знань

   Учитель. Те, що рівняння можуть слугувати математичними моделями реальних ситуацій, вам уже відомо з попередніх класів. Тож, давайте пригадаємо послідовність розв’язування задач за допомогою рівнянь (Відповідають учні).

Учитель. Отже, підсумуємо. Розв’язування прикладних задач методом математичного моделювання здійснюється в три етапи:

1. створення математичної моделі задачі;
2. розв’язування відповідної математичної задачі;
3. аналіз відповіді.

ІІІ. Мотивація навчальної діяльності

Учитель.  Мовою математики можна зробити опис будь-якого реального об’єкта чи процесу. Це дає змогу використовувати математику до вирішення багатьох  проблем у будь-якій галузі народного господарства. Історія науки знає багато прикладів, коли в межах вдало побудованої математичної моделі за допомогою обчислень вдавалося передбачити існування нових фізичних явищ та об’єктів. Метод математичного моделювання відіграє велику роль у корабле- та авіабудуванні, економіці тощо.

 Отож, без належної математичної підготовки неможлива  повноцінна освіта сучасної людини.

ІV. Вивчення нового матеріалу.

Учитель.   У 7 класі ми з вами навчилися розв’язувати задачі за допомогою лінійних рівнянь. Але математичною моделлю багатьох  задач у математиці, фізиці, техніці, практичній діяльності людини  може бути не тільки лінійне рівняння чи система лінійних рівнянь, а й квадратне рівняння.

Уявляємо ситуацію: керівник будівельної організації вирішив перевірити доцільність кількості працівників, які працюють на його підприємстві. Для цього йому необхідно вивчити і проаналізувати стан продуктивності праці працівників. Оскільки ми сьогодні з вами 45 хвилин працюємо в економічному відділі цієї організації, то нам необхідно обчислити показники продуктивності праці на різних ділянках діяльності підприємства. Отож, розглянемо задачу.

Задача. Відомо, що один з мулярів затрачає на виконання деякої кладки на 5 год. більше, ніж другий. Знайдіть час, який потрібний кожному муляру окремо для здійснення цієї кладки, якщо обидва муляри, працюючи разом, можуть її зробити за 6 год. (Виконують учні, учитель лише спрямовує правильність розв’язку).

Розв’язання.  Припустимо, що вся робота мулярів дорівнює 1. Нехай другому муляру для здійснення кладки необхідно х год., тоді першому – (х + 5) год. За 1 годину  другий  муляр виконає частини кладки,  а  перший – частини кладки. За умовою задачі відомо, що якщо обидва муляри працюють разом, то їм необхідно 6 год. для виконання усієї кладки. Отже, маємо рівняння:  (+) 6 = 1

                              +– 1 = 0

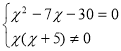
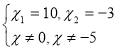
Оскільки другий корінь рівняння менший від нуля, то він не задовольняє умову задачі, отже другому муляру для здійснення кладки необхідно 10 год., тоді першому муляру необхідно 10 + 5 = 15 годин.

Відповідь: 1 муляр – 15 год., 2 муляр – 10 год.

   Учитель. Після виконання даної задачі, давайте спробуємо пригадати  і сформулювати означення економічного терміну «продуктивність праці» (Відповіді учнів).

Продуктивність праці - це обсяг роботи, що може бути виконана за одиницю часу.

V. Засвоєння нових знань і вмінь

   Учитель Отож, сьогодні ми маємо надати керівнику підприємства всі необхідні дані для здійснення аналізу стану продуктивності праці на даному підприємстві. Для цього розглянемо ряд задач на визначення продуктивності праці працівників.

Задача 1. Одна бригада працювала на ремонті дороги 7 год., після чого до неї приєдналася друга бригада. Через 2 год. спільної роботи ремонт було закінчено. За скільки годин може відремонтувати дорогу кожна бригада, працюючи самостійно, якщо першій для цього потрібно на 4 год. більше, ніж другій?

Розв’язання. Нехай перша бригада може самостійно відремонтувати дорогу за х год., тоді другій для цього потрібно (х – 4) год. За 1 год. перша бригада ремонтує частину дороги,  а друга – частину дороги. Перша бригада працювала 9 год. і відремонтувала   частину дороги, а друга працювала 2 год. і відремонтувала відповідно дороги. Оскільки в результаті було відремонтовано всю дорогу, то маємо рівняння:

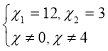
х = 3 не задовольняє умову задачі, оскільки тоді друга бригада мала б відремонтувати дорогу за 3 – 4 = -1 (год.), що не має змісту.

  Отже, перша бригада може відремонтувати дорогу за 12 год.. а друга – за 8 год.

Відповідь: 12 год., 8 год.

Задача 2. Дві бригади, працюючи разом, виконують деяку роботу за 3 год. 36 хв., а працюючи окремо, половину цієї самої роботи перша бригада виконує на 1,5 год. швидше, ніж друга. За який час може виконати цю роботу кожна бригада, працюючи окремо?

Розв’язання. Приймемо всю роботу за 1.  Нехай перша бригада виконає роботу за х год., тоді другій бригаді для виконання цієї роботи знадобиться (х+ 3) год. За 1 год. перша виконає частину роботи, а друга – частину роботи. Працюючи разом за 3 год., 36 хв. вони виконають усю роботу ( 3 год. 36 хв. = год. = год. = год) за год.  Маємо рівняння:

/5

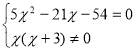
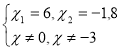
Оскільки другий корінь рівняння менший від нуля, то він не задовольняє умову задачі, отже перша бригада виконає роботу за 6  год., а друга бригада за 6 + 3 = 9 годин.

 Відповідь: 6 год., 9 год.

Задача 3. Один робітник може виконати певну роботу на 24 год. швидше, ніж другий. Працюючи разом, вони виконують її за 35 год. скільки часу потрібно кожному з робітників, щоб виконати певну роботу, працюючи самостійно?

Розв’язання.  Усю роботу приймемо за 1. Нехай перший робітник виконує її за х год., тоді другий – за (х + 24) год. Продуктивність праці першого частини роботи, другого частини роботи. Разом усю роботу вони виконують за 35 год. Маємо рівняння:

( + ) 35 = 1

+ – 1 = 0

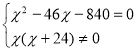
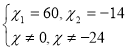
Оскільки другий корінь рівняння менший від нуля, то він не задовольняє умову задачі, отже перший робітник виконає роботу за 60  год., а другий  за

 60 + 24 = 84 години.

Відповідь: 60 год., 84 год.

VІ. Підсумки уроку

Учитель. Ми сьогодні виконували роль економістів будівельної організації і надавали керівнику інформацію про стан продуктивності праці на підприємстві. При виконанні завдань всі працювали відповідально, тому що саме на основі цієї інформації керівник буде приймати рішення про доцільність кількості працівників, які працюють на підприємстві.

     А тепер я б хотіла, щоб ви висловили свої враження про урок  ( відповіді учнів).

VІІ. Домашнє завдання

Завдання за підручником  §  26,   № 983, 985.