Розробка уроку на тему "Чотирикутники."
Урок № 1
Тема. Чотирикутники
Мета: сформувати уявлення про чотирикутник, його елементи: вершина, сторона, діагональ, сусідні сторони (вершини), протилежні сторони (вершини); ввести поняття периметра чотирикутника. Сформувати первинні вміння:
- відтворювати означення чотирикутника, його елементів;
- знаходити на рисунку зображення чотирикутника та його елементів;
- виконувати рисунки за описом;
- розв'язувати найпростіші задачі на обчислення із використанням поняття периметра чотирикутника.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Чотирикутники».
Хід уроку
I. Організаційний етап
Вступне слово вчителя про:
- особливості вивчення геометрії у 8 класі;
- організацію навчального процесу у 8 класі;
- будову підручника.
II. Перевірка домашнього завдання
Вчитель перевіряє літнє домашнє завдання (якщо таке було задано).
ІІІ. Формулювання мети і завдань уроку
Усвідомленому сприйняттю учнями матеріалу уроку може сприяти робота з повторення та усвідомлення найважливіших понять, вивчених у 7 класі (цю роботу проводимо на етапі актуалізації знань та вмінь учнів), зокрема формується думка про те, що серед найважливіших понять курсу геометрії 7 класу можна виділити трикутник. Необхідно звернути увагу учнів на систему вивчення геометричної фігури «трикутник»: означення → елементи → властивості → поняття рівності → ознаки рівності → розв'язування задач із використанням теоретичних відомостей про трикутник.
Після проведеної роботи з повторення означення та основних властивостей трикутника пропонуємо учням виконати завдання.
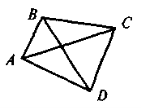
На площині дано 4 точки; розгляньте всі можливі випадки їх взаємного розташування. Які фігури утворяться, якщо поєднати всі можливі випадки їх взаємного розташування? Які можливі варіанти взаємного розташування 4-х точок та фігур, що утворяться в результаті послідовного з'єднання точок відрізками.
Зосереджуємо увагу учнів на випадку, коли жодні три точки не лежать на одній прямій і жодні два відрізки не мають спільних внутрішніх точок, та таким чином формулюємо основну дидактичну мету уроку — вивчити згаданий випадок та його найпростіші властивості.
IV. Актуалізація опорних знань
Виконання усних вправ
- Чи правильні наведені твердження?
1) Через точку площини можна провести не менш ніж 1000 прямих;
2) сполучивши попарно три точки на площині, завжди дістанемо три прямі;
3) на кожній прямій можна вибрати принаймні 100 точок.
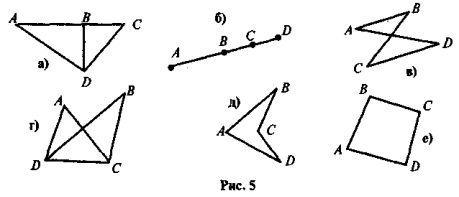
- Скільки трикутників зображено на рисунку 1? Назвіть їх.
- Скільки трикутників зображено на рисунку 2? Назвіть їх.
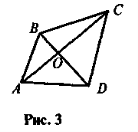
- Знайдіть усі трикутники (рис. 3), дві вершини яких знаходяться в точках А та В.
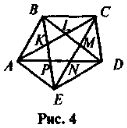
- Знайдіть усі трикутники (рис. 4), дві вершини яких знаходяться в точках А та В.
V. Засвоєння знань
План вивчення нового матеріалу
- Означення чотирикутника.
- Елементи чотирикутника.
- Периметр чотирикутника.
Означення чотирикутника є одним із найважливіших означень курсу геометрії 8 класу. Саме тому усвідомленому сприйняттю цього означення допоможе робота, проведена на етапі формулювання мети уроку: учні мають зрозуміти, що для існування чотирикутника з вершинами в даних чотирьох точках необхідне одночасне виконання двох умов:
- жодні три з даних чотирьох точок не повинні лежати на одній прямій;
- жодні дві сторони (відрізки, що з'єднують ці точки) не повинні мати точок перетину (внутрішніх).
Завдання. Чи є чотирикутником фігура, утворена точками А, В, С і D та відрізками АВ, ВС, CD і AD?
Під час вивчення питання про елементи чотирикутника корисно було б зробити порівняння з елементами трикутника (дослідити, як впливає збільшення кількості вершин многокутника на його елементи). Тоді зрозуміло, що, на відміну від сторін та кутів трикутника, сторони і куги чотирикутника можуть бути по-різному розташовані один відносно іншого (таким чином, вводиться поняття протилежних, сусідніх, суміжних сторін або вершин чотирикутника). Також важливим є питання про правильне позначення чотирикутника (у цьому питанні учні часто припускаються помилок): важливо, щоб учнів усвідомили, що, на відміну від позначення трикутника (усі вершини якого називають у довільному порядку), позначаючи чотирикутник, його вершини треба називати тільки послідовно (букви, що стоять поряд у позначенні чотирикутника, визначають сусідні вершини або одну із сторін чотирикутника). Усвідомленому сприйняттю цього фрагменту матеріалу допоможе робота за готовими рисунками.
Завдання. Чи можна чотирикутники, що зображені на рисунку 6, позначити MNKP?

Порівнюючи трикутник і чотирикутник, можна сформувати поняття діагоналі чотирикутника (для усвідомлення учнями змісту цього поняття можна запропонувати питання про неможливість існування діагоналі трикутника) та периметра чотирикутника.
Під час засвоєння нових знань доцільно складати з допомогою учнів опорний конспект, в якому теоретичні відомості подані в стислому вигляді.
|
Конспект 1 |
||
|
Чотирикутники |
||
|
1. ABCD — чотирикутник. а) точки А, В, С і D — вершини, причому А і В — сусідні; А і С — протилежні; б) відрізки АВ, ВС, CD і AD — сторони, причому: АВ і AD — сусідні, АВ і CD — протилежні; в) відрізки АС і BD — діагоналі. |
|
|
|
2. Для чотирикутника ABCD сума АВ + BC + CD+ AD — периметр; P = AB + BC + CD + BD |
||
|
3.
|
||
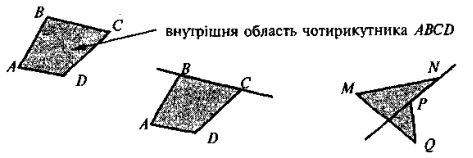
|
ABCD — опуклий чотирикутник; MNPQ — неопуклий чотирикутник. |
||
|
4. Якщо ABCD — опуклий чотирикутник, то:
|
|
|
VI. Формування первинних умінь
Виконання усних вправ
- Скільки сусідніх вершин має вершина чотирикутника? Скільки протилежних? Назвіть сусідні й протилежні вершини для вершини В чотирикутника ABCD.
- Скільки сусідніх сторін має сторона чотирикутника? Скільки протилежних? Назвіть сусідні й протилежні сторони для сторони AD чотирикутника ABCD.
- Відрізок, який сполучає дві вершини чотирикутника, не є його діагоналлю. Чи можуть дані вершини бути протилежними?
- Вершинами чотирикутника є точки К, L, М, N.
а) Відомо, що KM і ML — сторони чотирикутника. Назвіть його діагоналі.
б) Відомо, що KL — діагональ чотирикутника. Назвіть вершини, сусідні з вершиною К.
в) Даний чотирикутник можна назвати KMLN. Чи можна його назвати MLAN?
Виконання графічних вправ
Позначте точки А, В, С і D, які не лежать на одній прямій, і послідовно сполучіть їх відрізками так, щоб утворився чотирикутник. Дайте назву здобутому чотирикутнику і проведіть його діагоналі.
Виконання письмових вправ
- Знайдіть периметр чотирикутника, якщо його найменша сторона дорівнює 5 см, а кожна наступна сторона на 2 см більша за попередню.
- Знайдіть сторони чотирикутника, якщо його периметр дорівнює 3 дм, а одна сторона менша від кожної з трьох інших на 2 см, 3 см і 5 см відповідно.
3*. Периметр чотирикутника ABCD дорівнює 23 дм. Знайдіть довжину діагоналі АС, якщо периметр трикутника ABC дорівнює 15 дм, а периметр трикутника ADC дорівнює 22 дм.
 VII. Підсумки уроку
VII. Підсумки уроку
Тестове завдання
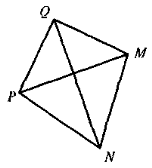
Яке з тверджень неправильне? У чотирикутнику PQMN (див. рис):
- вершини М і N сусідні з вершиною Q;
- вершина N протилежна вершині Q;
- відрізки QN і РМ — діагоналі;
- NP і NM — сусідні сторони.
VIII. Домашнє завдання
Вивчити зміст основних понять уроку. Розв'язати задачі.
- Чи існує чотирикутник ABCD, в якому АВ = 9 см, ВС = 12 см, АС = 21 см? Відповідь обґрунтуйте.
- Периметр чотирикутника дорівнює 20 см. Знайдіть сторони чотирикутника, якщо одна з них складає 40 % периметра, а три інші рівні.
-
 Сторони чотирикутника відносяться як 3 : 4 : 5 : 6. Знайдіть периметр чотирикутника, якщо сума його найбільшої і найменшої сторін дорівнює 18 см.
Сторони чотирикутника відносяться як 3 : 4 : 5 : 6. Знайдіть периметр чотирикутника, якщо сума його найбільшої і найменшої сторін дорівнює 18 см.
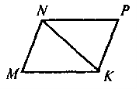
- (На повторення). Відомо, що AKMN=ANPK (див. рис).
а) Доведіть, що MK || NP;
б) знайдіть ![]() P, якщо
P, якщо ![]() M = 65°.
M = 65°.


про публікацію авторської розробки
Додати розробку