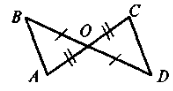розробка уроку на тему "Властивості паралелограма"
Урок № 5
Тема. Властивості паралелограма
Мета: доповнити знання учнів властивостями бісектрис кутів паралелограма та висот паралелограма; продовжити роботу із формування вмінь відтворювати вивчені означення і властивості паралелограма та використовувати ці твердження під час розв'язування задач на обчислення і доведення.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: конспект «Паралелограм».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Для перевірки якості засвоєння учнями основних понять уроку можна провести математичний диктант.
Математичний диктант
Варіант 1
- Чотирикутник КЕРМ — паралелограм. Скільки спільних точок мають прямі КЕ і РМ ?
- Діагоналі паралелограма дорівнюють 7 дм і 5 дм. На відрізки якої довжини вони діляться точкою перетину?
- Один із кутів паралелограма дорівнює 35°. Чому дорівнюють решта його кутів?
- Периметр паралелограма дорівнює 20 см, а одна з його сторін — 3 см. Знайдіть довжини інших його сторін.
Варіант 2
- Чотирикутник ВСОЕ — паралелограм. Чи може кожний із кутів В і Е дорівнювати 80°?
- С — точка перетину діагоналей паралелограма ОВКМ, Чому дорівнюють його діагоналі, якщо довжини відрізків CO і СВ дорівнюють 3,5 см та 2,5 см відповідно?
- Периметр паралелограма дорівнює 26 см, а одна із його сторін — 5 см. Знайдіть довжини решти сторін.
- Один із кутів паралелограма дорівнює 45°. Чому дорівнюють решта Його кутів?
Правильність розв'язання задач домашньої роботи перевіряємо після виконання і перевірки математичного диктанту.
III. Формулювання мети і завдань уроку
З метою створення мотивації діяльності учнів та усвідомленого розуміння ними важливості матеріалу, що виноситься на урок, можна запропонувати виконати завдання.
Виконайте зображення паралелограма ABCD з гострим кутом ![]() A = 60° та проведіть у ньому:
A = 60° та проведіть у ньому:
- бісектрису АК (точка К належить стороні ВС) кута А; знайдіть на рисунку всі рівні кути; визначте вид трикутника АВК;
- бісектрису ВМ кута В; позначте точку L — точку перетину бісектрис; визначте вид трикутника ABL;
- бісектрису CN кута С паралелограма; визначте взаємне розташування прямих АК і CN;
- висоти ВК і BF. Яку градусну міру має кут HBF ?
Після виконання завдань формулюється питання про існування властивостей інших елементів паралелограма (окрім сторін, кутів та діагоналей). Відповідь на сформульоване таким чином запитання складатиме основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь
З метою свідомого розуміння та подальшого засвоєння учнями змісту властивостей бісектрис та висот паралелограма слід активізувати знання і вміння учнів: означення бісектриси кута, ознаки рівнобедреного трикутника, властивості сусідніх та протилежних кутів паралелограма, ознак паралельності двох прямих, що перетнуті третьою, ознаки та властивості кутів прямокутного трикутника.
Для виконання цієї задачі учні розв'язують усні вправи.
Виконання усних вправ
- Вправи за готовими рисунками.
|
1. |
|
Дано: АО = ОС,ОВ = OD. Довести: AB || CD |
|
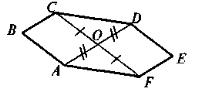
2. |
|
Дано: АО = OD, CO = OF. Довести: CD || AF |
|
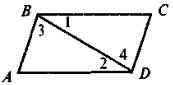
3. |
|
Дано: Довести: АВ || СD, ВС || AD |
|
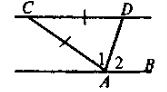
4. |
|
Дано: AC = CD, Довести: AB || CD |
|
5 |
|
Дано: Довести: ΔABC — рівнобедрений |
- Сума кутів паралелограма дорівнює 100°. Чому дорівнює кожний із цих кутів?
- Відомо, що коли в трикутнику один кут прямий, то два інші — гострі. А чи правильне обернене твердження?
V. Засвоєння знань
План вивчення нового матеріалу
- Властивість бісектриси кута паралелограма.
- Властивість бісектрис сусідніх кутів паралелограма.
- Властивість бісектрис протилежних кутів паралелограма.
- Властивість відрізка з кінцями на паралельних сторонах паралелограма, що проходить через точку перетину діагоналей паралелограма.
5*. Властивість висот паралелограма, що проведені із:
- вершин гострого кута паралелограма;
- вершин тупого кута паралелограма.
Оскільки навчальний матеріал уроку не є обов'язковим для вивчення, тому його можна подати, розв'язуючи опорні задачі. Але автор вважає за доцільне розглянути з учнями названі властивості, бо вони мають досить широке застосування під час розв'язування геометричних задач. Доведення вищезазначених опорних фактів можна здійснювати під час розв'язування задач або як узагальнення спостережень, здійснених на етапі формулювання мети (коли було розглянуто конкретний паралелограм), використовуючи при цьому окремі знання з курсу геометрії 7 класу (див. Актуалізація...). Якщо рівень пізнавальної активності учнів є досить низьким, учитель може принаймні сформулювати названі властивості та запропонувати їх для доведення тільки сильним учням в якості індивідуального домашнього завдання (яке потім оцінити).
У будь-якому разі повний перелік властивостей елементів паралелограма міститься в конспекті «Паралелограм».
VI. Застосування знань, умінь та навичок
Виконання усних вправ
- Висоти паралелограма, що виходять з вершини тупого кута, утворюють кут 40°. Знайдіть кути паралелограма.
- Відрізок, що проходить через точку перетину діагоналей паралелограма, кінці якого належать сторонам паралелограма, дорівнює 5 см. На які відрізки ділиться цей відрізок точкою перетину діагоналей?
-
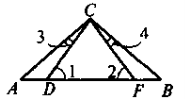
 Під яким кутом перетинаються бісектриси кутів паралелограма, що виходять із двох суміжних вершин паралелограма?
Під яким кутом перетинаються бісектриси кутів паралелограма, що виходять із двох суміжних вершин паралелограма?
-
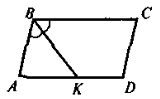
У паралелограмі
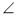 ABK =
ABK =  CBK = 60°
CBK = 60°
(див. рис). РАВК = 12. Знайдіть ВК.
Виконання письмових вправ
- Периметр паралелограма ABCD дорівнює 14 дм, а периметр трикутника ABC — 10 дм. Знайдіть довжину діагоналі АС.
- Знайдіть кути паралелограма, якщо:
а) бісектриса його кута перетинає сторону під кутом 35°;
б) висота паралелограма утворює з однією з його сторін кут 42°.
- Бісектриса кута D паралелограма ABCD ділить сторону ВС у відношенні 1 : 4, починаючи від точки В. Знайдіть периметр паралелограма, якщо ВС = 15 см.
- У паралелограмі ABCD АВ = 7 см, AD = 12 см. Бісектриса кута А перетинає сторону ВС у точці К. Знайдіть довжину відрізків ВК і КС.
5*. Знайдіть кути паралелограма, якщо його діагональ перпендикулярна до однієї зі сторін і дорівнює половині іншої сторони.
6* (опорна). Кут між висотами паралелограма, проведеним з однієї вершини, дорівнює куту паралелограма при сусідній вершині. Доведіть.
VII. Підсумки уроку
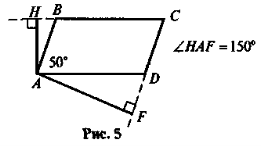
Чи існують паралелограми, що зображені на рисунках 1-5?
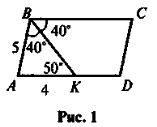
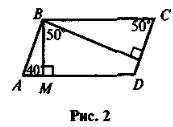
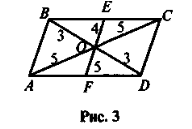
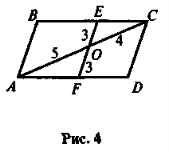
VIII. Домашнє завдання
Вивчити зміст властивостей бісектрис і висот паралелограма. Розв'язати задачі.
- Сума трьох сторін паралелограма дорівнює 15 м, сума трьох інших його сторін —18 м. Знайдіть периметр паралелограма.
- Знайдіть кути паралелограма, якщо:
а) бісектриса його кута перетинає сторону під кутом 25°;
б) висота паралелограма, проведена з вершини тупого кута, ділить його у відношенні 1:3.
3*. Бісектриса кута паралелограма ділить його сторону на відрізки завдовжки 5 см і 6 см. Знайдіть периметр паралелограма. Скільки розв'язків має задача?
4* (на повторення). У чотирикутнику ABCD AB = CD. Яке співвідношення необхідно додати до умови, щоб за даними задачі довести, що чотирикутник ABCD — паралелограм? Висловіть припущення.


про публікацію авторської розробки
Додати розробку