Розробка уроку на тему "Квадрат двочлена"

Тема. Квадрат двочлена

Мета: домогтися свідомого розуміння учнями змісту формул «квадрат суми» та «квадрат різниці двох виразів»; виробити первинні вміння засто­совувати ці формули для перетворення квадрата двочлена у многочлен стандартного вигляду.

Тип уроку: засвоєння знань.

Хід уроку

І. Аналіз тематичної контрольної роботи

 Навчального часу обмаль, тому, якщо врахувати, що учні провели самоперевірку завдань (див. попередній урок), самоактуалізацію знань та виконали попередню роботу вдома, можна зібрати зошити і врахувати її як допуск до корекції знань та вмінь (якщо така робота запланована вчителем).

Якщо ж проводимо корекційну роботу, вчитель приділяє на цьому уроці   5-10 хвилин навчального часу на пояснення розв'язання найсклад­ніших задач.

II. Актуалізація опорних знань

1. Подайте у вигляді добутку: а²; (2а)²; (а + b)²; (а – b)²; (2а – b)².
2. Знайдіть добуток: (2а)b; 2а(а + b); (а + b)(а + b); (а – b)(а – b).
3. Прочитайте словами вирази (використовуючи поняття «сума», «різ­ниця», «квадрат», «добуток» і т. д.):

(а + 5)²; а² + 5²; а² – 5²; (а – 5)²; а² – 2аb + b²; а та -а; а² та (-а)²; а² та -а².

4. Порівняйте: а + b та –a – b; (a + b)² та (-а – b)²; (а + b)² та -(а + b)².

III. Робота з випереджальним домашнім завдання

 Оскільки пропедевтичні вправи для виконання 1-ї частини випе­реджального домашнього завдання були опановані раніше (див. 2-й урок теми «Множення многочлена на многочлен»), то всі учні повинні впоратися із цим завданням, а саме: дістати записи вигляду:

та  ,

де Δ та О — дані одночлени — члени двочленів, що їх підносять до квадрата.

Якщо учні виконали порівняння за алгоритмом, то залишиться тільки узагальнити результати спостережень та сформулювати відповідну формулу.

IV. Засвоєння знань

 Для формування знань формул квадрата двочлена ми використову­вали індуктивний метод, тобто від конкретних прикладів, в яких учні легко виконують перетворення згідно з логічним ланцюжком: квадрат перетворити в добуток → добуток у суму → суму в много­член стандартного вигляду, переходимо до загального правила, яке показує, як перейти від першої ланки сформованого ланцюжка од­разу до останньої (тобто раціоналізувати перетворення).

На цьому етапі присутній мотиваційний момент (бо часто учні не усвідомлюють, навіщо вивчати формули, якщо для їх виведення застосо­вується алгоритм множення многочленів та й традиційне поняття «виве­сти формулу» зрозуміле далеко не кожному).

На цьому етапі переходу від конкретного до загального дуже важливо, щоб: 1) учні усвідомили, що букви а і b в традиційному записі є умовними,  тобто за домовленістю означають лише якісь два різні вирази; 2) а з п. 1) дуже важливо вміти відтворювати формули не тільки для а та b, а й для будь-яких двох виразів, а цьому сприяє словесне формулювання цих формул.

Тому запис формул та прикладів у зошити може мати такий вигляд:

Одразу слід наголосити, що формули (а ± b)² не є окремими, не зв'язаними між собою — навпаки, це два прояви однієї формули квадрата двочлена й відрізняються лише знаком подвоєного добутку.

V. Засвоєння вмінь

 На перших етапах закріплення навичок застосування формул

(a ± b)² = a² ± 2ab + b²

слід виконувати вправи, що спрямовані на відпрацювання цих навичок, що базуються на безпосередньому відтворенні формул, а потім виразів, пов'язаних із нескладними пе­ретвореннями.

Виконання усних вправ

1. Прочитайте рівності. Чи є вони тотожностями? Чому?

1) (х + у)² = х² + у²; 2) (х + у)² = х² + 2ху + у²; 3)(х – у)² = х² – у²;

4) (х – у)² = х² – 2ху + у²; 5) (2х – у)² = 2х² – 2ху + у²;

6) (2х – у)² = (2х)² – 2 ∙ 2х ∙ у + у².

2. Піднесіть до квадрата двочлен:

1) а + 2; 2) а – 2;  3) а – 3;  4) а + 3;  5) у – 7;  6) 7 + у.

Виконання письмових вправ

1. Перетворіть у многочлен:

1) (р – q)²; 2) (b + 3)²; 3)(у – 9)²; 4) (а + 12)²; 5) (15 – х)²; 6) (z – 11)².

2. Подайте вираз у вигляді суми:

1) (а + 2)²; 2) (6 – х)²; 3) (3х – 4)²; 4) (5т + 3п)²; 5) (0,1а + 10b)²;

6) 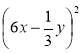; 7) (п² + 1)²; 8) (х⁴ – x²)²; 9) (у⁴ + у³)²; 10) ;

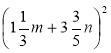11) (6ab² – а²b)²; 12) (5а⁴ – 2а²b⁴)².

 Слід одразу попередити помилки, які традиційно допускають семикласники у випадку, коли один з членів двочлена, що підноситься
до другого степеня, є добутком (див усні вправи).

3. Спростіть вираз:

1) (х – 3)² – 9; 2) 12х – (х – 6)² ; 3) (2a – 3b)² – (3а + 2b)²;

4) (2х – 3у)² + (4х + 2у)²; 5) (х – 5)² – х(х + 3); 6) (6а – b)² + (9a – b)(4a + 2b).

VI. Підсумки уроку

Допишіть замість (*) такі вирази, щоб рівності стали правильними:

(т(*)п)² = т² + 2т* + (*);   (т – п)* = (*)² (*) 2тп * п².

VII. Домашнє завдання

№ 1. Використовуючи формули «квадрат двочлена», перетворіть у су­му вирази:

1) (х + 3)²; 2) (4 – у)²; 3) (2т – 5)²; 4) (7а + 6b)²; 5) (0,2х – 10у)²;

6) 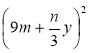; 7) (а² – 1)²; 8)(х³ + 3х²)²; 9) (х + 4)² – 16; 10) 10а – (а – 5)²;

11) (3т – 7п)² – (3т + 7п)²; 12) b(b + 3) – (b – 4)².

№ 2. 1) Піднесіть до квадрата вирази: (х – 1); (х + 1); (а + 3)(а – 3).

2) Замініть вирази на протилежні. Як це зробити? Запишіть утворені ви­рази у вигляді суми та піднесіть до квадрата за формулою «квадрат суми двох виразів». Спростіть утворені многочлени та порівняйте їх із много­членами, здобутими в попередньому пункті.