Розробка уроку на тему "Мішані числа."
Тема. Мішані числа.
Мета: вдосконалити знання і вміння.
Тип уроку: комбінований.
Хід уроку
І. Перевірка домашнього завдання
Розв'язання домашніх вправ можна перевірити так:
№751(5, 7, 8, 9, 10) записати заздалегідь за дошкою, на уроці звірити відповіді;
№756, 754(1, 2) біля дошки розв'язують три учні;
№740(1) — перший учень біля дошки виконує розв'язання задачі.
Під час підготовки до відповідей учнів, що працюють біля дошки, основна частина класу розв'язує кодовані вправи (за змістом близькі до №751).
Обчислити значення:
|
І |
II |
|
1) 6 + |
1) |
|
2) а – 1 |
2) а – 3 |
|
3) 6 + 7 |
3) 6 + 10 |
|
4) с – 3 |
4) с – 2 |
Кодовані відповіді:
1) 7![]() ; 2) 6
; 2) 6![]() ; 3) 5
; 3) 5![]() ; 4) 13; 5) 1
; 4) 13; 5) 1![]() ; 6) 5
; 6) 5![]() ; 7) 4
; 7) 4![]() ; 8) 12.
; 8) 12.
Зміст кодованих вправ полягає в тому, що учень, виконавши першу вправу, шукає отриману відповідь серед наданих кодованих відповідей. Якщо відповіді, яку отримав учень, немає серед кодованих, то учень припустився помилки. Виконавши всі завдання свого варіанта, учень подає вчителю роботу з кодованою відповіддю. Наприклад, 4321, що означає:
а = 13, b = 5![]() , с = 6
, с = 6![]() , d = 7
, d = 7![]() .
.
Таких завдань можна приготувати стільки, щоб забезпечити роботою кожного учня і виключити списування.
II. Повторення та узагальнення знань
Під час перевірки домашнього завдання і кодованих вправ учні повторюють основні означення (мішані числа, правильні дроби), правила та алгоритми розв'язування вправ (перетворення неправильного дробу у мішане число і навпаки).
Для більш ясного розуміння змісту теми учням треба відповісти на узагальнюючі запитання вчителя:
- Наведіть приклад:
- правильного дробу;
- неправильного дробу, що дорівнює 1.
- неправильного дробу, що більший за 1.
Поясніть, чому ви так вважаєте.
- Наведіть приклад мішаного числа. Чому воно так називається?
-
Поясніть, як:
-
число
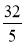 подати у вигляді мішаного числа;
подати у вигляді мішаного числа;
-
мішане число 3
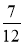 подати у вигляді неправильного дробу;
подати у вигляді неправильного дробу;
-
додати: 6 +
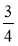 ; 6 + 1
; 6 + 1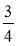 ; 6
; 6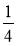 + 6
+ 6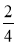 ; 6
; 6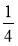 + 1
+ 1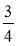 ; 6
; 6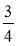 + 2
+ 2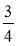 ;
;
-
відняти: 5
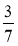 – 2
– 2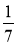 ; 5
; 5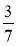 – 2
– 2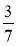 ; 1 –
; 1 – 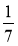 ; 5 –
; 5 – 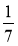 ; 5 – 2
; 5 – 2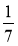 ; 5
; 5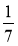 – 2
– 2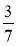 .
.
-
число
III. Вдосконалення знань
На цьому уроці учні розв'язують вправи достатнього та підвищеного рівня на всі дії з дробовими числами (включаючи перетворення правильних дробів та мішаних чисел): №№ 763, 765.
Додаткові задачі
-
За перший день турист пройшов
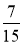 маршруту, а за другий — решту 24км. Знайдіть довжину всього маршруту.
маршруту, а за другий — решту 24км. Знайдіть довжину всього маршруту.
-
У шкільну їдальню привезли апельсини, мандарини і банани. Апель
сини становили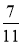 всіх фруктів, мандарини —
всіх фруктів, мандарини — 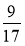 остачі, а банани — решту 32 кг. Скільки всього кілограмів фруктів завезли в їдальню?
остачі, а банани — решту 32 кг. Скільки всього кілограмів фруктів завезли в їдальню?
- Розв'яжіть рівняння:
 1)
1) ![]() ; 2)
; 2) 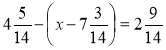 .
.
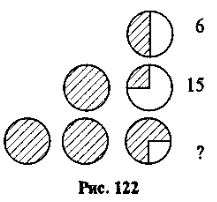
- Знайдіть пропущене число (рис. 122).
Розв'язання вправ (коментарії і відповіді)
№ 763. Вправа допомагає повторити правила порівняння дробів:
1) з однаковими знаменниками;
2) з однаковими чисельниками, а також правила читання і зміст подвійних нерівностей.
1) 2![]() =
= ![]() ; 3
; 3![]() =
= ![]() , тому
, тому ![]() <
< ![]() <
< ![]() — правильна нерівність, як
— правильна нерівність, як
7 < х < 11, тобто х набуває одного із значень: 8, 9, 10;
2) 1![]() =
= ![]() ; 2
; 2![]() =
= ![]() , тому
, тому ![]() <
< ![]() <
< ![]() — правильна нерівність, якщо
— правильна нерівність, якщо
8 < х < 12, тобто х набуває одного із значень: 9, 10, 11.
№ 765. Один із способів розв'язання цього завдання — підібрати шукане число, підставити послідовні натуральні числа, починаючи з найменшого. Можна також запропонувати учням спочатку замість нерівностей спробувати розв'язати рівняння 1) ![]() = 2, 2)
= 2, 2) ![]() = а, а потім, використовуючи властивості ділення, знайти шукані числа.
= а, а потім, використовуючи властивості ділення, знайти шукані числа.
1) ![]() = 2, а = 10, якщо ділене збільшиться, то частка зменшиться, тобто шукані значення а задовольняють нерівності а > 10;
= 2, а = 10, якщо ділене збільшиться, то частка зменшиться, тобто шукані значення а задовольняють нерівності а > 10;
2) ![]() = а, а = 2, щоб частка збільшилась, ділене треба зменшити, тобто шукане натуральне число а задовольняє нерівність а < 2, отже, а = 1.
= а, а = 2, щоб частка збільшилась, ділене треба зменшити, тобто шукане натуральне число а задовольняє нерівність а < 2, отже, а = 1.
Задача 1.
Розв'язання.
Увесь маршрут — 1:
1) 1 – ![]() =
= ![]() — частина маршруту, що пройдена за II день;
— частина маршруту, що пройдена за II день;
2) 24 : 8 = 3 (km) складає ![]() маршруту;
маршруту;
 3) 3 · 15 = 45 (km) — увесь маршрут.
3) 3 · 15 = 45 (km) — увесь маршрут.
Відповідь. 45 км.
Задача 2.
Розв'язання.
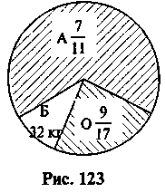
Остача — 1 (рис. 123)
1) 1 – ![]() =
= ![]() остачі складали банани;
остачі складали банани;
2) 32 : 8 = 4 (кг) ![]() – остачі;
– остачі;
3) 4 · 17 = 68 (кг) — остача;
4) маса фруктів — 1; 1 – ![]() =
= ![]() — частина, що є остачею;
— частина, що є остачею;
5) 68 : 4 = 17 (кг) ![]() усієї маси фруктів;
усієї маси фруктів;
6) 17 · 11 = 187 (кг) усього фруктів було привезено.
Відповідь. 187 кг.
Задача 3
1) х = 5![]() – 2
– 2![]() ; х = 4
; х = 4![]() – 2
– 2![]() ; х = 2
; х = 2![]() ;
;
2) х – 7![]() = 4
= 4![]() – 2
– 2![]() ; х – 7
; х – 7![]() = 1
= 1![]() ; х = 1
; х = 1![]() + 7
+ 7![]() ; х = 8
; х = 8![]() .
.
Задача 4. Бачимо, що у першому рядку ![]() числа — це 6, отже, число, що позначає круг 6 · 2 = 12; у другому рядку круг і
числа — це 6, отже, число, що позначає круг 6 · 2 = 12; у другому рядку круг і ![]() круга — 12 + 12 : 4 · 1 = 15.
круга — 12 + 12 : 4 · 1 = 15.
Отже, у третьому рядку два круга і ![]() круга відповідають числу:
круга відповідають числу:
12 + 12 + 12 : 4 · 3 або 12 · 3 – 12 : 4 = 33.
IV. Підсумок уроку
Вчитель підсумовує вивчення теми «Дробові числа» і наголошує, що наступний урок є узагальнюючим, присвяченим підготовці до контрольної роботи.
V. Домашнє завдання
п. 26, №№758; 764; 768; 1105(10), на повторення 828.


про публікацію авторської розробки
Додати розробку
