Розробка уроку на тему "Перпендикулярність прямої і площини"

Урок № 24

Тема: Перпендикулярність прямої і площини

Мета: формувати  поняття  прямої  перпендикулярної  до  площини, вивчити  ознаку  перпендикулярності  прямої  і  площини, вчити  учнів  розв’язувати  задачі  практичного  змісту, застосовуючи поняття перпендикулярності;

розвивати просторову уяву, логічне мислення;

виховувати чесність, відповідальність, культуру математичних записів та мови.

Тип уроку: засвоєння нових знань.

Обладнання: набір креслярських інструментів, підручники, план-конспект, роздатковий матеріал,  проектор, комп’ютер.

 

Хід уроку

І. Організаційний момент.

Перевірка присутніх.

 

ІI. Актуалізація опорних знань.

Взаємоопитування ланцюжком

(учень відповідає на запитання, потім ставить запитання наступному учневі і т.д)

1. Яким може бути взаємне розміщення двох прямих у просторі?

(Прямі у просторі можуть перетинатися, можуть бути паралельними або мимобіжними)

2. Які прямі у просторі називаються перпендикулярними?

(Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом)

3. Чому дорівнює градусна міра прямого кута?

(Градусна міра прямого кута дорівнює 90⁰)

4. Чи визначають площину дві перпендикулярні прямі? Чому?

(Так, дві перпендикулярні прямі визначають площину, бо за наслідком з аксіом стереометрії через дві прямі, що перетинаються, можна провести площину і до того ж тільки одну)

5. Яким може бути взаємне розміщення прямої і площини?

(Можливі три випадки взаємного розміщення прямої і площини: пряма лежить у площині, пряма і площина паралельні, пряма і площина перетинаються)

 

ІIІ. Повідомлення теми, мети і завдань уроку.

ІV. Мотивація навчальної діяльності.

Ми  живемо  у  стереометричних  фігурах, ми  будуємо  стереометричні  фігури, ми  користуємось  у  побуті  стереометричними  фігурами, тому  вивчати  стереометрію  потрібно  досконало, щоб  вміти  застосовувати  її  в житті.

 

Отже, для подальшого розв’язування задач нам необхідний теоретичний інструментарій, тобто означення і теореми, що визначають перпендикулярність прямої і площини.

Давайте на хвилинку повернемося в минуле і дізнаємося, хто з математиків працював над вивченням перпендикулярності прямої і площини.

Хвилинка історії.

V. Сприймання і усвідомлення нового матеріалу.

Давайте сформулюємо і запишемо означення прямої, перпендикулярної до площини.

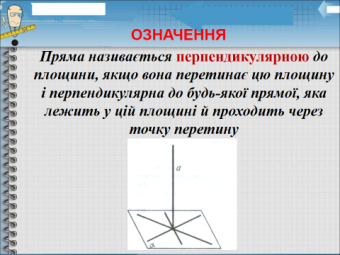
Приклад з шваброю.

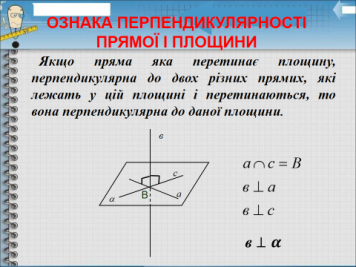
Давайте сформулюємо і запишемо ознаку перпендикулярності прямої і площини.

 

VІ. Застосування набутих знань.

 

Усні вправи.

 

 

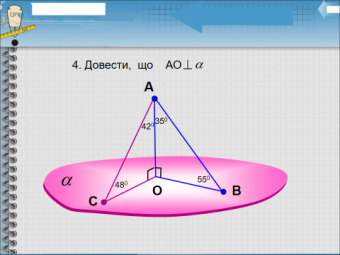
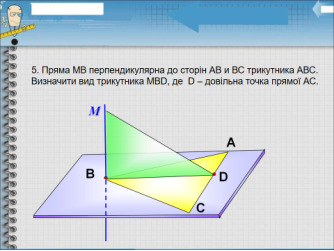
Задача «Заповни пропуски» (картки для учнів)

Телефонний провід завдовжки 15 м протягнуто від телефонного стовпа, де він прикріплений на висоті 8 м від поверхні Землі, до будинку, де його закріпили на висоті 20 м. Знайдіть відстань між будинком і стовпом, вважаючи, що провід не провисає.

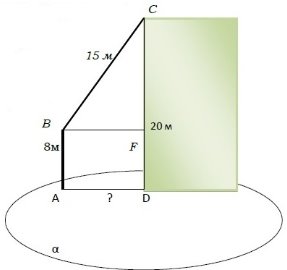Розв’язання:

Математична модель поверхні Землі – площина ____, а відстані 8 м і 20 м від поверхні Землі – прямі, що ___ площині ___.

За властивістю прямих і площин:

АВ ____СD. Проведемо BF___AD, тоді BF =____

і ΔBCF – _________________(<BFC =____°)

CF=____________.

За теоремою _____________:

BF² = ________________________________

BF = ±√ ____ = ±_____ (____ не задовольняє умову задачі).

Відповідь: відстань між будинком і стовпом _____м.

 

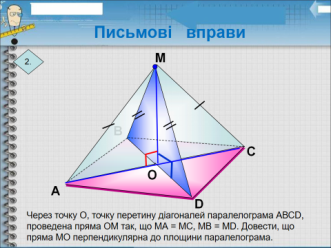
Задача на доведення

VІІ. Підсумки уроку.

Отже, можна зробити висновок, що люди вашої професії не можуть працювати без математики.

 

Виконання «Графічного диктанту» (фронтально).

Учні записують в робочих зошитах відповіді на запитання диктанту, користуючись символами «так»-∩, «ні»- ─, а потім здійснюють самоперевірку за ключем – відповіддю.

1. З даної точки до даної площини можна провести перпендикуляр, і тільки один.
2. Дві прямі називаються перпендикулярними, якщо вони перетинаються.
3. За теоремою Піфагора: у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
4. Щоб пряма була перпендикулярною до площини достатньо, щоб вона була перпендикулярна до однієї прямої в цій площині.
5. Перпендикулярні прямі утворюють кут 90⁰.

Ключ: .

 

VІІІ. Домашнє завдання.

 

Скласти задачу прикладного змісту на застосування перпендикулярності прямої і площини.