Розробка уроку на тему "Площа. Площа прямокутника."

Тема. Площа. Площа прямокутника.

Мета: ввести поняття одиниці виміру площі; формувати навички ро­боти з різними одиницями вимірювання площ та обчислення площі пря­мокутника і квадрата.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця «Площа. Площа прямокутника».

Хід уроку

І. Перевірка домашнього завдання

Математичний диктант

Варіант 1 [2]

1. Вираз 17² [14³] запишіть у вигляді добутку.
2. Вираз 26³ [23² ] запишіть у вигляді добутку.
3. Запишіть будь-який вираз, який можна записати у вигляді квадрата [куба].
4. Обчисліть 22² [7⁵].
5. Обчисліть 6³ [11²].
6. Який вираз отримаємо, якщо 49² помножити на 49 [53² помножити на 53]?
7. Чому дорівнює сума квадратів чисел 3 і 4 [куб чисел 2 і 3]?

II. Актуалізація опорних знань

Усні вправи

1. Скільки:

1) сантиметрів міститься в: 1 дм, 1 м 3 дм, 5 м 2 дм, 40 мм?

2) метрів міститься в: 1 км, 2 км 418 м, 4 км 16 м, 800 см?

2. Яка з фігур на рисунку 82 зайва?

3. Знайдіть периметр:

1) прямокутника, ширина якого 11 см, а довжина в 3 рази більша;

2) квадрата, якщо довжина його сторони дорівнює З² см?

4. На скільки квадратів зі стороною 1 см можна розбити прямокутник зі
   сторонами:

1) 3 см і 4 см; 2) 30 мм і 4 см; 3) а см і 4 см; 4) а см і 6см?

5. Знайдіть пропущені числа в ланцюжку:

III. Систематизація раніше набутих знань і засвоєння нових знань

 Оскільки з поняттям площі фігур та формулами для обчислення площ прямокутника й квадрата учні ознайомились у початковій школі, ос­новна мета уроку:

1) роз'яснити учням, що для вимірювання будь-яких величин (довжини, градусної міри, площі і таке інше) в математиці існує єдиний підхід — спочатку домовлятися про одиниці виміру (одиничний відрізок, оди­ничний кут, одиничний квадрат);

2) сформулювати основні властивості площ:

• якщо фігури рівні, то їхні площі рівні;
• площа квадрата з одиничною стороною — одиничний квадрат;
• якщо фігуру Поділити на частини, то сума площ цих частин дорівнює площі фігури;

3) встановити зв'язок між відомими одиницями вимірювання площ і новими (1 ар, 1 га);

4) довести формулу S = ab для натуральних чисел а і b.

III. Формування вмінь, закріплення знань

На закріплення матеріалу запропонувати учням розв'язати декілька завдань.

Завдання 1

1. Яка з чотирьох фігур, зображених нарис. 83 зліва, дорівнює фігурі, зображеній на цьому рисунку справа?

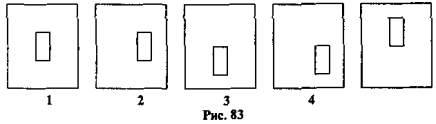
Завдання 2

Заповнити пропущені в ланцюжку величини:

Завдання 3

Обчислити площу прямокутника зі сторонами:

1) 14 см і 8 см; 2) 14 см і 80 мм; 3) 14 см і друга в 2 рази менша.

Завдання 4

Обчислити площу квадрата, якщо:

1.   сторона 7 дм;
2.   периметр 24 см;
3.   його периметр дорівнює периметру прямокутника зі сторонами 10 і 12 см.

Після виконання завдань 1-3 учням пропонується виконати вправи з підручника.

№ 582. Розв'язуємо за допомогою рівнянням Р = 162 дм — периметр; Ь= 47 дм — одна зі сторін;

Р = (а + b); 162 = 2 · (а + 47); а = 34дм.

S = ab; S = 47 · 34 = 1598 дм².

№ 585. Розв'язуємо рівняння Р = 4 м 8 дм, ширина — х дм, довжина 5х дм. Периметр 2(х + 5х)(дм) дорівнює 48 дм, тому 2(х + 5х) = 48; 12х = 48; х = 4,   отже,   ширина   8дм,   довжина   8 · 5 = 40 дм,  

площа  S = ab; S = 8 · 40 = 320 дм².

Відповідь. 320 дм².

№ 587. Пояснити, як легко виконувати перехід від однієї одиниці площі до іншої за допомогою ланцюжка (див. завдання 2).

IV. Підсумок уроку

V. Домашнє завдання

п. 20, №№ 577 (усно); 581; 583; 586; 588.