Розробка уроку на тему "Прямокутник"
Тема. Прямокутник
Мета: сформувати в учнів уявлення про прямокутник як один із видів паралелограма; розглянути властивості та ознаки прямокутника; сформувати вміння й навички застосовувати властивості та ознаки прямокутника під час розв'язування задач.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Прямокутник».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Учитель збирає зошити учнів із виконаною домашньою самостійною роботою на перевірку. У разі потреби на цьому етапі проводиться стислий аналіз виконаних завдань, та учні, які припустилися великої кількості помилок, отримують завдання для корекційної роботи.
III. Формулювання мети і завдань уроку
З метою створення умов для усвідомленого сприйняття учнями матеріалу уроку пропонуємо їм розв'язати логічну вправу.
Порівняйте фігури на рисунку 1 (за різними критеріями). Яка із фігур «зайва»?
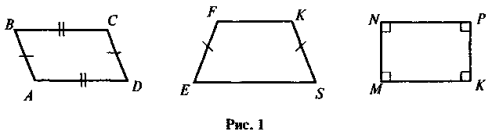
Після успішного виконання завдань (зрозуміло, що «зайвим» є чотирикутник EFKS, у якого на відміну від двох інших чотирикутників є лише дві паралельні сторони) учитель звертає увагу учнів на той факт, що паралелограм MNPK є особливим випадком паралелограма, бо, крім паралельності протилежних сторін, має прямі кути. Таким чином, виділяється новий об'єкт, вивчення якого за загальною схемою і становить основну дидактичну мету.
IV. Актуалізація опорних знань та вмінь
Для свідомого розуміння та подальшого засвоєння учнями змісту означення, властивостей та ознак прямокутника слід активізувати знання і вміння учнів щодо означення, властивостей та ознак паралелограма; означення прямокутного трикутника та ознак рівності прямокутних трикутників; означення, властивостей кутів та ознак рівнобедреного трикутника.
Виконання усних вправ за готовими рисунками
|
1 |
|
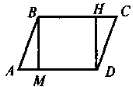
Дано: Довести: АМВН – паралелограмм |
|
2 |
|
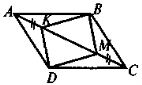
Дано: ABCD — паралелограм, АК = СМ. Довести: DKBM — паралелограм. |
|
3 |
|
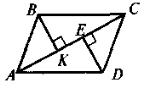
Дано: ABCD — паралелограм, BM |
|
4 |
|
Дано: ABCD — паралелограм, ВК Довести: ВК = DE |
|
5 |
|
Дано: AD = DC = BD.
Довести: |
V. Засвоєння знань
План вивчення нового матеріалу
- Означення прямокутника.
- Властивості прямокутника.
- Ознаки прямокутника.
План вивчення поняття прямокутника за новим підручником відповідає уявленню учнів про план вивчення будь-якої геометричної фігури (відношення між фігурами), вміщеної в таблиці 1 (див. Геометрія в таблицях Є. П. Неліна), а саме: спочатку вивчається означення прямокутника, далі вивчається питання про його властивості, після чого формулюються ознаки прямокутника.
Означення прямокутника формулюється традиційно. Цілком логічно з означення випливає виконання загальних властивостей паралелограма для будь-якого прямокутника (тому властивості протилежних сторін, протилежних кутів та властивості відрізків, на які ділиться діагональ прямокутника, а також властивості бісектрис прямокутника формулюються без доведення).
Але надалі учні мають усвідомити, що під час вивчення фігури, що є «особливим» видом паралелограма, слід також розглянути властивості, які притаманні тільки цим фігурам. (Вивчаючи ромб та квадрат, ми будемо дотримуватися цієї ж логіки розгляду властивостей.)
Тому далі вивчається теорема про властивість діагоналей прямокутника, яка доводиться традиційно через рівність прямокутних трикутників. Що стосується інших властивостей прямокутника, які корисно було б додатково розглянути з учнями (оскільки вони досить часто використовуються у розв'язуванні задач, особливо в стереометрії), то таких можна виділити дві:
- відрізок, що з'єднує середину сторони прямокутника з точкою перетину діагоналей, перпендикулярний до цієї сторони і дорівнює половині суміжної сторони прямокутника (ця властивість використовується під час розв'язування задач, в яких мова йде про відстань від точки перетину діагоналей прямокутника до його сторони);
- кут між діагоналями прямокутника вдвічі більший за кут між діагоналями та більшою стороною прямокутника.
Доведення зазначених властивостей діагоналей прямокутника є досить простими, тому їх можна розглянути як додаткові задачі, а потім здобуті властивості зафіксувати в зошитах учнів як опорні факти.
Серед ознак прямокутника, які викладено в новому підручнику, слід звернути увагу як на ознаку, що традиційно вивчалась у 8 класі (ознака прямокутника за рівністю діагоналей), так і на ознаки, які сформульовані у вигляді опорних задач.
Опорні задачі (ознаки прямокутника)
- Якщо всі кути чотирикутника прямі, то цей чотирикутник — прямокутник.
- Якщо один із кутів паралелограма прямий, то цей паралелограм є прямокутником.
Звернімо увагу учнів на те, що під час вивчення питання про властивість діагоналей прямокутника та ознаку прямокутника за рівністю його діагоналей використовується термінологія, вивчена на попередньому уроці (необхідна і достатня умови, критерій геометричного об'єкта).
Повний перелік тверджень, що стосуються прямокутника, які бажано вивчити з восьмикласниками, міститься в конспекті «Прямокутник».
|
Конспект 3 |
||
|
|
Прямокутник Означення. Паралелограм, усі кути якого прямі, називається прямокутником |
|
|
|
Властивості |
Ознаки |
|
|
1. Усі властивості
2. Якщо ABCD - |
1. Якщо ABCD — паралелограм і Якщо ABCD — паралелограм і АС = BD, то ABCD — прямокутник. (Якщо діагоналі паралелограма рівні, то цей паралелограм — прямокутник) |
|
3. Якщо ABCD — прямокутник, (AD > CD), AC і BD — діагоналі, то |
|
|
|
|
4. Якщо ABCD — прямокутник і точка М — середина ВС, то ОМ
ОМ = |
|
|
|
(Відрізок, що з'єднує середину сторони прямокутника з точкою перетину діагоналей, перпендикулярний до цієї сторони і дорівнює половині суміжної сторони) |
|
VII. Формування первинних умінь
З метою закріплення знань учнів щодо означення, властивостей та ознак прямокутника спочатку доцільно розв'язати усні задачі.
Виконання усних вправ
- У прямокутнику ABCD А В = 8 см, ВС = 5 см. Знайдіть:
а) відстань від точки С до сторони AD;
б) відстань між прямими АВ і CD.
-
 Чи може діагональ прямокутника дорівнювати його стороні? Чи може діагональ ромба дорівнювати його стороні?
Чи може діагональ прямокутника дорівнювати його стороні? Чи може діагональ ромба дорівнювати його стороні?
-
а) Укажіть (див. рис. 2) відрізки, кути,
трикутники.
б) ![]() AOD = 142°. Знайдіть
AOD = 142°. Знайдіть ![]() OCD і
OCD і ![]() OBC.
OBC.
в) РВОС = 16 см, АС · BD = 100. Знайдіть AD.
-
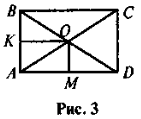 За рисунком 3 розв'яжіть задачі:
За рисунком 3 розв'яжіть задачі:
а) КО = 4 см, ОМ = 2 см. Знайдіть PABCD.
б) ![]() AOD = 120°, BD = 2 см. Знайдіть РОВС.
AOD = 120°, BD = 2 см. Знайдіть РОВС.
-
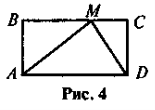
У прямокутнику ABCD (рис. 4)
 BAM =
BAM = DAM,
DAM,  MDC = 30°, АВ = 1, ВС = 3. Знайдіть PABМD.
MDC = 30°, АВ = 1, ВС = 3. Знайдіть PABМD.
 Після закріплення знань означення, властивостей та ознак прямокутника доцільно розв'язати типові задачі на застосування цих знань.
Після закріплення знань означення, властивостей та ознак прямокутника доцільно розв'язати типові задачі на застосування цих знань.
Виконання письмових вправ
- Знайдіть периметр прямокутника ABCD, якщо АС =15 см, а периметр трикутника ABC дорівнює 36 см.
-
У прямокутнику ABCD
 BAC = 65°. Знайдіть кут між діагоналями прямокутника.
BAC = 65°. Знайдіть кут між діагоналями прямокутника.
-
Діагоналі прямокутника ABCD перетинаються в точці О, причому
 COD = 60°, CD = 8 см. Знайдіть довжину діагоналі.
COD = 60°, CD = 8 см. Знайдіть довжину діагоналі.
- Точка перетину діагоналей прямокутника віддалена від двох його сторін на 3 см і 4 см. Знайдіть периметр прямокутника.
VII. Підсумки уроку
Який з чотирикутників не є прямокутником?
1) Чотирикутник, у якого протилежні сторони паралельні і один кут прямій.
2) Паралелограм, який має прямий кут.
3) Паралелограм, у якого діагоналі рівні.
4) Чотирикутник, у якого діагоналі перпендикулярні і діляться у точках перетину навпіл.
VIII. Домашнє завдання
Вивчити зміст означення, властивостей та ознак прямокутника (див. конспект).
Розв'язати задачі.
- Знайдіть сторони прямокутника, периметр якого дорівнює 36 см, а одна сторона вдвічі більша за іншу.
- Діагоналі прямокутника перетинаються під кутом 80°. Знайдіть кути, на які діагональ ділить кут прямокутника.
- Бісектриса кута прямокутника ділиться його сторону завдовжки 12 см навпіл. Знайдіть периметр прямокутника.
-
а) ВН
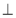 АС,
АС,  ACD = 60°, ОН = 5 см (рис. 5). Знайдіть АВ і BD.
ACD = 60°, ОН = 5 см (рис. 5). Знайдіть АВ і BD.
 б) ВН
б) ВН![]() АС, ВН = 3 см, BD = 12 см. Знайдіть
АС, ВН = 3 см, BD = 12 см. Знайдіть ![]() CAD.
CAD.
Повторити означення, властивості кутів та ознаки рівнобедреного трикутника.


про публікацію авторської розробки
Додати розробку