Розробка уроку на тему "Співвідношення між тригонометричними функціями одного й того самого аргументу"
Державний навчальний заклад
«Мукачівський центр професійно-технічної освіти»
Розробка уроку
з математики
на тему
«Співвідношення між тригонометричними функціями одного й того самого аргументу»
Виконала:
викладач математики
Петах Вікторія Йосипівна
Мукачево 2017 р.
Тема: Основні співвідношення між тригонометричними функціями одного аргументу
Мета:
- освітня: узагальнити, систематизувати та поглибити знання учнів про тригонометричні функції;
- розвиваюча: розвивати вміння учнів застосовувати отримані знання для розв΄язування вправ та спрощення тригонометричних виразів; сприяти формуванню навичок самостійної роботи й роботи в команді; розвитку навичок усного мовлення, уміння правильно вести діалог й аргументувати свої дії.
- виховна: виховувати інтерес до математики, спонукати до пізнавальної діяльності.
Форми роботи: колективна, групова, індивідуальна.
Тип уроку: узагальнення та систематизація знань, умінь і навичок.
Обладнання: Ноутбук, презентація у Power Point, картки-завдання для гри “Естафета”, кросворд.
Епіграф: «Знання лише тоді знання, коли воно отримане
зусиллям розуму, а не пам’яті»
Л.М.Толстой.
Хід уроку
І. Організація класу.
Проводжу перевірку присутніх на уроці учнів.
ІІ. Повідомлення теми і мети уроку
Учитель. Які асоціації викликає у вас слово «урок»?
У —успіх,
Р —радість,
О — обдарованість,
К — компетентність.
Сподіваюся, що сьогодні на нас чекає і успіх, і радість. Ви зможете продемонструвати власну обдарованість і компетентність.
Досягти успіху можна лише тоді, коли є певна мета, тому сформулюємо тему і мету нашого уроку.
На слайді з’являється тема уроку
Викладач. Тема нашого уроку «Співвідношення між тригонометричними функціями одного й того самого аргументу». Це означає, що на цьому занятті ми пригадаємо основну тригонометричну тотожність, а також ряд формул, які пов΄язують дані тригонометричні функції одного аргументу, навчимося використовувати дані співвідношення при розв΄язуванні вправ та задач.
Видатний письменник Л.М. Толстой говорив: «Знання лише тоді знання, коли воно отримане зусиллям розуму, а не пам’яті». От і ми на сьогоднішньому відкритому уроці будемо тренувати свою розумову діяльність.
ІІІ. Актуалізація та опорних знань учнів
1. Усна розминка «Алгебраїчний футбол»
Клас поділяється на 3 групи
Викладач. Вашу готовність до сьогоднішнього уроку давайте перевіримо за допомогою усної розминки «Алгебраїчний футбол».
Викладач задає запитання одному з членів команди, той відповідає передає право відповіді будь-якому члену другої команди. У випадку, якщо учень відповідає не правильно, то право відповіді переходить учневі іншої команди.
- Назвати основні тригонометричні функції.
- Що називається синусом кута через одиничне коло?
- Що називається косинусом кута через коло довільного радіуса?
- Що називається тангенсом кута через прямокутний трикутник?
- Що називається котангенсом кута через одиничне коло?
- В чому вимірюються кути?
- Як називається коло радіуса 1 з центром у початку координат?
- В яких чвертях знаки синуса і косинуса протилежні?
- Який знак має тангенс в IV чверті?
- Кутом якої чверті є кут 150?
- В яких чвертях котангенс від’ємний?
- В яких чвертях знаки синуса і косинуса співпадають?
написання графічного диктанту.
- «Графічний диктант»
В якості перевірки домашнього завдання та з метою актуалізації опорних знань учні виконують завдання графічного диктанту:
- Кут 390-кут ___ чверті (1 чверть);
- tg(-110)____0 (>);
-
Обчислити
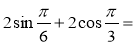
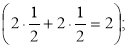
- Відомо, що sin та cos від’ємні. Чи може кут α бути кутом IV чверті? (ні)
- Відомо, cos β<0, а ctg β>0. Кутом якої чверті є кут β? (3 чверть)
-
Чи правильно, що
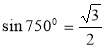 ? (ні--
? (ні--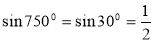 )
)
По закінченню диктанту учні обмінюються листочками з відповідями з сусідами по парті та разом з учителем перевіряють свої роботи.
-
 Усне опитування «Додатковий бал»
Усне опитування «Додатковий бал»
Отже,
- що таке тригонометрія?
- де використовується тригонометрія?
Учень 1. Тригонометрія виникла із практичних потреб людини. З її допомогою можна визначити відстань до недоступних предметів й, взагалі, істотно спрощувати процес геодезичної зйомки місцевості для складання географічних карт.
Учень 2. Тригонометричні функції широко застосовуються в математиці, фізиці, техніці. Багато процесів, такі як коливання струни, маятника, звукові коливання, напруга в ланцюзі змінного струму й т.д., описуються за допомогою тригонометричних функцій.
-
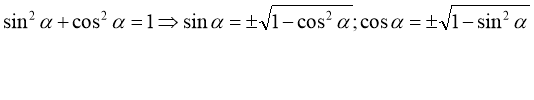
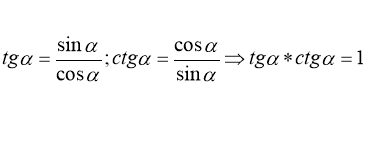 Запишіть основні співвідношення між тригонометричними функціями одного аргументу.
Запишіть основні співвідношення між тригонометричними функціями одного аргументу.
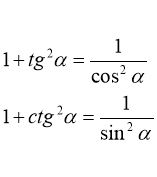
IV. Відпрацювання вмінь та навичок
- Конкурс «Встанови відповідність»
Учні з допомогою вчителя по черзі, користуючись формулами, встановлюють відповідність між тригонометричними виразами записуючи відповідні записи на дошці та в зошитах.
|
|
А) |
|
|
|
|
3) |
|
|
4) |
Г) |
|
5) |
|
|
6) |
Е) tg |
Відповідь: 1-Г; 2-В; 3-Д; 4-Б; 5-А;6-Е.
- «Командні змагання»
Виконання письмових вправ учнями з кожної команди на дошці. За правильність виконання 5 балів+2 бали за швидкість.
1. Знайдіть значення тригонометричних функцій аргументу ![]() , якщо:
, якщо:
а) ![]() ;
;
б) 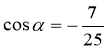 і
і ![]()
в) ![]() і
і ![]()
2. Спростіть вираз:
а) ![]()
б) 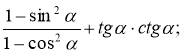
в) 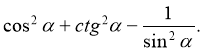
V. Осмислення, узагальнення й систематизація знань
Естафета «Ключове слово»
Всі ви знаєте, що таке естафета з уроків фізкультури, але сьогодні ми проведемо математичну естафету. Зараз я розповім правила нашої гри. Як і в кожній естафеті, у нас буде своя естафетна паличка – аркуш із завданням, тобто наступний гравець зможе перейняти на себе естафету лише після того, як попередній віддасть йому цю «естафетну паличку». За правильність виконання завдання по 2 бали+ 2 бали за швидкість і правильність ключового слова.
Команда “Синус”
-
Виразіть величину кута
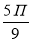 у градусах:
у градусах:
|
Б |
В |
Г |
Д |
|
80º |
60º |
50º |
100º |
-
Знайдіть значення виразу:
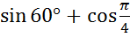
|
П |
Р |
С |
Т |
|
|
|
|
|
-
Спростіть вираз:
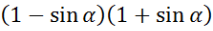 :
:
|
А |
О |
К |
Л |
|
|
|
|
|
-
Знайдіть значення виразу tg
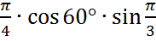 :
:
|
М |
Н |
Е |
Г |
|
1 |
|
2 |
|
Допоміжні літери: У, Р
|
|
|
|
|
|
|
Команда “Косинус”
-
Виразіть величину кута
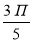 у градусах:
у градусах:
|
А |
Б |
В |
Г |
|
108º |
150º |
36º |
72º |
-
Знайдіть значення виразу:
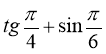
|
Г |
Д |
З |
Е |
|
|
|
1 |
|
-
Спростіть вираз:

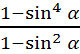
|
С |
П |
О |
І |
|
|
|
|
|
- Знайдіть значення виразу:

|
К |
Н |
Л |
М |
|
1 |
|
2 |
|
Допоміжні літери: А, Р
|
|
|
|
|
|
|
Команда “Тангенс”
-
Виразіть величину кута
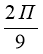 у градусах:
у градусах:
|
Б |
И |
В |
К |
|
60º |
72º |
50º |
40º |
-
Знайдіть значення виразу:
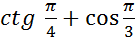
|
П |
Р |
С |
Т |
|
|
1,5 |
|
|
-
Спростіть вираз:
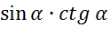
|
А |
О |
Д |
Л |
|
|
|
|
|
-
Знайдіть значення виразу:
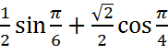
|
Н |
М |
Е |
Г |
|
|
|
2 |
|
Допоміжні літери: Ь, І
|
|
|
|
|
|
|
VI. Підведення підсумків заняття.
Викладач. На сьогоднішньому занятті мі розширили наші знання про тригонометричні функції, познайомились з формулами, що зв'язують тригонометричні функції одного аргументу, навчилися застосовувати отримані знання при розв΄язуванні вправ.
А зараз повторимо найголовніше у вигляді кросворду:
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КРОСВОРД
- Рівність двох виразів.
- Плоский кут, утворений 2 радіусами, такий, що довжина дуги між ними точно дорівнює радіусу.
- Відношення абсциси «х» точки одиничного кола до радіуса.
- Відношення ординати «у» точки одиничного кола до його абсциси «х».
- Коло радіуса 1 з центром у точці О(0;0).
- Відношення абсциси «х» точки одиничного кола до його ординати «у».
- Інструмент для вимірювання кутів.
- Незалежна змінна тригонометричної функції.
- Як називається кут, утворений двома радіусами кола?
- Частина кола, на яку поділяють одиничне коло вісь абсцис та ординат.
- Трикутник, один з кутів якого дорівнює 90.
- Залежність, при якій кожному значенню незалежної змінної ставиться у відповідність єдине значення залежної змінної.
- Чому дорівнює sin 90?
VII. Домашнє завдання
- Спростити вираз:
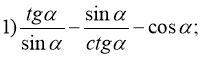
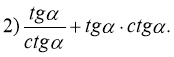
2) Обчислити значення інших тригонометричних функцій за даним значенням однієї з них:
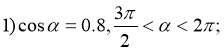
![]() .
.
1


про публікацію авторської розробки
Додати розробку